King's Path

题目描述

There are $ n $ cities and $ n-1 $ two-way roads in Treeland. Each road connects a pair of different cities. From any city you can drive to any other, moving only along the roads. Cities are numbered from $ 1 $ to $ n $ . Yes, of course, you recognized an undirected tree in this description. There is exactly one flag in each city, in the $ i $ -th city the flag color is $ c_i $ . The colors of the flags in different cities may be the same. If the King travels along the route $ [u_1, u_2, u_3, \dots, u_k] $ , then this means that he starts in the city $ u_1 $ , then moves to the city $ u_2 $ ( $ u_2 $ is connected by road with $ u_1 $ ), then from $ u_2 $ to $ u_3 $ ( $ u_3 $ is connected by road to $ u_2 $ ), and so on until he arrives in the city of $ u_k $ . It is possible that during this route the King will visit the same city more than once. In other words, the route $ [u_1, u_2, u_3, \dots, u_k] $ does not necessarily consist of different cities. In terms of graph theory — the King moves from $ u_1 $ to $ u_k $ along some path $ [u_1, u_2, u_3, \dots, u_k] $ , which is not necessarily simple (for all $ j $ from $ 1 $ to $ k-1 $ of the city $ u_j $ and $ u_{j+1} $ are connected by road). When the King moves from one city to another, city heads exchange flags as a sign of their friendship. 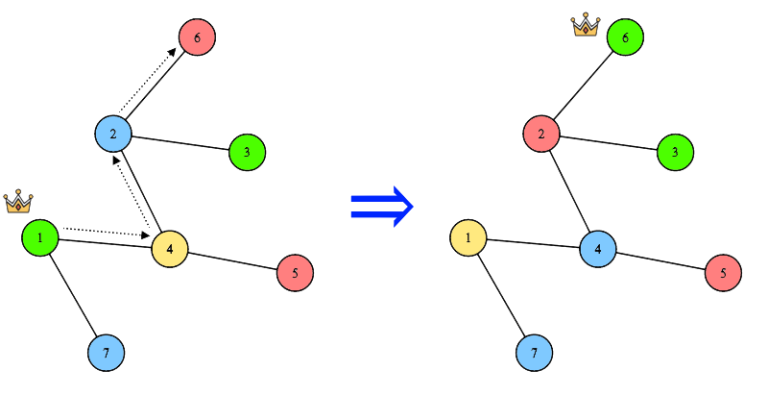Example of moving the King along the route $ [1, 4, 2, 6] $ . The color of the vertex matches the color of the flag at that vertex.For aesthetic reasons, the King wants the flag color in the city $ i $ to be equal to $ d_i $ for all $ i $ from $ 1 $ to $ n $ . Determine whether the King can choose some route and drive along it so that for each city the flag color in it turns out to be equal to the desired color $ d_i $ . Note that the King can choose (and drive) exactly one route. If yes, find the shortest possible route for the King. If the initial colors of the flags already match the King's requirements (i.e. $ c_i=d_i $ for all $ i $ ), then consider that the King makes a route of length $ k=0 $ .

输入输出格式

输入格式

The first line contains an integer $ t $ ( $ 1 \le t \le 10^5 $ ) — the number of test cases to solve. The following are the cases. Each case begins with a line containing an integer $ n $ ( $ 2 \le n \le 2\cdot10^5 $ ) — the number of cities in Treeland. The following is a line of $ n $ integers $ c_1, c_2, \dots, c_n $ ( $ 1 \le c_i \le 10^6 $ ), where $ c_i $ denotes the color of the flag at the $ i $ -th vertex before the King's journey. The following is a line of $ n $ integers $ d_1, d_2, \dots, d_n $ ( $ 1 \le d_i \le 10^6 $ ), where $ d_i $ denotes the required flag color at the $ i $ -th vertex after the completion of the King's journey. Further, in the $ n-1 $ line, the Treeland's roads are listed. Each road is given by a line containing two integers $ x_j, y_j $ ( $ 1 \le x_j, y_j \le n $ ) — numbers of cities that are connected by the $ j $ th road. It is guaranteed that from every city you can get to any other by road (in other words, the system of cities and roads forms an undirected tree). The sum of all $ n $ values ​​for all cases in one test does not exceed $ 2\cdot10^5 $ .

输出格式

Print the answers to all cases in the order of their appearance in the input data. Each answer must begin with a line containing "Yes" (in the case of a positive answer) or "No" (in the case that the required route does not exist). In the case of a positive answer, the following line must contain an integer $ k $ — the number of cities in the shortest possible route of the King. The next line should contain the required route $ u_1, u_2, \dots, u_k $ ( $ 1 \le u_i \le n $ ). You can skip the line if $ k=0 $ .

输入输出样例

输入样例 #1

1
7
2 3 2 7 1 1 3
7 1 2 3 1 2 3
1 7
4 1
2 6
2 3
2 4
5 4

输出样例 #1

Yes
4
1 4 2 6 

输入样例 #2

1
5
1 2 2 2 2
2 2 2 2 1
1 2
2 3
3 4
4 5

输出样例 #2

Yes
5
1 2 3 4 5 

输入样例 #3

3
4
10 20 10 20
20 10 20 10
1 2
1 3
1 4
2
1000000 1000000
1000000 1000000
1 2
10
4 2 2 4 2 4 1 2 3 4
4 2 4 4 3 2 1 2 4 2
5 8
6 9
10 5
1 10
7 10
3 4
5 9
3 10
2 4

输出样例 #3

No
Yes
0
Yes
5
3 10 5 9 6