Fridge Lockers

题意翻译

## 题意翻译 现在有$n$人，每人都拥有1个冰箱。现提供$m$条铁链，每条铁链可以连接两个冰箱，且只有这两个冰箱的主人可以解锁这条铁链。 只有冰箱上所有铁链都被解锁后，才能打开这个冰箱，如果一个冰箱被铁链加固后只有它的主人可以独自打开它，那么我们称这个冰箱是“私有的”。 另外，如果只有2个冰箱，那么无论有多少条铁链，两个冰箱都不是“私有的”，因为这两个人都可以独自打开对方的冰箱。 在图例中有4个冰箱和5条铁链，所有冰箱都是“私有的”。1号冰箱的主人可以解锁连接1-2和连接1-4的铁链，1号冰箱只能被它的主人独自打开，或者被2号和4号同时打开。 每个冰箱都有一个重量，记为$a_1,a_2,a_3,\ldots,a_n$。如果要给u号和v号冰箱用铁链加固，需要花费$a_u+a_v$元。两个冰箱之间可以有多条铁链加固。 请求出，在将$m$条铁链全部被使用后，所有冰箱是否可能均为“私有的”，如果可能，那么求出最小花费是多少。 ## 输入格式 **每个测试点包含多组测试数据** 第一行输入数据组数$T$($1 \le T \le 10$)，接下来输入$T$组数据，每组数据格式如下： 第一行包含两个正整数$n,m$($2 \le n \le 1000,1 \le m \le n $)，分别代表人数和铁链数量。 第二行包含$n$个整数$a_1,a_2,a_3,\ldots,a_n$($0 \le a_i \le 1000$)，代表每个冰箱的重量。 ## 输出格式 对于每组测试数据： - 如果不能使每个冰箱都是“私有的”，输出-1。 - 否则，输出一个整数$c$，代表最小花费。接下来每行，对于第$i$行，输出第$i$条铁链连接的两个冰箱。两个冰箱之间可以有任意多的铁链相连。 如果答案不唯一，输出任意一组。

题目描述

Hanh lives in a shared apartment. There are $ n $ people (including Hanh) living there, each has a private fridge. $ n $ fridges are secured by several steel chains. Each steel chain connects two different fridges and is protected by a digital lock. The owner of a fridge knows passcodes of all chains connected to it. A fridge can be open only if all chains connected to it are unlocked. For example, if a fridge has no chains connected to it at all, then any of $ n $ people can open it. 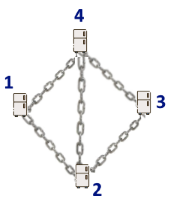For exampe, in the picture there are $ n=4 $ people and $ 5 $ chains. The first person knows passcodes of two chains: $ 1-4 $ and $ 1-2 $ . The fridge $ 1 $ can be open by its owner (the person $ 1 $ ), also two people $ 2 $ and $ 4 $ (acting together) can open it.The weights of these fridges are $ a_1, a_2, \ldots, a_n $ . To make a steel chain connecting fridges $ u $ and $ v $ , you have to pay $ a_u + a_v $ dollars. Note that the landlord allows you to create multiple chains connecting the same pair of fridges. Hanh's apartment landlord asks you to create exactly $ m $ steel chains so that all fridges are private. A fridge is private if and only if, among $ n $ people living in the apartment, only the owner can open it (i.e. no other person acting alone can do it). In other words, the fridge $ i $ is not private if there exists the person $ j $ ( $ i \ne j $ ) that the person $ j $ can open the fridge $ i $ . For example, in the picture all the fridges are private. On the other hand, if there are $ n=2 $ fridges and only one chain (which connects them) then both fridges are not private (both fridges can be open not only by its owner but also by another person). Of course, the landlord wants to minimize the total cost of all steel chains to fulfill his request. Determine whether there exists any way to make exactly $ m $ chains, and if yes, output any solution that minimizes the total cost.

输入输出格式

输入格式

Each test contains multiple test cases. The first line contains the number of test cases $ T $ ( $ 1 \le T \le 10 $ ). Then the descriptions of the test cases follow. The first line of each test case contains two integers $ n $ , $ m $ ( $ 2 \le n \le 1000 $ , $ 1 \le m \le n $ ) — the number of people living in Hanh's apartment and the number of steel chains that the landlord requires, respectively. The second line of each test case contains $ n $ integers $ a_1, a_2, \ldots, a_n $ ( $ 0 \le a_i \le 10^4 $ ) — weights of all fridges.

输出格式

For each test case: - If there is no solution, print a single integer $ -1 $ . - Otherwise, print a single integer $ c $ — the minimum total cost. The $ i $ -th of the next $ m $ lines contains two integers $ u_i $ and $ v_i $ ( $ 1 \le u_i, v_i \le n $ , $ u_i \ne v_i $ ), meaning that the $ i $ -th steel chain connects fridges $ u_i $ and $ v_i $ . An arbitrary number of chains can be between a pair of fridges. If there are multiple answers, print any.

输入输出样例

输入样例 #1

3
4 4
1 1 1 1
3 1
1 2 3
3 3
1 2 3

输出样例 #1

8
1 2
4 3
3 2
4 1
-1
12
3 2
1 2
3 1