306903: CF1268B. Domino for Young
Memory Limit:256 MB
Time Limit:3 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Domino for Young
题意翻译
给出一个不规则的网格。共 $n$ 列,每列有 $a_i$ 个格子。现在要将 $1 \times 2$ 的骨牌不重叠的覆盖在网格上,求最多能放的骨牌数量。 网格满足条件 $a_1\geq a_2\geq \ldots \geq a_n\geq 1$ .题目描述
You are given a Young diagram. Given diagram is a histogram with $ n $ columns of lengths $ a_1, a_2, \ldots, a_n $ ( $ a_1 \geq a_2 \geq \ldots \geq a_n \geq 1 $ ). 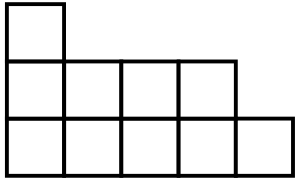Young diagram for $ a=[3,2,2,2,1] $ .Your goal is to find the largest number of non-overlapping dominos that you can draw inside of this histogram, a domino is a $ 1 \times 2 $ or $ 2 \times 1 $ rectangle.输入输出格式
输入格式
The first line of input contain one integer $ n $ ( $ 1 \leq n \leq 300\,000 $ ): the number of columns in the given histogram. The next line of input contains $ n $ integers $ a_1, a_2, \ldots, a_n $ ( $ 1 \leq a_i \leq 300\,000, a_i \geq a_{i+1} $ ): the lengths of columns.
输出格式
Output one integer: the largest number of non-overlapping dominos that you can draw inside of the given Young diagram.
输入输出样例
输入样例 #1
5
3 2 2 2 1
输出样例 #1
4