307162: CF1312A. Two Regular Polygons
Memory Limit:256 MB
Time Limit:1 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Two Regular Polygons
题意翻译
题目大意: - 有一个正凸多边形,有 $n$ 条边。 - 构造另一个有 $m$ 条边的正凸多边形,使得这个多边形的中心与给定的正多边形的中心重合,且构造的正多边形的顶点都在给定的正多边形的顶点上。 - 判断可不可能构造出这样的多边形。 输入输出: - 共 $t$ 组,每组两个正整数 $n,m$。 - 对于每一组输入,输出"YES"或"NO",作为应答(没有双引号)。 数据范围: - $1 \le t \le 10^4$ - $ 3 \le m < n \le 100$题目描述
You are given two integers $ n $ and $ m $ ( $ m < n $ ). Consider a convex regular polygon of $ n $ vertices. Recall that a regular polygon is a polygon that is equiangular (all angles are equal in measure) and equilateral (all sides have the same length). 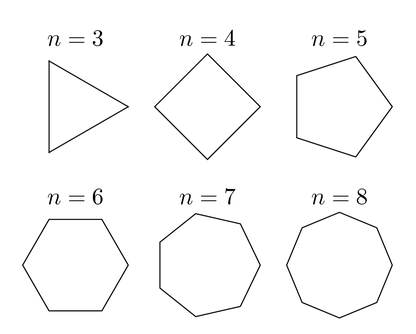 Examples of convex regular polygons Your task is to say if it is possible to build another convex regular polygon with $ m $ vertices such that its center coincides with the center of the initial polygon and each of its vertices is some vertex of the initial polygon. You have to answer $ t $ independent test cases.输入输出格式
输入格式
The first line of the input contains one integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases. The next $ t $ lines describe test cases. Each test case is given as two space-separated integers $ n $ and $ m $ ( $ 3 \le m < n \le 100 $ ) — the number of vertices in the initial polygon and the number of vertices in the polygon you want to build.
输出格式
For each test case, print the answer — "YES" (without quotes), if it is possible to build another convex regular polygon with $ m $ vertices such that its center coincides with the center of the initial polygon and each of its vertices is some vertex of the initial polygon and "NO" otherwise.
输入输出样例
输入样例 #1
2
6 3
7 3输出样例 #1
YES
NO