Spiderweb Trees

题目描述

Let's call a graph with $ n $ vertices, each of which has it's own point $ A_i = (x_i, y_i) $ with integer coordinates, a planar tree if: - All points $ A_1, A_2, \ldots, A_n $ are different and no three points lie on the same line. - The graph is a tree, i.e. there are exactly $ n-1 $ edges there exists a path between any pair of vertices. - For all pairs of edges $ (s_1, f_1) $ and $ (s_2, f_2) $ , such that $ s_1 \neq s_2, s_1 \neq f_2, $ $ f_1 \neq s_2 $ , and $ f_1 \neq f_2 $ , the segments $ A_{s_1} A_{f_1} $ and $ A_{s_2} A_{f_2} $ don't intersect. Imagine a planar tree with $ n $ vertices. Consider the convex hull of points $ A_1, A_2, \ldots, A_n $ . Let's call this tree a spiderweb tree if for all $ 1 \leq i \leq n $ the following statements are true: - All leaves (vertices with degree $ \leq 1 $ ) of the tree lie on the border of the convex hull. - All vertices on the border of the convex hull are leaves. An example of a spiderweb tree: 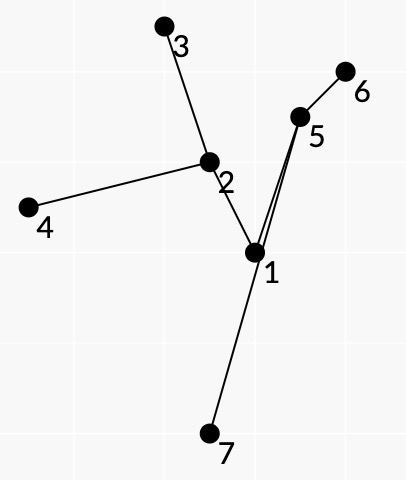The points $ A_3, A_6, A_7, A_4 $ lie on the convex hull and the leaf vertices of the tree are $ 3, 6, 7, 4 $ . Refer to the notes for more examples. Let's call the subset $ S \subset \{1, 2, \ldots, n\} $ of vertices a subtree of the tree if for all pairs of vertices in $ S $ , there exists a path that contains only vertices from $ S $ . Note that any subtree of the planar tree is a planar tree. You are given a planar tree with $ n $ vertexes. Let's call a partition of the set $ \{1, 2, \ldots, n\} $ into non-empty subsets $ A_1, A_2, \ldots, A_k $ (i.e. $ A_i \cap A_j = \emptyset $ for all $ 1 \leq i < j \leq k $ and $ A_1 \cup A_2 \cup \ldots \cup A_k = \{1, 2, \ldots, n\} $ ) good if for all $ 1 \leq i \leq k $ , the subtree $ A_i $ is a spiderweb tree. Two partitions are different if there exists some set that lies in one parition, but not the other. Find the number of good partitions. Since this number can be very large, find it modulo $ 998\,244\,353 $ .

输入输出格式

输入格式

The first line contains an integer $ n $ ( $ 1 \leq n \leq 100 $ ) — the number of vertices in the tree. The next $ n $ lines each contain two integers $ x_i, y_i $ ( $ -10^9 \leq x_i, y_i \leq 10^9 $ ) — the coordinates of $ i $ -th vertex, $ A_i $ . The next $ n-1 $ lines contain two integers $ s, f $ ( $ 1 \leq s, f \leq n $ ) — the edges $ (s, f) $ of the tree. It is guaranteed that all given points are different and that no three of them lie at the same line. Additionally, it is guaranteed that the given edges and coordinates of the points describe a planar tree.

输出格式

Print one integer — the number of good partitions of vertices of the given planar tree, modulo $ 998\,244\,353 $ .

输入输出样例

输入样例 #1

4
0 0
0 1
-1 -1
1 -1
1 2
1 3
1 4

输出样例 #1

5

输入样例 #2

5
3 2
0 -3
-5 -3
5 -5
4 5
4 2
4 1
5 2
2 3

输出样例 #2

8

输入样例 #3

6
4 -5
0 1
-2 8
3 -10
0 -1
-4 -5
2 5
3 2
1 2
4 6
4 2

输出样例 #3

13

输入样例 #4

8
0 0
-1 2
-2 5
-5 1
1 3
0 3
2 4
-1 -4
1 2
3 2
5 6
4 2
1 5
5 7
5 8

输出样例 #4

36

说明

如果下面的条件均为真，那么把一个有 n 个顶点的图形称为蜘蛛网树，每个顶点都有自己的点$ A_i = (x _ i, y _ i)$，并且坐标为整数： - 所有的点 $A_1$, $A_2$ , $A_2$, $A_2$, $A_n$ 都是不同的，而且没有三个点位于同一条线上。 - 该图是一棵树，也就是说，在任何一对顶点之间恰好存在着$ n-1$ 边缘，在任何一对顶点之间存在一条路径。 - 对于所有的一对边 $ (s_1, f_1) $ 和 $ (s_2, f_2) $ ，例如 $ s_1 ≌ s_2, s_1≌ f_2, $ f_1≌ s_2, $ f_1≌ f_2, $ f_1≌ f_2, $ a_{s_1} 的段。A_{f_1} $ 和 $ A_{s_2} A_{f_2} $ 不相交。 想象一个蜘蛛网树，其顶点为$n$个。考虑点 $A_1$ , $A_2$, $A_2$, $A_n$ $ 的凸体。如果以下语句为真，那么称这棵树为蜘蛛网树： - 树的所有叶子（度数为 $1$ 的顶点）都位于凸壳的边界上。 - 凸壳的边界上的所有顶点都是叶子。 下图是蜘蛛网树的一个例子:  点 $A_3$, $A_6$, $A_7$, $A_4$位于顶点上，树的叶子顶点是 $3$, $6$, $7$, 4。 更多的例子请参考下面的注释。 让我们把顶点的子集$S$称为树的子树，如果对于 $S$ 中的所有顶点对，存在一条只包含来自$S$的顶点的路径，则该树的子树为子树。 注意，平面树的任何子树都是平面树。 给出一个有 n 个顶点的蜘蛛网树。让我们把这个集合的分区称为非空子集 $A_1$, $A_2$, $A_2$, $A_dots$, $A_$ (如果在一个分区中存在一些集，而另一个分区中不存在，那么两个分区是不同的。) 找出整数分拆后的的数量。因为这个数字可能很大，所以要找到它的模数 $998 244 353$ 。