Independent Set

题意翻译

### 题目描述 Eric 是一名图论课的老师。这天，Eric 上的是关于点独立集和边导出子图的内容。 给出一张图 $G = (V, E)$，一个点独立集是指点的一个子集 $V' \subset V$，满足对于任意一对 $u, v \in V'$，$(u, v) \not \in E$（也就是说，不存在一条 $E$ 中的边，连接的两端点同在 $V'$ 中）。 一个边导出子图包含了边的一个子集 $E' \subset E$，和原图上所有与 $E'$ 中至少一条边有相邻的点。 设有 $E' \subset E$，定义 $G[E']$ 表示一个以 $E'$ 作为边集的边导出子图。这是对于上述定义的一个图例说明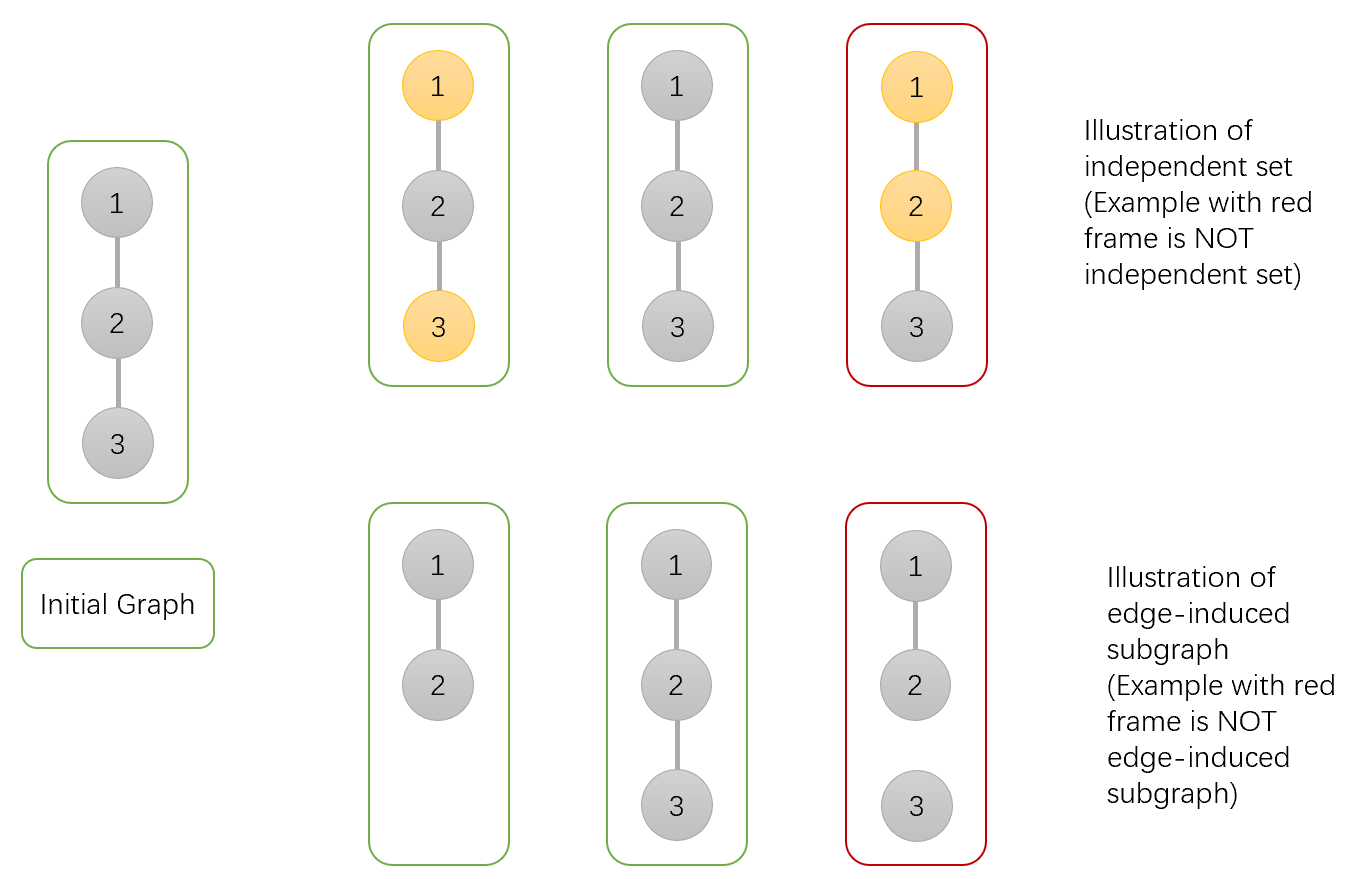：  为了帮助他的学生们熟悉这些定义，Eric 留下了这样一个问题作为练习： 给出一棵树 $G = (V, E)$，对于 $G$ 中所有的非空边导出子图 $H$，计算 $w(H)$ 之和。其中 $w(H)$ 表示 $H$ 中点独立集的种类数。形式化地说，求 $\sum \limits_{\emptyset \not= E' \subset E} w(G[E'])$。 为了向 Eric 展现你比他的学生们都要厉害，请你尽可能快地求出正确答案。注意答案可能很大，你需要输出它对 $998, 244, 353$ 取模的值。 ### 输入格式 第一行输入一个整数 $n ~ (2 \le n \le 3 \cdot 10 ^ 5)$，表示 $G$ 中的点数。 接下来 $n - 1$ 行，每行输入两个整数 $u, v ~ (1 \le u, v \le n; u \neq v)$，表示给定树中的边。 保证输入的边形成一棵树。 ### 输出格式 输出一行一个整数，表示所求答案对 $998, 244, 353$ 取模的值。

题目描述

Eric is the teacher of graph theory class. Today, Eric teaches independent set and edge-induced subgraph. Given a graph $ G=(V,E) $ , an independent set is a subset of vertices $ V' \subset V $ such that for every pair $ u,v \in V' $ , $ (u,v) \not \in E $ (i.e. no edge in $ E $ connects two vertices from $ V' $ ). An edge-induced subgraph consists of a subset of edges $ E' \subset E $ and all the vertices in the original graph that are incident on at least one edge in the subgraph. Given $ E' \subset E $ , denote $ G[E'] $ the edge-induced subgraph such that $ E' $ is the edge set of the subgraph. Here is an illustration of those definitions: In order to help his students get familiar with those definitions, he leaves the following problem as an exercise: Given a tree $ G=(V,E) $ , calculate the sum of $ w(H) $ over all except null edge-induced subgraph $ H $ of $ G $ , where $ w(H) $ is the number of independent sets in $ H $ . Formally, calculate $ \sum \limits_{\emptyset \not= E' \subset E} w(G[E']) $ . Show Eric that you are smarter than his students by providing the correct answer as quickly as possible. Note that the answer might be large, you should output the answer modulo $ 998,244,353 $ .

输入输出格式

输入格式

The first line contains a single integer $ n $ ( $ 2 \le n \le 3 \cdot 10^5 $ ), representing the number of vertices of the graph $ G $ . Each of the following $ n-1 $ lines contains two integers $ u $ and $ v $ ( $ 1 \le u,v \le n $ , $ u \not= v $ ), describing edges of the given tree. It is guaranteed that the given edges form a tree.

输出格式

Output one integer, representing the desired value modulo $ 998,244,353 $ .

输入输出样例

输入样例 #1

2
2 1

输出样例 #1

3

输入样例 #2

3
1 2
3 2

输出样例 #2

11

说明

For the second example, all independent sets are listed below.