Tree Modification

题意翻译

给定一棵$n$个点的树，一次操作，你可以选定三个点$a,b,c$，要求$a$与$b$相邻，$b$与$c$相邻，然后进行如下操作： - 所有与$a$相邻的节点和$c$连边； - 断掉连接$a$与其所有相邻节点的边； - $a$与$c$连边。 你需要最小化操作次数，使得这棵树仅存在一个节点度数为$n-1$，其他节点的度数都为$1$。不需要输出方案。 $n \leq 2 \times 10^5$。

题目描述

You are given a tree with $ n $ vertices. You are allowed to modify the structure of the tree through the following multi-step operation: 1. Choose three vertices $ a $ , $ b $ , and $ c $ such that $ b $ is adjacent to both $ a $ and $ c $ . 2. For every vertex $ d $ other than $ b $ that is adjacent to $ a $ , remove the edge connecting $ d $ and $ a $ and add the edge connecting $ d $ and $ c $ . 3. Delete the edge connecting $ a $ and $ b $ and add the edge connecting $ a $ and $ c $ . As an example, consider the following tree: 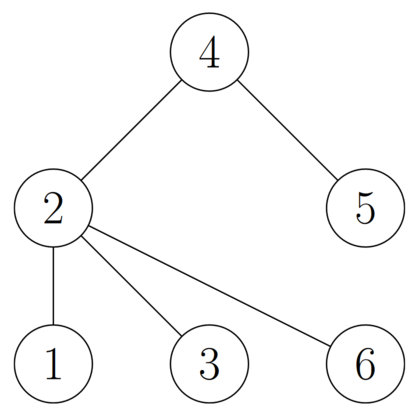The following diagram illustrates the sequence of steps that happen when we apply an operation to vertices $ 2 $ , $ 4 $ , and $ 5 $ : 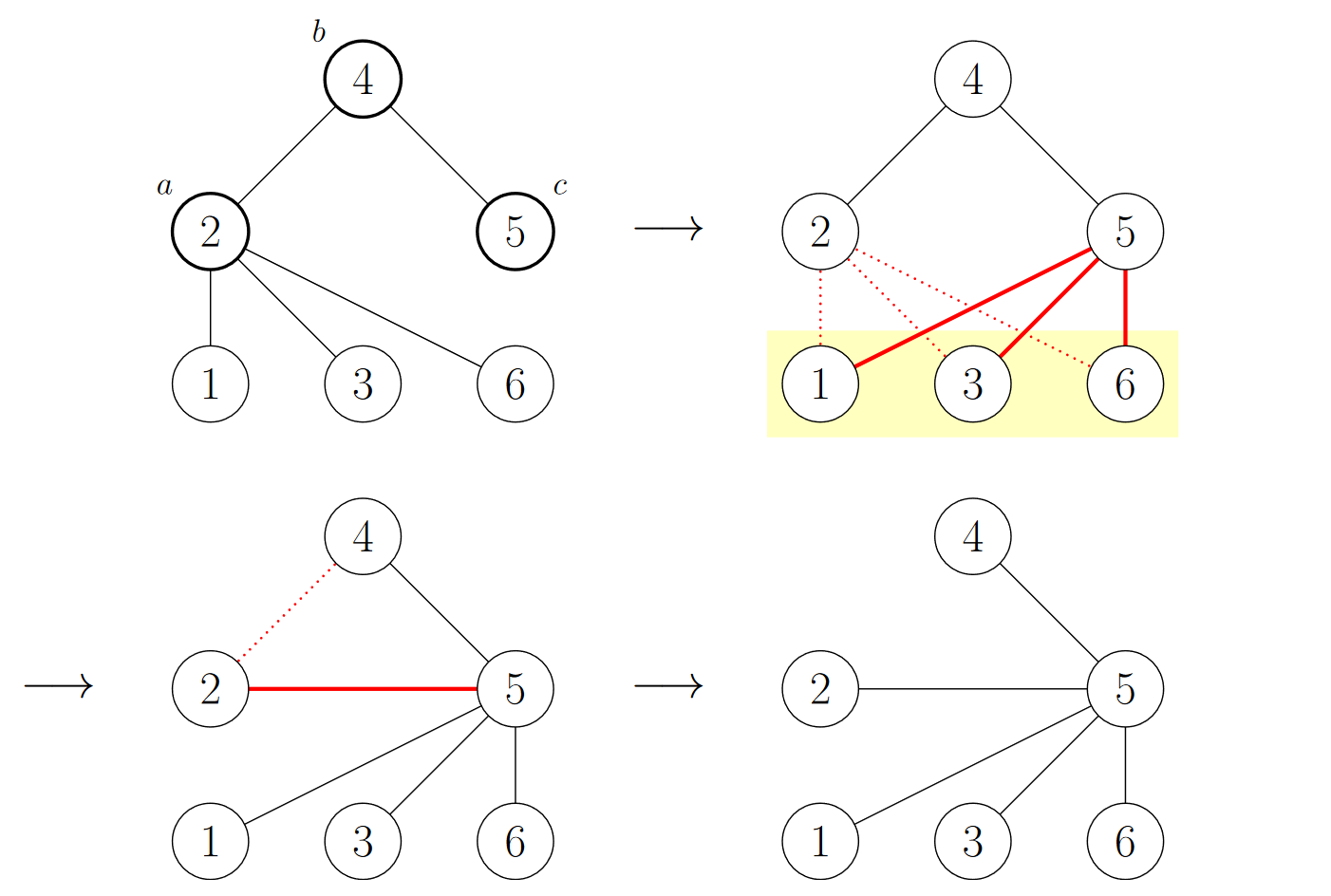It can be proven that after each operation, the resulting graph is still a tree. Find the minimum number of operations that must be performed to transform the tree into a star. A star is a tree with one vertex of degree $ n - 1 $ , called its center, and $ n - 1 $ vertices of degree $ 1 $ .

输入输出格式

输入格式

The first line contains an integer $ n $ ( $ 3 \le n \le 2 \cdot 10^5 $ ) — the number of vertices in the tree. The $ i $ -th of the following $ n - 1 $ lines contains two integers $ u_i $ and $ v_i $ ( $ 1 \le u_i, v_i \le n $ , $ u_i \neq v_i $ ) denoting that there exists an edge connecting vertices $ u_i $ and $ v_i $ . It is guaranteed that the given edges form a tree.

输出格式

Print a single integer — the minimum number of operations needed to transform the tree into a star. It can be proven that under the given constraints, it is always possible to transform the tree into a star using at most $ 10^{18} $ operations.

输入输出样例

输入样例 #1

6
4 5
2 6
3 2
1 2
2 4

输出样例 #1

1

输入样例 #2

4
2 4
4 1
3 4

输出样例 #2

0

说明

The first test case corresponds to the tree shown in the statement. As we have seen before, we can transform the tree into a star with center at vertex $ 5 $ by applying a single operation to vertices $ 2 $ , $ 4 $ , and $ 5 $ . In the second test case, the given tree is already a star with the center at vertex $ 4 $ , so no operations have to be performed.