New Passenger Trams

题意翻译

Kirnes 星球的一天由 $h$ 小时，每小时 $m$ 分钟组成（$m$ 是偶数）。每天有 $n$ 辆货车从 Kirnes 出发，其中第 $i$ 辆的出发时间是 $h_i$ 时 $m_i$ 分。 现计划增添 $2h$ 辆电车，第一辆电车出发于 $0$ 时 $t$ 分，电车的发车间隔为 $\dfrac{m}{2}$ 分钟。形式化地，若 $i$ 为奇数，则第 $i$ 辆电车出发于 $\dfrac{i-1}{2}$ 时 $t+\dfrac{m}{2}$ 分；若 $i$ 为偶数，则第 $i$ 辆电车出发于 $\dfrac{i}{2}$ 时 $t$ 分。$t$ 是一个可以由你决定的整数。 乘客上车需要 $k$ 分钟，为了保证安全，每辆电车出发的前 $k$ 分钟都不能有货车出发。特别地，乘客开始上车的瞬间和电车出发的瞬间，货车可以出发。 为了满足上述要求，必须要取消一些货车。选择合适的 $t$，使得取消的货车数最小。

题目描述

There are many freight trains departing from Kirnes planet every day. One day on that planet consists of $ h $ hours, and each hour consists of $ m $ minutes, where $ m $ is an even number. Currently, there are $ n $ freight trains, and they depart every day at the same time: $ i $ -th train departs at $ h_i $ hours and $ m_i $ minutes. The government decided to add passenger trams as well: they plan to add a regular tram service with half-hour intervals. It means that the first tram of the day must depart at $ 0 $ hours and $ t $ minutes, where $ 0 \le t < {m \over 2} $ , the second tram departs $ m \over 2 $ minutes after the first one and so on. This schedule allows exactly two passenger trams per hour, which is a great improvement. To allow passengers to board the tram safely, the tram must arrive $ k $ minutes before. During the time when passengers are boarding the tram, no freight train can depart from the planet. However, freight trains are allowed to depart at the very moment when the boarding starts, as well as at the moment when the passenger tram departs. Note that, if the first passenger tram departs at $ 0 $ hours and $ t $ minutes, where $ t < k $ , then the freight trains can not depart during the last $ k - t $ minutes of the day. 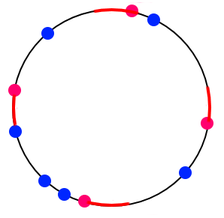A schematic picture of the correct way to run passenger trams. Here $ h=2 $ (therefore, the number of passenger trams is $ 2h=4 $ ), the number of freight trains is $ n=6 $ . The passenger trams are marked in red (note that the spaces between them are the same). The freight trains are marked in blue. Time segments of length $ k $ before each passenger tram are highlighted in red. Note that there are no freight trains inside these segments. Unfortunately, it might not be possible to satisfy the requirements of the government without canceling some of the freight trains. Please help the government find the optimal value of $ t $ to minimize the number of canceled freight trains in case all passenger trams depart according to schedule.

输入输出格式

输入格式

The first line of input contains four integers $ n $ , $ h $ , $ m $ , $ k $ ( $ 1 \le n \le 100\,000 $ , $ 1 \le h \le 10^9 $ , $ 2 \le m \le 10^9 $ , $ m $ is even, $ 1 \le k \le {m \over 2} $ ) — the number of freight trains per day, the number of hours and minutes on the planet, and the boarding time for each passenger tram. $ n $ lines follow, each contains two integers $ h_i $ and $ m_i $ ( $ 0 \le h_i < h $ , $ 0 \le m_i < m $ ) — the time when $ i $ -th freight train departs. It is guaranteed that no freight trains depart at the same time.

输出格式

The first line of output should contain two integers: the minimum number of trains that need to be canceled, and the optimal starting time $ t $ . Second line of output should contain freight trains that need to be canceled.

输入输出样例

输入样例 #1

2 24 60 15
16 0
17 15

输出样例 #1

0 0

输入样例 #2

2 24 60 16
16 0
17 15

输出样例 #2

1 0
2

说明

In the first test case of the example the first tram can depart at 0 hours and 0 minutes. Then the freight train at 16 hours and 0 minutes can depart at the same time as the passenger tram, and the freight train at 17 hours and 15 minutes can depart at the same time as the boarding starts for the upcoming passenger tram. In the second test case of the example it is not possible to design the passenger tram schedule without cancelling any of the freight trains: if $ t \in [1, 15] $ , then the freight train at 16 hours and 0 minutes is not able to depart (since boarding time is 16 minutes). If $ t = 0 $ or $ t \in [16, 29] $ , then the freight train departing at 17 hours 15 minutes is not able to depart. However, if the second freight train is canceled, one can choose $ t = 0 $ . Another possible option is to cancel the first train and choose $ t = 13 $ .