Boboniu Walks on Graph

题意翻译

## 题目描述 Boboniu有一条n个点和m条边的有向图 每个点的出度最大为k 每一条边都有一个权值，没有两条边有相同的权值。 Boboniu喜欢在图上以某种特定的方式走路，这个方式可以表示为特定的集合$(c_1,c_2,\dots,c_k)$。如果他现在在的点的初度为$i$，那么他会走到u的出边中权值第$c_i$小的边 现在bobiniu要你计算所有满足下列条件的边数： - 对于任意的i（$1 \leq i \leq k$），$1 \leq c_i \leq i$ - 对于任意的点u，按上述方式都可以走回自己 ## 输入格式 第一行有三个数n,m,k$(2 \leq n \leq 2*10^5,2 \leq m \leq min(2*10^5,n*(n-1)),1 \leq k \leq 9)$ 接下来有m行，每行三个数u,v,w$(1 \leq u,v \leq n,u \neq v,1 \leq w \leq m)$，表示一条从u到v的边。保证没有自环和重边。保证所有点都至少有1条出边 保证所有点出度最多为k，保证没有两条边权值相同 ## 输出格式 一个数：环的个数 ## 说明 样例1有两种方案：(1,1,3)和(1,2,3)，图中蓝的边是boboniu决定走的边 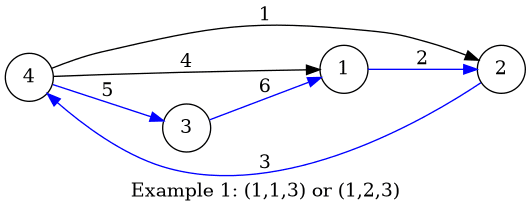 样例3只有一种方案：(1,2,2,2) 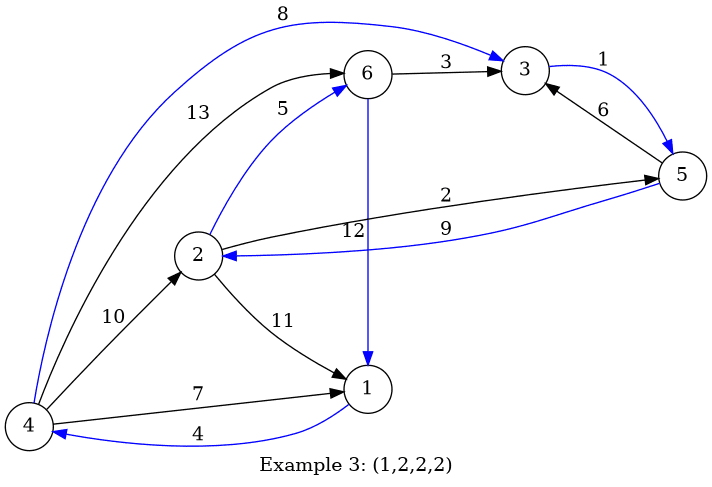 点的出度表示从这个点出去的边的条数

题目描述

Boboniu has a directed graph with $ n $ vertices and $ m $ edges. The out-degree of each vertex is at most $ k $ . Each edge has an integer weight between $ 1 $ and $ m $ . No two edges have equal weights. Boboniu likes to walk on the graph with some specific rules, which is represented by a tuple $ (c_1,c_2,\ldots,c_k) $ . If he now stands on a vertex $ u $ with out-degree $ i $ , then he will go to the next vertex by the edge with the $ c_i $ -th $ (1\le c_i\le i) $ smallest weight among all edges outgoing from $ u $ . Now Boboniu asks you to calculate the number of tuples $ (c_1,c_2,\ldots,c_k) $ such that - $ 1\le c_i\le i $ for all $ i $ ( $ 1\le i\le k $ ). - Starting from any vertex $ u $ , it is possible to go back to $ u $ in finite time by walking on the graph under the described rules.

输入输出格式

输入格式

The first line contains three integers $ n $ , $ m $ and $ k $ ( $ 2\le n\le 2\cdot 10^5 $ , $ 2\le m\le \min(2\cdot 10^5,n(n-1) ) $ , $ 1\le k\le 9 $ ). Each of the next $ m $ lines contains three integers $ u $ , $ v $ and $ w $ $ (1\le u,v\le n,u\ne v,1\le w\le m) $ , denoting an edge from $ u $ to $ v $ with weight $ w $ . It is guaranteed that there are no self-loops or multiple edges and each vertex has at least one edge starting from itself. It is guaranteed that the out-degree of each vertex is at most $ k $ and no two edges have equal weight.

输出格式

Print one integer: the number of tuples.

输入输出样例

输入样例 #1

4 6 3
4 2 1
1 2 2
2 4 3
4 1 4
4 3 5
3 1 6

输出样例 #1

2

输入样例 #2

5 5 1
1 4 1
5 1 2
2 5 3
4 3 4
3 2 5

输出样例 #2

1

输入样例 #3

6 13 4
3 5 1
2 5 2
6 3 3
1 4 4
2 6 5
5 3 6
4 1 7
4 3 8
5 2 9
4 2 10
2 1 11
6 1 12
4 6 13

输出样例 #3

1

说明

For the first example, there are two tuples: $ (1,1,3) $ and $ (1,2,3) $ . The blue edges in the picture denote the $ c_i $ -th smallest edges for each vertex, which Boboniu chooses to go through. For the third example, there's only one tuple: $ (1,2,2,2) $ . The out-degree of vertex $ u $ means the number of edges outgoing from $ u $ .

题意翻译

## 题目描述 Boboniu有一条n个点和m条边的有向图 每个点的出度最大为k 每一条边都有一个权值，没有两条边有相同的权值。 Boboniu喜欢在图上以某种特定的方式走路，这个方式可以表示为特定的集合$(c_1,c_2,\dots,c_k)$。如果他现在在的点的初度为$i$，那么他会走到u的出边中权值第$c_i$小的边 现在bobiniu要你计算所有满足下列条件的边数： - 对于任意的i（$1 \leq i \leq k$），$1 \leq c_i \leq i$ - 对于任意的点u，按上述方式都可以走回自己 ## 输入格式 第一行有三个数n,m,k$(2 \leq n \leq 2*10^5,2 \leq m \leq min(2*10^5,n*(n-1)),1 \leq k \leq 9)$ 接下来有m行，每行三个数u,v,w$(1 \leq u,v \leq n,u \neq v,1 \leq w \leq m)$，表示一条从u到v的边。保证没有自环和重边。保证所有点都至少有1条出边 保证所有点出度最多为k，保证没有两条边权值相同 ## 输出格式 一个数：环的个数 ## 说明 样例1有两种方案：(1,1,3)和(1,2,3)，图中蓝的边是boboniu决定走的边  样例3只有一种方案：(1,2,2,2)  点的出度表示从这个点出去的边的条数