Prison Break

题意翻译

### 题面描述 一个囚犯想从监狱里逃出来。监狱由顶点P1,P2,P3,...,Pn+1,Pn+2,Pn+3的凸多边形表示。 监狱的墙壁Pn+1Pn+2,Pn+2Pn+3和Pn+3P1非常高，犯人爬不上去。因此，他唯一的机会是到达其中一个墙上的点P1 P2,P2 P3，…，Pn Pn+1，然后逃离那里。在监狱的四周，有两名警卫。囚犯以1的速度移动，而狱警则始终保持在监狱的外围，速度是v。 如果犯人到达了有守卫的边界，守卫杀死了犯人。如果犯人到达了边界的某个点，他可以爬上去，而且那里没有警卫，他会立即逃跑。最初，囚犯在点 (-10^17,h/2)，警卫在点P1。 找到最小速度v，这样警卫可以保证囚犯不会逃跑(假设囚犯和警卫都以最佳方式移动)。 注: - 看守和囚犯随时都能看到对方。 - “逃生”的“攀登部分”不计时间。 - 你可以假设囚犯和看守都能立即改变方向和速度，而且他们都有完美的反应能力(所以他们可以对另一个人的行为做出即时反应)。 - 这两个警卫可以提前计划如何应对囚犯的行动。 ### 输入格式 输入的第一行包含 n (1≤n≤50) 下面的n + 1行描述P1,P2,…,Pn + 1。这些行的每行包含两个整数xi,yi (0≤xi,yi≤1000)--Pi的坐标 =(xi,yi) 它保证P1 =(0, 0)和xn + 1 = 0。由顶点P1,P2,…,Pn+1,Pn+2,Pn+3组成的多边形(其中Pn+2、Pn+3必须按照语句描述构造)保证为凸多边形，且不存在包含其三个顶点的直线。 ### 输出格式 输出一个数字，最小的速度v，让看守保证囚犯不会逃跑。如果你的答案的相对或绝对误差不超过10^-6，你的答案将被认为是正确的。

题目描述

A prisoner wants to escape from a prison. The prison is represented by the interior of the convex polygon with vertices $ P_1, P_2, P_3, \ldots, P_{n+1}, P_{n+2}, P_{n+3} $ . It holds $ P_1=(0,0) $ , $ P_{n+1}=(0, h) $ , $ P_{n+2}=(-10^{18}, h) $ and $ P_{n+3}=(-10^{18}, 0) $ . 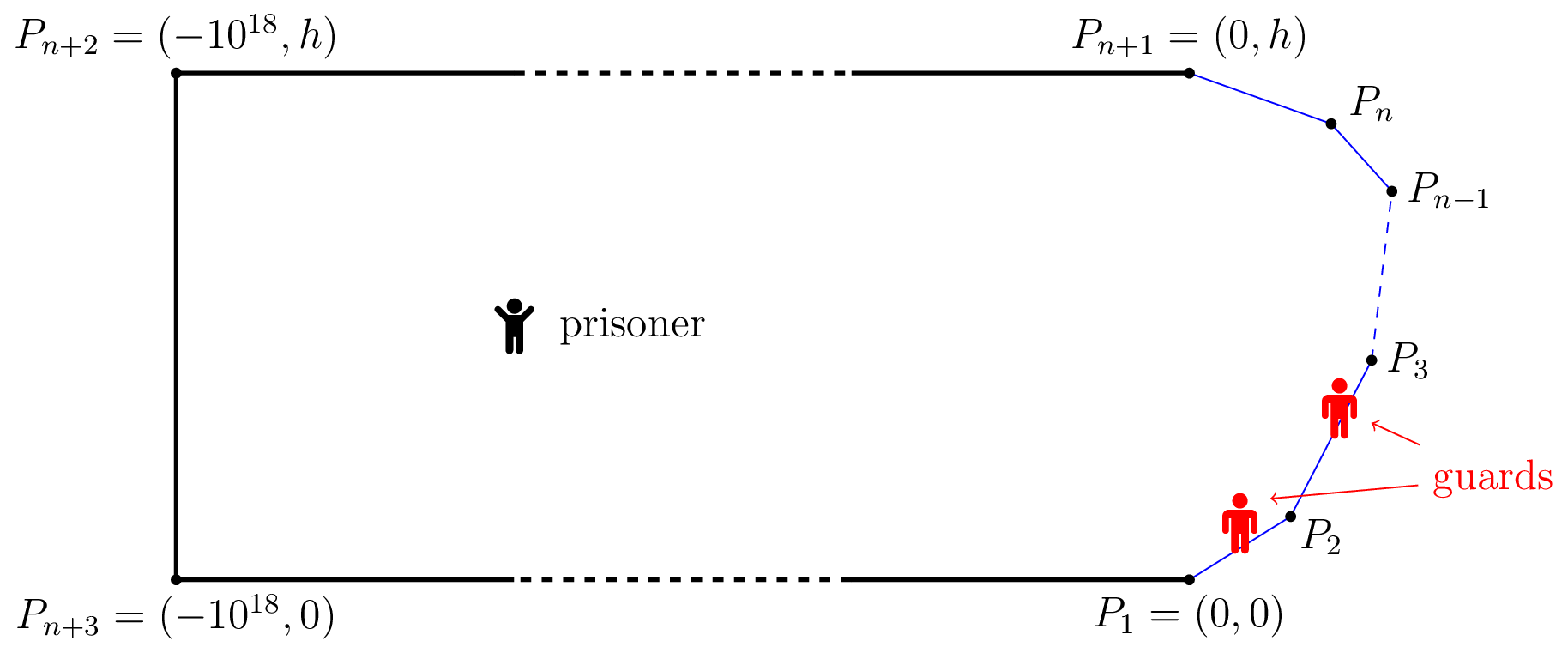The prison walls $ P_{n+1}P_{n+2} $ , $ P_{n+2}P_{n+3} $ and $ P_{n+3}P_1 $ are very high and the prisoner is not able to climb them. Hence his only chance is to reach a point on one of the walls $ P_1P_2, P_2P_3,\dots, P_{n}P_{n+1} $ and escape from there. On the perimeter of the prison, there are two guards. The prisoner moves at speed $ 1 $ while the guards move, remaining always on the perimeter of the prison, with speed $ v $ . If the prisoner reaches a point of the perimeter where there is a guard, the guard kills the prisoner. If the prisoner reaches a point of the part of the perimeter he is able to climb and there is no guard there, he escapes immediately. Initially the prisoner is at the point $ (-10^{17}, h/2) $ and the guards are at $ P_1 $ . Find the minimum speed $ v $ such that the guards can guarantee that the prisoner will not escape (assuming that both the prisoner and the guards move optimally). Notes: - At any moment, the guards and the prisoner can see each other. - The "climbing part" of the escape takes no time. - You may assume that both the prisoner and the guards can change direction and velocity instantly and that they both have perfect reflexes (so they can react instantly to whatever the other one is doing). - The two guards can plan ahead how to react to the prisoner movements.

输入输出格式

输入格式

The first line of the input contains $ n $ ( $ 1 \le n \le 50 $ ). The following $ n+1 $ lines describe $ P_1, P_2,\dots, P_{n+1} $ . The $ i $ -th of such lines contain two integers $ x_i $ , $ y_i $ ( $ 0\le x_i, y_i\le 1,000 $ ) — the coordinates of $ P_i=(x_i, y_i) $ . It is guaranteed that $ P_1=(0,0) $ and $ x_{n+1}=0 $ . The polygon with vertices $ P_1,P_2,\dots, P_{n+1}, P_{n+2}, P_{n+3} $ (where $ P_{n+2}, P_{n+3} $ shall be constructed as described in the statement) is guaranteed to be convex and such that there is no line containing three of its vertices.

输出格式

Print a single real number, the minimum speed $ v $ that allows the guards to guarantee that the prisoner will not escape. Your answer will be considered correct if its relative or absolute error does not exceed $ 10^{-6} $ .

输入输出样例

输入样例 #1

2
0 0
223 464
0 749

输出样例 #1

1

输入样例 #2

3
0 0
2 2
2 4
0 6

输出样例 #2

1.0823922

输入样例 #3

4
0 0
7 3
7 4
5 7
0 8

输出样例 #3

1.130309669

输入样例 #4

5
0 0
562 248
460 610
281 702
206 723
0 746

输出样例 #4

1.148649561

输入样例 #5

7
0 0
412 36
745 180
747 184
746 268
611 359
213 441
0 450

输出样例 #5

1.134745994