Multithreading (Easy Version)

题意翻译

有一个长度为 $n$ 的偶数，每个点可以是黑色也可以是白色。黑色点和白色点的数量都是偶数。 同色的点可以连边，边的颜色与这对点的颜色相同，你需要找到一组匹配，使得异色且相交的边数尽可能少。 你有一个字符串来描述此环，长度为 $n$，其中 ```b,w``` 分别表示白色和黑色，其中的 ```?``` 代表问号，你需要求出在 ```?``` 任意为 ```b,w``` 时（需要满足数量分别为偶数）情况下，异色且相交的边数的最小值的期望。 支持修改。 $n,m\le 2\times 10^5$，对于简单版本，保证 $m=0$

题目描述

The only difference between the two versions of the problem is that there are no updates in the easy version. There are $ n $ spools of thread placed on the rim of a circular table. The spools come in two types of thread: the first thread is black and the second thread is white. For any two spools of the same color, you can attach them with a thread of that color in a straight line segment. Define a matching as a way to attach spools together so that each spool is attached to exactly one other spool. Coloring is an assignment of colors (white and black) to the spools. A coloring is called valid if it has at least one matching. That is if the number of black spools and the number of white spools are both even. Given a matching, we can find the number of times some white thread intersects some black thread. We compute the number of pairs of differently colored threads that intersect instead of the number of intersection points, so one intersection point may be counted multiple times if different pairs of threads intersect at the same point. If $ c $ is a valid coloring, let $ f(c) $ denote the minimum number of such intersections out of all possible matchings. 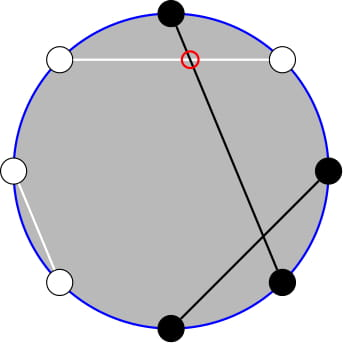 The circle above is described by the coloring bwbbbwww. After matching the spools as shown, there is one intersection between differently colored threads. It can be proven that it is the minimum possible, so $ f(\text{bwbbbwww}) = 1 $ . You are given a string $ s $ representing an unfinished coloring, with black, white, and uncolored spools. A coloring $ c $ is called $ s $ -reachable if you can achieve it by assigning colors to the uncolored spools of $ s $ without changing the others. A coloring $ c $ is chosen uniformly at random among all valid, $ s $ -reachable colorings. Compute the [expected value](https://en.wikipedia.org/wiki/Expected_value) of $ f(c) $ . You should find it by modulo $ 998244353 $ . We can show that the answer can be written in the form $ \frac{p}{q} $ where $ p $ and $ q $ are relatively prime integers and $ q\not\equiv 0\pmod{998244353} $ . The answer by modulo $ 998244353 $ is equal to $ (p\cdot q^{-1}) $ modulo $ 998244353 $ .

输入输出格式

输入格式

The first line contains two integers $ n $ , $ m $ ( $ 2\le n\le 2\cdot 10^5 $ , $ n $ is even, $ m=0 $ ) — the number of spools and updates, respectively. There are no updates in the easy version, so it is always $ 0 $ . The second line contains a string $ s $ of length $ n $ — the unfinished coloring of the spools. The $ i $ -th character will be 'w', 'b', or '?', describing if the $ i $ -th spool is white, black, or uncolored, respectively. It is guaranteed there exists at least one uncolored spool.

输出格式

Print the expected value of $ f(c) $ by modulo $ 998244353 $ .

输入输出样例

输入样例 #1

8 0
bwbb?www

输出样例 #1

1

输入样例 #2

10 0
???ww?wb??

输出样例 #2

436731905

输入样例 #3

4 0
bw?b

输出样例 #3

0

说明

The first test corresponds closely to the image. Coloring '?' as 'w' does not create a valid coloring because the number of black spools is odd. Then the only reachable valid coloring is 'bwbbbwww' and $ f(\text{bwbbbwww}) = 1 $ , so the expected value is $ 1 $ . It can be shown that the expected value for the second test is $ \frac{9}{16} $ .

题意翻译

有一个长度为 $n$ 的偶数，每个点可以是黑色也可以是白色。黑色点和白色点的数量都是偶数。 同色的点可以连边，边的颜色与这对点的颜色相同，你需要找到一组匹配，使得异色且相交的边数尽可能少。 你有一个字符串来描述此环，长度为 $n$，其中 ```b,w``` 分别表示白色和黑色，其中的 ```?``` 代表问号，你需要求出在 ```?``` 任意为 ```b,w``` 时（需要满足数量分别为偶数）情况下，异色且相交的边数的最小值的期望。 支持修改。 $n,m\le 2\times 10^5$，对于简单版本，保证 $m=0$