Cancel the Trains

题意翻译

`Gildong` 有一列车系统。从左到右，从下到上分别有 $100$ 头列车。从每侧出发的列车从 $1$ 到 $100$ 编号，所有列车的速度相同。如图。 列车系统可以用二维平面上的坐标表示。每一头列车视为一个点，从底部开始的第 $i$ 头列车最初在 $(i,0)$ ，并将在 $T$ 分钟后到达 $(i,T)$，从左端开始的第 $i$ 列车最初在 $(0,i)$ ，在 $T$ 分钟后将在 $(T,i)$ 开始。所有列车在 $101$ 分钟后到达目的地。 然而，`Gildong` 发现，一些在特定时间发车的列车，是存在危险的。这时，有 $n$ 头列车计划从底端发车，$m$ 列车计划从左端发车。如果两列火车同时处于 $(x,y)$ 的位置，那么它们会相撞。因此，`Gildong` 要求你找出应该取消的最小列车数，以防止所有碰撞发生。 #### 输入格式 每个数据点**包含一个或多组数据**。第一行包含测试组数 $t (1\le t\le 100)$。 每个测试数据包含三行。 第一行两个整数 $n$ 和$m (1\le n,m\le 100)$，代表计划从底端出发的列车数和计划从左端出发的列车数。 第二行包含 $n$ 个整数。每个整数代表从底端开始的列车号。这些数字是按严格递增的顺序给出的，介于 $1$ 到 $100$ 之间（含 $1$ 和 $100$）。 第三行包含 $m$ 个整数。每个整数代表从左端开始的列车号。这些数字是按严格递增的顺序给出的，介于 $1$ 到 $100$ 之间（含 $1$ 和 $100$）。 #### 输出格式 对于每个测试用例，输出一个整数：为了防止所有碰撞，应该取消的最小列车数。 #### 说明/提示 对于第一组数据，可以证明，无论什么时候，都不会发生碰撞。因此，答案是 $0$。 对于第二组数据，当 $T=4$时，会发生碰撞，如图所示。可以证明，取消其中一头列车后，剩下的火车不会相撞。因此，答案是 $1$。

题目描述

Gildong's town has a train system that has $ 100 $ trains that travel from the bottom end to the top end and $ 100 $ trains that travel from the left end to the right end. The trains starting from each side are numbered from $ 1 $ to $ 100 $ , respectively, and all trains have the same speed. Let's take a look at the picture below. 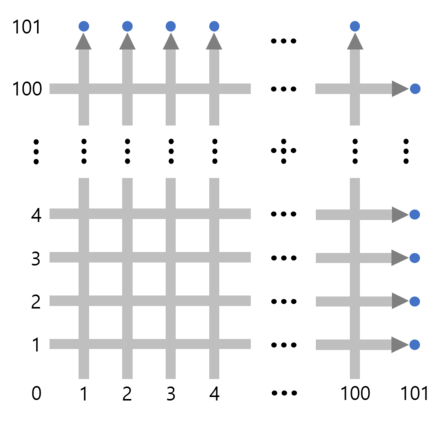The train system can be represented as coordinates on a 2D plane. The $ i $ -th train starting at the bottom end is initially at $ (i,0) $ and will be at $ (i,T) $ after $ T $ minutes, and the $ i $ -th train starting at the left end is initially at $ (0,i) $ and will be at $ (T,i) $ after $ T $ minutes. All trains arrive at their destinations after $ 101 $ minutes. However, Gildong found that some trains scheduled to depart at a specific time, simultaneously, are very dangerous. At this time, $ n $ trains are scheduled to depart from the bottom end and $ m $ trains are scheduled to depart from the left end. If two trains are both at $ (x,y) $ at the same time for some $ x $ and $ y $ , they will crash into each other. Therefore, he is asking you to find the minimum number of trains that should be cancelled to prevent all such crashes.

输入输出格式

输入格式

Each test contains one or more test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 100 $ ). Each test case contains three lines. The first line of each test case consists of two integers $ n $ and $ m $ ( $ 1 \le n, m \le 100 $ ) — the number of trains scheduled to depart from the bottom end, and the number of trains scheduled to depart from the left end, respectively. The second line of each test case contains $ n $ integers. Each integer is a train number that is scheduled to start from the bottom end. The numbers are given in strictly increasing order, and are between $ 1 $ and $ 100 $ , inclusive. The third line of each test case contains $ m $ integers. Each integer is a train number that is scheduled to start from the left end. The numbers are given in strictly increasing order, and are between $ 1 $ and $ 100 $ , inclusive.

输出格式

For each test case, print a single integer: the minimum number of trains that should be canceled in order to prevent all crashes.

输入输出样例

输入样例 #1

3
1 2
1
3 4
3 2
1 3 4
2 4
9 14
2 7 16 28 33 57 59 86 99
3 9 14 19 25 26 28 35 41 59 85 87 99 100

输出样例 #1

0
1
3

说明

In the first case, we can show that there will be no crashes if the current schedule is followed. Therefore, the answer is zero. In the second case, at $ T=4 $ , there will be a crash, as can be seen in the picture below. We can prove that after canceling one of these trains, the remaining trains will not crash. Therefore, the answer is one.