Tiles

题意翻译

现在有一条由许多瓷砖拼成的路，类似下图所示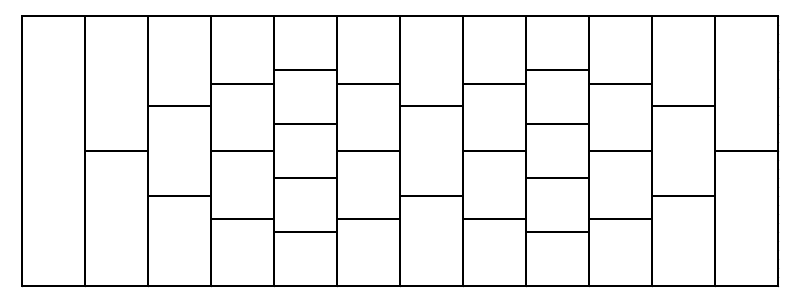：  它的构成方式如下： * 每一列的所有瓷砖都**全等**，第一列仅有 $1$ 块瓷砖。 * 接下来 $a_1$ 列，每列的瓷砖数量都比上一列多 $1$。 * 接下来 $b_1$ 列，每列的瓷砖数量都比上一列少 $1$。 * 接下来 $a_2$ 列，每列的瓷砖数量都比上一列多 $1$。 * 接下来 $b_2$ 列，每列的瓷砖数量都比上一列少 $1$。 * ... * 接下来 $a_n$ 列，每列的瓷砖数量都比上一列多 $1$。 * 接下来 $b_n$ 列，每列的瓷砖数量都比上一列少 $1$。 现在你在第一块瓷砖上，你想要走到最后一列（任意一块瓷砖）上， 且每次只能走到下一列与当前瓷砖接触的任意一块瓷砖。 请你求出方案数，对 $998244353$ 取模。 $n\le1000,1\le a_i,b_i\le10^5,|a_i-b_i|\le 5$。

题目描述

Consider a road consisting of several rows. Each row is divided into several rectangular tiles, and all tiles in the same row are equal. The first row contains exactly one rectangular tile. Look at the picture below which shows how the tiles are arranged. The road is constructed as follows: - the first row consists of $ 1 $ tile; - then $ a_1 $ rows follow; each of these rows contains $ 1 $ tile greater than the previous row; - then $ b_1 $ rows follow; each of these rows contains $ 1 $ tile less than the previous row; - then $ a_2 $ rows follow; each of these rows contains $ 1 $ tile greater than the previous row; - then $ b_2 $ rows follow; each of these rows contains $ 1 $ tile less than the previous row; - ... - then $ a_n $ rows follow; each of these rows contains $ 1 $ tile greater than the previous row; - then $ b_n $ rows follow; each of these rows contains $ 1 $ tile less than the previous row.  An example of the road with $ n = 2 $ , $ a_1 = 4 $ , $ b_1 = 2 $ , $ a_2 = 2 $ , $ b_2 = 3 $ . Rows are arranged from left to right. You start from the only tile in the first row and want to reach the last row (any tile of it). From your current tile, you can move to any tile in the next row which touches your current tile. Calculate the number of different paths from the first row to the last row. Since it can be large, print it modulo $ 998244353 $ .

输入输出格式

输入格式

The first line contains one integer $ n $ ( $ 1 \le n \le 1000 $ ). Then $ n $ lines follow. The $ i $ -th of them contains two integers $ a_i $ and $ b_i $ ( $ 1 \le a_i, b_i \le 10^5 $ ; $ |a_i - b_i| \le 5 $ ). Additional constraint on the input: the sequence of $ a_i $ and $ b_i $ never results in a row with non-positive number of tiles.

输出格式

Print one integer — the number of paths from the first row to the last row, taken modulo $ 998244353 $ .

输入输出样例

输入样例 #1

2
4 2
2 3

输出样例 #1

850

输入样例 #2

3
4 1
2 3
3 1

输出样例 #2

10150

输入样例 #3

8
328 323
867 868
715 718
721 722
439 435
868 870
834 834
797 796

输出样例 #3

759099319

题意翻译

现在有一条由许多瓷砖拼成的路，类似下图所示：  它的构成方式如下： * 每一列的所有瓷砖都**全等**，第一列仅有 $1$ 块瓷砖。 * 接下来 $a_1$ 列，每列的瓷砖数量都比上一列多 $1$。 * 接下来 $b_1$ 列，每列的瓷砖数量都比上一列少 $1$。 * 接下来 $a_2$ 列，每列的瓷砖数量都比上一列多 $1$。 * 接下来 $b_2$ 列，每列的瓷砖数量都比上一列少 $1$。 * ... * 接下来 $a_n$ 列，每列的瓷砖数量都比上一列多 $1$。 * 接下来 $b_n$ 列，每列的瓷砖数量都比上一列少 $1$。 现在你在第一块瓷砖上，你想要走到最后一列（任意一块瓷砖）上， 且每次只能走到下一列与当前瓷砖接触的任意一块瓷砖。 请你求出方案数，对 $998244353$ 取模。 $n\le1000,1\le a_i,b_i\le10^5,|a_i-b_i|\le 5$。