Triangular Paths

题意翻译

### 题目描述 考虑一个多层的“无穷三角形”，每层自上向下从一开始编号。第 $k$ 层有 $k$ 个节点，自左向右从一开始编号。三角形上每个点由坐标 $(r,c)$ 表示，其中前一个坐标表示层，后一个坐标表示序号。对于每个节点 $(r,c)$ 连两条**有向**边到点 $(r+1,c)$ 和 $(r+1,c+1)$，但是只有其中一条边被激活。如果 $r+c$ 是偶数，则到 $(r+1,c)$ 的边被激活。否则到 $(r+1,c+1)$ 的边被激活。如果您不能理解可以看题图理解。图中“被激活的边”为黑色，其他边为灰色。如果可以沿着被激活的边自 $(r_1,c_1)$ 到 $(r_2,c_2)$，称这两个点连通。例如，$(1,1)$ 和 $(3,2)$ 连通，但 $(2,1)$ 和 $(1,1)$ 不连通。 一开始，你在 $1,1$。每一步可以： - 改变激活性。例如，您可以将本来到 $(r+1,c)$ 的激活边去激活并使得到 $(r+1,c+1)$ 的边被激活。这个操作花费 $1$ 的代价。 - 顺着激活的边到达下一层，无需消耗代价。 现在你被给出一个“无穷三角形”上的点的序列 $Q={r_i,c_i}$，现在请你找到花费最小的方式，使得你顺利经过这些点，不必考虑顺序。 ### 输入格式 第一行一个整数 $T$ 表示测试数据组数。 每个数据组以一个整数 $n$ 开头表示序列 $Q$ 中点的个数。（也就是你要经过的点的总数） 第二行包括 $n$ 个整数，第 $i$ 个表示 $r_i$。 第三行包括 $n$ 个整数，第 $i$ 个表示 $c_i$。 数据保证 $n$ 个点互不相同，并一定有解。 ### 输出格式 对于每个测试数据组一个整数，表示最小的花费。 ### 数据范围 $1\leqslant\sum n\leqslant2\times10^5,1\leqslant c_i\leqslant r_i \leqslant 10^9,1\leqslant t\leqslant10^4$

题目描述

Consider an infinite triangle made up of layers. Let's number the layers, starting from one, from the top of the triangle (from top to bottom). The $ k $ -th layer of the triangle contains $ k $ points, numbered from left to right. Each point of an infinite triangle is described by a pair of numbers $ (r, c) $ ( $ 1 \le c \le r $ ), where $ r $ is the number of the layer, and $ c $ is the number of the point in the layer. From each point $ (r, c) $ there are two directed edges to the points $ (r+1, c) $ and $ (r+1, c+1) $ , but only one of the edges is activated. If $ r + c $ is even, then the edge to the point $ (r+1, c) $ is activated, otherwise the edge to the point $ (r+1, c+1) $ is activated. Look at the picture for a better understanding. 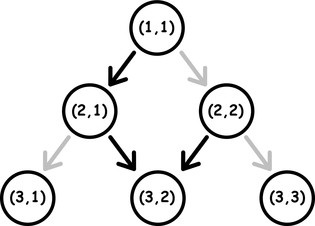Activated edges are colored in black. Non-activated edges are colored in gray.From the point $ (r_1, c_1) $ it is possible to reach the point $ (r_2, c_2) $ , if there is a path between them only from activated edges. For example, in the picture above, there is a path from $ (1, 1) $ to $ (3, 2) $ , but there is no path from $ (2, 1) $ to $ (1, 1) $ . Initially, you are at the point $ (1, 1) $ . For each turn, you can: - Replace activated edge for point $ (r, c) $ . That is if the edge to the point $ (r+1, c) $ is activated, then instead of it, the edge to the point $ (r+1, c+1) $ becomes activated, otherwise if the edge to the point $ (r+1, c+1) $ , then instead if it, the edge to the point $ (r+1, c) $ becomes activated. This action increases the cost of the path by $ 1 $ ; - Move from the current point to another by following the activated edge. This action does not increase the cost of the path. You are given a sequence of $ n $ points of an infinite triangle $ (r_1, c_1), (r_2, c_2), \ldots, (r_n, c_n) $ . Find the minimum cost path from $ (1, 1) $ , passing through all $ n $ points in arbitrary order.

输入输出格式

输入格式

The first line contains one integer $ t $ ( $ 1 \le t \le 10^4 $ ) is the number of test cases. Then $ t $ test cases follow. Each test case begins with a line containing one integer $ n $ ( $ 1 \le n \le 2 \cdot 10^5 $ ) is the number of points to visit. The second line contains $ n $ numbers $ r_1, r_2, \ldots, r_n $ ( $ 1 \le r_i \le 10^9 $ ), where $ r_i $ is the number of the layer in which $ i $ -th point is located. The third line contains $ n $ numbers $ c_1, c_2, \ldots, c_n $ ( $ 1 \le c_i \le r_i $ ), where $ c_i $ is the number of the $ i $ -th point in the $ r_i $ layer. It is guaranteed that all $ n $ points are distinct. It is guaranteed that there is always at least one way to traverse all $ n $ points. It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 2 \cdot 10^5 $ .

输出格式

For each test case, output the minimum cost of a path passing through all points in the corresponding test case.

输入输出样例

输入样例 #1

4
3
1 4 2
1 3 1
2
2 4
2 3
2
1 1000000000
1 1000000000
4
3 10 5 8
2 5 2 4

输出样例 #1

0
1
999999999
2

题意翻译

### 题目描述 考虑一个多层的“无穷三角形”，每层自上向下从一开始编号。第 $k$ 层有 $k$ 个节点，自左向右从一开始编号。三角形上每个点由坐标 $(r,c)$ 表示，其中前一个坐标表示层，后一个坐标表示序号。对于每个节点 $(r,c)$ 连两条**有向**边到点 $(r+1,c)$ 和 $(r+1,c+1)$，但是只有其中一条边被激活。如果 $r+c$ 是偶数，则到 $(r+1,c)$ 的边被激活。否则到 $(r+1,c+1)$ 的边被激活。如果您不能理解可以看题图理解。图中“被激活的边”为黑色，其他边为灰色。如果可以沿着被激活的边自 $(r_1,c_1)$ 到 $(r_2,c_2)$，称这两个点连通。例如，$(1,1)$ 和 $(3,2)$ 连通，但 $(2,1)$ 和 $(1,1)$ 不连通。 一开始，你在 $1,1$。每一步可以： - 改变激活性。例如，您可以将本来到 $(r+1,c)$ 的激活边去激活并使得到 $(r+1,c+1)$ 的边被激活。这个操作花费 $1$ 的代价。 - 顺着激活的边到达下一层，无需消耗代价。 现在你被给出一个“无穷三角形”上的点的序列 $Q={r_i,c_i}$，现在请你找到花费最小的方式，使得你顺利经过这些点，不必考虑顺序。 ### 输入格式 第一行一个整数 $T$ 表示测试数据组数。 每个数据组以一个整数 $n$ 开头表示序列 $Q$ 中点的个数。（也就是你要经过的点的总数） 第二行包括 $n$ 个整数，第 $i$ 个表示 $r_i$。 第三行包括 $n$ 个整数，第 $i$ 个表示 $c_i$。 数据保证 $n$ 个点互不相同，并一定有解。 ### 输出格式 对于每个测试数据组一个整数，表示最小的花费。 ### 数据范围 $1\leqslant\sum n\leqslant2\times10^5,1\leqslant c_i\leqslant r_i \leqslant 10^9,1\leqslant t\leqslant10^4$