How Many Paths?

题意翻译

有一个有向图，图中含有 $n$ 个点 $m$ 条边（边中可能有自环，但是没有重边）。 设顶点 $i$ 的答案为 $ans_i$，则： - 如果不存在一条 $1$ 到 $i$ 的路径，$ans_i$ 为 $0$； - 如果只存在一条 $1$ 到 $i$ 的路径，$ans_i$ 为 $1$； - 如果至少存在两条 $1$ 到 $i$ 的路径，并且路径数量是有限的，$ans_i$ 为 $2$； - 如果存在无限条 $1$ 到 $i$ 的路径，$ans_i$ 为 $-1$。 注意路径不必是简单路径。 对于每一个 $1 \leq i \leq n$，输出 $ans_i$。

题目描述

You are given a directed graph $ G $ which can contain loops (edges from a vertex to itself). Multi-edges are absent in $ G $ which means that for all ordered pairs $ (u, v) $ exists at most one edge from $ u $ to $ v $ . Vertices are numbered from $ 1 $ to $ n $ . A path from $ u $ to $ v $ is a sequence of edges such that: - vertex $ u $ is the start of the first edge in the path; - vertex $ v $ is the end of the last edge in the path; - for all pairs of adjacent edges next edge starts at the vertex that the previous edge ends on. We will assume that the empty sequence of edges is a path from $ u $ to $ u $ . For each vertex $ v $ output one of four values: - $ 0 $ , if there are no paths from $ 1 $ to $ v $ ; - $ 1 $ , if there is only one path from $ 1 $ to $ v $ ; - $ 2 $ , if there is more than one path from $ 1 $ to $ v $ and the number of paths is finite; - $ -1 $ , if the number of paths from $ 1 $ to $ v $ is infinite. Let's look at the example shown in the figure. 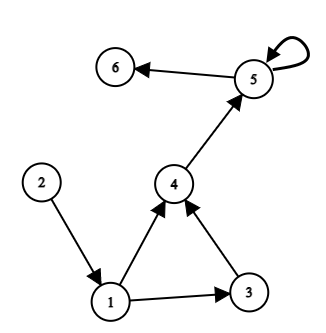Then: - the answer for vertex $ 1 $ is $ 1 $ : there is only one path from $ 1 $ to $ 1 $ (path with length $ 0 $ ); - the answer for vertex $ 2 $ is $ 0 $ : there are no paths from $ 1 $ to $ 2 $ ; - the answer for vertex $ 3 $ is $ 1 $ : there is only one path from $ 1 $ to $ 3 $ (it is the edge $ (1, 3) $ ); - the answer for vertex $ 4 $ is $ 2 $ : there are more than one paths from $ 1 $ to $ 4 $ and the number of paths are finite (two paths: $ [(1, 3), (3, 4)] $ and $ [(1, 4)] $ ); - the answer for vertex $ 5 $ is $ -1 $ : the number of paths from $ 1 $ to $ 5 $ is infinite (the loop can be used in a path many times); - the answer for vertex $ 6 $ is $ -1 $ : the number of paths from $ 1 $ to $ 6 $ is infinite (the loop can be used in a path many times).

输入输出格式

输入格式

The first contains an integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases in the input. Then $ t $ test cases follow. Before each test case, there is an empty line. The first line of the test case contains two integers $ n $ and $ m $ ( $ 1 \le n \le 4 \cdot 10^5, 0 \le m \le 4 \cdot 10^5 $ ) — numbers of vertices and edges in graph respectively. The next $ m $ lines contain edges descriptions. Each line contains two integers $ a_i $ , $ b_i $ ( $ 1 \le a_i, b_i \le n $ ) — the start and the end of the $ i $ -th edge. The vertices of the graph are numbered from $ 1 $ to $ n $ . The given graph can contain loops (it is possible that $ a_i = b_i $ ), but cannot contain multi-edges (it is not possible that $ a_i = a_j $ and $ b_i = b_j $ for $ i \ne j $ ). The sum of $ n $ over all test cases does not exceed $ 4 \cdot 10^5 $ . Similarly, the sum of $ m $ over all test cases does not exceed $ 4 \cdot 10^5 $ .

输出格式

Output $ t $ lines. The $ i $ -th line should contain an answer for the $ i $ -th test case: a sequence of $ n $ integers from $ -1 $ to $ 2 $ .

输入输出样例

输入样例 #1

5

6 7
1 4
1 3
3 4
4 5
2 1
5 5
5 6

1 0

3 3
1 2
2 3
3 1

5 0

4 4
1 2
2 3
1 4
4 3

输出样例 #1

1 0 1 2 -1 -1 
1 
-1 -1 -1 
1 0 0 0 0 
1 1 2 1