Gardener and Tree

题意翻译

### 题目描述 一棵 $n$ 个结点的树。一个人做了多次操作，在每次操作中，他删除了树的所有叶子结点。  如上图中所示的树。下图显示了对树进行一次操作后的结果。  注意特殊操作的情况: 1、对空树($0$ 个顶点)进行操作时不会改变它; 2、对一个顶点的树进行操作时会移除这个顶点(这个顶点被当作一个叶子); 3、对有两个顶点的树进行操作时将删除两个顶点(两个顶点都被当作叶子处理)。 求 $k$ 次操作后还剩下多少个顶点? ### 输入格式 第一行包含一个整数 $T$。然后是 $T$ 组测试数据。 对于每组测试数据，共 $n$ 行：第一行包含两个整数 $n$和 $k$——树中的顶点数和操作次数。然后是 $n−1$ 行，每一行包含两个整数 $u$ 和 $v$ ($1\le u,v≤n，u \ne v$)，表示一条无向边。保证是一个树，且每两组测试数据中间有一个换行。 ### 输出格式 共 $T$ 行，每行一个正整数 $ans$，表示每组数据的答案。

题目描述

A tree is an undirected connected graph in which there are no cycles. This problem is about non-rooted trees. A leaf of a tree is a vertex that is connected to at most one vertex. The gardener Vitaly grew a tree from $ n $ vertices. He decided to trim the tree. To do this, he performs a number of operations. In one operation, he removes all leaves of the tree. 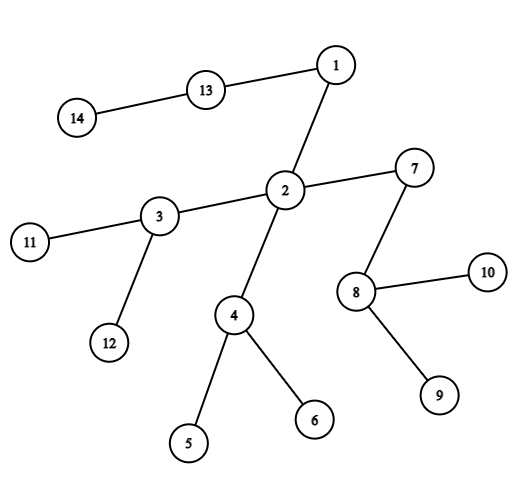Example of a tree.For example, consider the tree shown in the figure above. The figure below shows the result of applying exactly one operation to the tree. 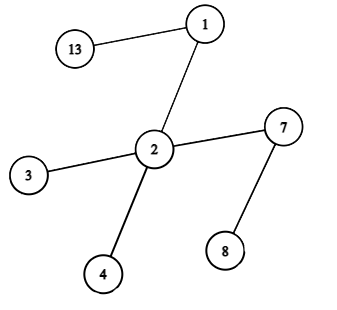The result of applying the operation "remove all leaves" to the tree.Note the special cases of the operation: - applying an operation to an empty tree (of $ 0 $ vertices) does not change it; - applying an operation to a tree of one vertex removes this vertex (this vertex is treated as a leaf); - applying an operation to a tree of two vertices removes both vertices (both vertices are treated as leaves). Vitaly applied $ k $ operations sequentially to the tree. How many vertices remain?

输入输出格式

输入格式

The first line contains one integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases. Then $ t $ test cases follow. Each test case is preceded by an empty line. Each test case consists of several lines. The first line of the test case contains two integers $ n $ and $ k $ ( $ 1 \le n \le 4 \cdot 10^5 $ , $ 1 \le k \le 2 \cdot 10^5 $ ) — the number of vertices in the tree and the number of operations, respectively. Then $ n - 1 $ lines follow, each of them contains two integers $ u $ and $ v $ ( $ 1 \le u, v \le n $ , $ u \neq v $ ) which describe a pair of vertices connected by an edge. It is guaranteed that the given graph is a tree and has no loops or multiple edges. It is guaranteed that the sum of $ n $ from all test cases does not exceed $ 4 \cdot 10^5 $ .

输出格式

For each test case output on a separate line a single integer — the number of vertices that remain in the tree after applying $ k $ operations.

输入输出样例

输入样例 #1

6

14 1
1 2
2 3
2 4
4 5
4 6
2 7
7 8
8 9
8 10
3 11
3 12
1 13
13 14

2 200000
1 2

3 2
1 2
2 3

5 1
5 1
3 2
2 1
5 4

6 2
5 1
2 5
5 6
4 2
3 4

7 1
4 3
5 1
1 3
6 1
1 7
2 1

输出样例 #1

7
0
0
3
1
2

说明

The first test case is considered in the statement. The second test case contains a tree of two vertices. $ 200000 $ operations are applied to it. The first one removes all two vertices, the other operations do not change the tree. In the third test case, a tree of three vertices is given. As a result of the first operation, only $ 1 $ vertex remains in it (with the index $ 2 $ ), the second operation makes the tree empty.