Rubik's Cube Coloring (hard version)

题意翻译

有一棵深度为 $k$ 的满二叉树（根节点深度为 $1$）。 你要用 $6$ 种颜色去染色，使得相邻节点颜色不同，并且也不会是魔方对面的两个面的颜色。 具体来说： - 如果一个节点是白色的，那么相邻节点不能是白色的或黄色的。 - 如果一个节点是黄色的，那么相邻节点不能是白色的或黄色的。 - 如果一个节点是绿色的，那么相邻节点不能是绿色的或蓝色的。 - 如果一个节点是蓝色的，那么相邻节点不能是绿色的或蓝色的。 - 如果一个节点是红色的，那么相邻节点不能是红色的或橙色的。 - 如果一个节点是橙色的，那么相邻节点不能是红色的或橙色的。 现在已知了 $n$ 个节点的颜色信息（在 E1 中为 0），求给整棵树染色的方案数。

题目描述

It is the hard version of the problem. The difference is that in this version, there are nodes with already chosen colors. Theofanis is starving, and he wants to eat his favorite food, sheftalia. However, he should first finish his homework. Can you help him with this problem? You have a perfect binary tree of $ 2^k - 1 $ nodes — a binary tree where all vertices $ i $ from $ 1 $ to $ 2^{k - 1} - 1 $ have exactly two children: vertices $ 2i $ and $ 2i + 1 $ . Vertices from $ 2^{k - 1} $ to $ 2^k - 1 $ don't have any children. You want to color its vertices with the $ 6 $ Rubik's cube colors (White, Green, Red, Blue, Orange and Yellow). Let's call a coloring good when all edges connect nodes with colors that are neighboring sides in the Rubik's cube. 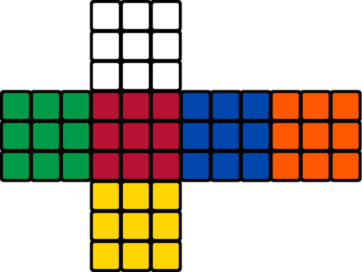A picture of Rubik's cube and its 2D map.More formally: - a white node can not be neighboring with white and yellow nodes; - a yellow node can not be neighboring with white and yellow nodes; - a green node can not be neighboring with green and blue nodes; - a blue node can not be neighboring with green and blue nodes; - a red node can not be neighboring with red and orange nodes; - an orange node can not be neighboring with red and orange nodes; However, there are $ n $ special nodes in the tree, colors of which are already chosen. You want to calculate the number of the good colorings of the binary tree. Two colorings are considered different if at least one node is colored with a different color. The answer may be too large, so output the answer modulo $ 10^9+7 $ .

输入输出格式

输入格式

The first line contains the integers $ k $ ( $ 1 \le k \le 60 $ ) — the number of levels in the perfect binary tree you need to color. The second line contains the integer $ n $ ( $ 1 \le n \le \min(2^k - 1, 2000) $ ) — the number of nodes, colors of which are already chosen. The next $ n $ lines contains integer $ v $ ( $ 1 \le v \le 2^k - 1 $ ) and string $ s $ — the index of the node and the color of the node ( $ s $ is one of the white, yellow, green, blue, red and orange). It is guaranteed that each node $ v $ appears in the input at most once.

输出格式

Print one integer — the number of the different colorings modulo $ 10^9+7 $ .

输入输出样例

输入样例 #1

3
2
5 orange
2 white

输出样例 #1

1024

输入样例 #2

2
2
1 white
2 white

输出样例 #2

0

输入样例 #3

10
3
1 blue
4 red
5 orange

输出样例 #3

328925088

说明

In the picture below, you can see one of the correct colorings of the first test example. 

题意翻译

有一棵深度为 $k$ 的满二叉树（根节点深度为 $1$）。 你要用 $6$ 种颜色去染色，使得相邻节点颜色不同，并且也不会是魔方对面的两个面的颜色。 具体来说： - 如果一个节点是白色的，那么相邻节点不能是白色的或黄色的。 - 如果一个节点是黄色的，那么相邻节点不能是白色的或黄色的。 - 如果一个节点是绿色的，那么相邻节点不能是绿色的或蓝色的。 - 如果一个节点是蓝色的，那么相邻节点不能是绿色的或蓝色的。 - 如果一个节点是红色的，那么相邻节点不能是红色的或橙色的。 - 如果一个节点是橙色的，那么相邻节点不能是红色的或橙色的。 现在已知了 $n$ 个节点的颜色信息（在 E1 中为 0），求给整棵树染色的方案数。