Not Assigning

题意翻译

你有一棵包含 $n$ 个点的树，第 $i$ 条边连接点 $u_i$ 和点 $v_i$，请给所有 $n-1$ 条边分配一个权值，使得树上任意两点之间最多包含两条边的路径上的所有边的权值和为质数。如果不存在满足要求的权值分配方案，输出 `-1`。 可以证明，如果存在一组权值分配方案，所有边的权值都在 $[1,10^5]$ 以内。 数据范围： - $t$ 组数据，$1\leqslant t\leqslant 10^4$。 - $2\leqslant n\leqslant 10^5$。 - $1\leqslant u_i,v_i\leqslant n$。 Translated by Eason_AC 2022.1.19

题目描述

You are given a tree of $ n $ vertices numbered from $ 1 $ to $ n $ , with edges numbered from $ 1 $ to $ n-1 $ . A tree is a connected undirected graph without cycles. You have to assign integer weights to each edge of the tree, such that the resultant graph is a prime tree. A prime tree is a tree where the weight of every path consisting of one or two edges is prime. A path should not visit any vertex twice. The weight of a path is the sum of edge weights on that path. Consider the graph below. It is a prime tree as the weight of every path of two or less edges is prime. For example, the following path of two edges: $ 2 \to 1 \to 3 $ has a weight of $ 11 + 2 = 13 $ , which is prime. Similarly, the path of one edge: $ 4 \to 3 $ has a weight of $ 5 $ , which is also prime. 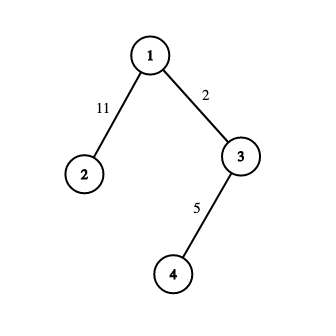Print any valid assignment of weights such that the resultant tree is a prime tree. If there is no such assignment, then print $ -1 $ . It can be proven that if a valid assignment exists, one exists with weights between $ 1 $ and $ 10^5 $ as well.

输入输出格式

输入格式

The input consists of multiple test cases. The first line contains an integer $ t $ ( $ 1 \leq t \leq 10^4 $ ) — the number of test cases. The description of the test cases follows. The first line of each test case contains one integer $ n $ ( $ 2 \leq n \leq 10^5 $ ) — the number of vertices in the tree. Then, $ n-1 $ lines follow. The $ i $ -th line contains two integers $ u $ and $ v $ ( $ 1 \leq u, v \leq n $ ) denoting that edge number $ i $ is between vertices $ u $ and $ v $ . It is guaranteed that the edges form a tree. It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 10^5 $ .

输出格式

For each test case, if a valid assignment exists, then print a single line containing $ n-1 $ integers $ a_1, a_2, \dots, a_{n-1} $ ( $ 1 \leq a_i \le 10^5 $ ), where $ a_i $ denotes the weight assigned to the edge numbered $ i $ . Otherwise, print $ -1 $ . If there are multiple solutions, you may print any.

输入输出样例

输入样例 #1

3
2
1 2
4
1 3
4 3
2 1
7
1 2
1 3
3 4
3 5
6 2
7 2

输出样例 #1

17
2 5 11
-1

说明

For the first test case, there are only two paths having one edge each: $ 1 \to 2 $ and $ 2 \to 1 $ , both having a weight of $ 17 $ , which is prime. The second test case is described in the statement. It can be proven that no such assignment exists for the third test case.