Not Escaping

题意翻译

### 题目描述 有一 $n$ 行 $m$ 列的网格，$(i,j)$ 表示第 $i$ 行的第 $j$ 格。有人要从 $(1,1)$ 走到 $(n,m)$。在同一行，可以任意向左或右移动，且从 $(i,j)$ 到 $(i,k)$ 需要损失 $\left|j-k\right|\times x_i$ 的生命值。但是他无法从某一行直接走到另一行。网格中有 $k$ 架梯子，每架梯子可以让他从 $(a_i,b_i)$ **单向** 移动到 $(c_i,d_i)$（满足 $a_i<c_i$），并获得 $h_i$ 的生命值。请输出所有可以走的路径中 **损失** 的生命值的最小值（若该值为负数说明他在逃脱后反而能增加生命值）；若不可能走到，输出"NO ESCAPE"。 ### 输入格式及数据范围 第一行一个 $t\ (1\le t\le 5\times10^4)$ ，表示一共有 $t$ 组数据。 接下来依次输入 $t$ 组数据。每组数据的第一行有 3 个整数：$n,m,k\ (2\le n,m\le 10^5;1\le k\le 10^5)$； 第二行 $n$ 个数，表示 $x_1\sim x_n\ (1\le x_i\le10^6)$； 接下来 $k$ 行每行 5 个数，表示每架梯子的参数 $a_i,b_i,c_i,d_i,h_i\ (1\le a_i<c_i\le n;1\le b_i,d_i\le m;1\le h_i\le 10^6)$。 保证每个 $a_i<c_i$，且每两格间最多一架梯子。保证所有数据的 $n,m,k$ 的和分别都 $\le 10^5$。 ### 样例解释 第一组数据如图，有两条路径： 第一条是：$(1,1)\rightarrow (1,3)\rightarrow (3,3)\rightarrow(3,2)\rightarrow(5,1)\rightarrow(5,3)$，消耗的生命值为： $$x_1\cdot\left|1-3\right|-h_1+x_3\cdot\left|3-2\right|-h_3+x_5\cdot\left|1-3\right| = 16$$ 第二条是：$(1,1)\rightarrow (1,3)\rightarrow (3,3)\rightarrow(3,1)\rightarrow(5,2)\rightarrow(5,3)$，消耗的生命值为： $$x_1\cdot\left|1-3\right|-h_1+x_3\cdot\left|3-1\right|-h_2+x_5\cdot\left|2-3\right| = 21$$ 故最小值为 $16$。 第二组数据没有从 $(1,1)$ 到 $(n,m)$ 的路径。 第三组数据的路径只能为：$(1,1)\rightarrow(1,3)\rightarrow(5,3)$，消耗生命值为$5\times2-100 = -90$，表示他经过这条路后能增加 $90$ 生命值。

题目描述

Major Ram is being chased by his arch enemy Raghav. Ram must reach the top of the building to escape via helicopter. The building, however, is on fire. Ram must choose the optimal path to reach the top of the building to lose the minimum amount of health. The building consists of $ n $ floors, each with $ m $ rooms each. Let $ (i, j) $ represent the $ j $ -th room on the $ i $ -th floor. Additionally, there are $ k $ ladders installed. The $ i $ -th ladder allows Ram to travel from $ (a_i, b_i) $ to $ (c_i, d_i) $ , but not in the other direction. Ram also gains $ h_i $ health points if he uses the ladder $ i $ . It is guaranteed $ a_i < c_i $ for all ladders. If Ram is on the $ i $ -th floor, he can move either left or right. Travelling across floors, however, is treacherous. If Ram travels from $ (i, j) $ to $ (i, k) $ , he loses $ |j-k| \cdot x_i $ health points. Ram enters the building at $ (1, 1) $ while his helicopter is waiting at $ (n, m) $ . What is the minimum amount of health Ram loses if he takes the most optimal path? Note this answer may be negative (in which case he gains health). Output "NO ESCAPE" if no matter what path Ram takes, he cannot escape the clutches of Raghav.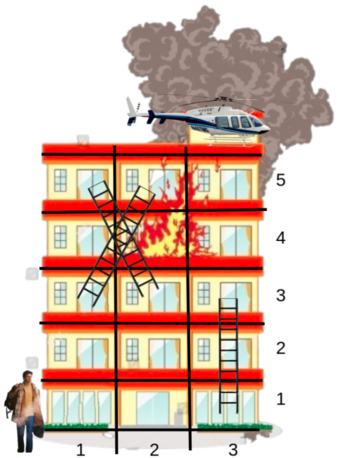 

输入输出格式

输入格式

The first line of input contains $ t $ ( $ 1 \leq t \leq 5 \cdot 10^4 $ ) — the number of test cases. The first line of each test case consists of $ 3 $ integers $ n, m, k $ ( $ 2 \leq n, m \leq 10^5 $ ; $ 1 \leq k \leq 10^5 $ ) — the number of floors, the number of rooms on each floor and the number of ladders respectively. The second line of a test case consists of $ n $ integers $ x_1, x_2, \dots, x_n $ ( $ 1 \leq x_i \leq 10^6 $ ). The next $ k $ lines describe the ladders. Ladder $ i $ is denoted by $ a_i, b_i, c_i, d_i, h_i $ ( $ 1 \leq a_i < c_i \leq n $ ; $ 1 \leq b_i, d_i \leq m $ ; $ 1 \leq h_i \leq 10^6 $ ) — the rooms it connects and the health points gained from using it. It is guaranteed $ a_i < c_i $ for all ladders and there is at most one ladder between any 2 rooms in the building. The sum of $ n $ , the sum of $ m $ , and the sum of $ k $ over all test cases do not exceed $ 10^5 $ .

输出格式

Output the minimum health Ram loses on the optimal path from $ (1, 1) $ to $ (n, m) $ . If Ram cannot escape the clutches of Raghav regardless of the path he takes, output "NO ESCAPE" (all uppercase, without quotes).

输入输出样例

输入样例 #1

4
5 3 3
5 17 8 1 4
1 3 3 3 4
3 1 5 2 5
3 2 5 1 6
6 3 3
5 17 8 1 4 2
1 3 3 3 4
3 1 5 2 5
3 2 5 1 6
5 3 1
5 17 8 1 4
1 3 5 3 100
5 5 5
3 2 3 7 5
3 5 4 2 1
2 2 5 4 5
4 4 5 2 3
1 2 4 2 2
3 3 5 2 4

输出样例 #1

16
NO ESCAPE
-90
27

说明

The figure for the first test case is in the statement. There are only $ 2 $ possible paths to $ (n, m) $ : - Ram travels to $ (1, 3) $ , takes the ladder to $ (3, 3) $ , travels to $ (3, 2) $ , takes the ladder to $ (5, 1) $ , travels to $ (5, 3) $ where he finally escapes via helicopter. The health lost would be $ $ \begin{align*} &\mathrel{\phantom{=}} x_1 \cdot |1-3| - h_1 + x_3 \cdot |3-2| - h_3 + x_5 \cdot |1-3| \\ &= 5 \cdot 2 - 4 + 8 \cdot 1 - 6 + 4 \cdot 2 \\ &= 16. \end{align*} $ $ </li><li> Ram travels to $ (1, 3) $ , takes the ladder to $ (3, 3) $ , travels to $ (3, 1) $ , takes the ladder to $ (5, 2) $ , travels to $ (5, 3) $ where he finally escapes via helicopter. The health lost would be $ $ \begin{align*} &\mathrel{\phantom{=}} x_1 \cdot |1-3| - h_1 + x_3 \cdot |3-1| - h_2 + a_5 \cdot |2-3| \\ &= 5 \cdot 2 - 4 + 8 \cdot 2 - 5 + 4 \cdot 1 \\ &= 21. \end{align*} $ $ </li></ul> Therefore, the minimum health lost would be $ 16 $ .<p>In the second test case, there is no path to $ (n, m) $ .</p><p>In the third case case, Ram travels to $ (1, 3) $ and takes the only ladder to $ (5, 3) $ . He loses $ 5 \\cdot 2 $ health points and gains $ h\_1 = 100 $ health points. Therefore the total loss is $ 10-100=-90$ (negative implies he gains health after the path).