309456: CF1681E. Labyrinth Adventures
Memory Limit:512 MB
Time Limit:6 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Labyrinth Adventures
题意翻译
#### 题目描述 有一个 $n\times n$ 的方格图,坐标编号类似平面直角坐标系,左下角为 $(1, 1)$。 这个方格图被分成了 $n$ 层,左下角 $(1, 1)$ 为第一层,随后每层都向外拓展一圈,如下图就是 $n=5$ 的时候的情况: 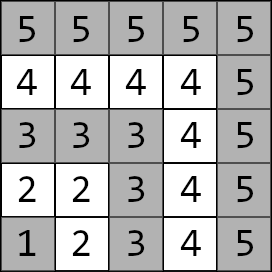 层于层之间有墙隔开,但每层都有两个门,分别分布在该层顶部和右侧,门是双向的。 现在给出这些门的坐标,有 $m$ 次询问,每次给定两个坐标 $(x_1, y_1)$ 和 $(x_2,y_2)$,请你回答两点之间的最短路。 #### 输入格式 第一行一个 $n$。 接下来的 $n-1$ 行中,每行有四个整数 $d_{1,x}, d_{1,y}, d_{2,x}, d_{2,y}$,第 $i$ 行表示第 $i$ 层的两个门的坐标。前两个表示顶部门坐标,后两个表示右侧门坐标。 下一行输入 $m$。 接下来 $m$ 行,每行四个整数,$x_1,y_1,x_2,y_2$,含义如题目描述。 #### 输出格式 对每次询问,输出一行一个整数,表示两点之间的最短路长度。**长度的定义是移动的步数。** #### 样例解释 下图是样例二的网格图,红色的是门。 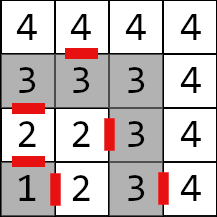题目描述
You found a map of a weirdly shaped labyrinth. The map is a grid, consisting of $ n $ rows and $ n $ columns. The rows of the grid are numbered from $ 1 $ to $ n $ from bottom to top. The columns of the grid are numbered from $ 1 $ to $ n $ from left to right. The labyrinth has $ n $ layers. The first layer is the bottom left corner (cell $ (1, 1) $ ). The second layer consists of all cells that are in the grid and adjacent to the first layer by a side or a corner. The third layer consists of all cells that are in the grid and adjacent to the second layer by a side or a corner. And so on. The labyrinth with $ 5 $ layers, for example, is shaped as follows: 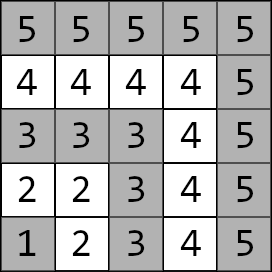The layers are separated from one another with walls. However, there are doors in these walls. Each layer (except for layer $ n $ ) has exactly two doors to the next layer. One door is placed on the top wall of the layer and another door is placed on the right wall of the layer. For each layer from $ 1 $ to $ n-1 $ you are given positions of these two doors. The doors can be passed in both directions: either from layer $ i $ to layer $ i+1 $ or from layer $ i+1 $ to layer $ i $ . If you are standing in some cell, you can move to an adjacent by a side cell if a wall doesn't block your move (e.g. you can't move to a cell in another layer if there is no door between the cells). Now you have $ m $ queries of sort: what's the minimum number of moves one has to make to go from cell $ (x_1, y_1) $ to cell $ (x_2, y_2) $ .输入输出格式
输入格式
The first line contains a single integer $ n $ ( $ 2 \le n \le 10^5 $ ) — the number of layers in the labyrinth. The $ i $ -th of the next $ n-1 $ lines contains four integers $ d_{1,x}, d_{1,y}, d_{2,x} $ and $ d_{2,y} $ ( $ 1 \le d_{1,x}, d_{1,y}, d_{2,x}, d_{2,y} \le n $ ) — the coordinates of the doors. Both cells are on the $ i $ -th layer. The first cell is adjacent to the top wall of the $ i $ -th layer by a side — that side is where the door is. The second cell is adjacent to the right wall of the $ i $ -th layer by a side — that side is where the door is. The next line contains a single integer $ m $ ( $ 1 \le m \le 2 \cdot 10^5 $ ) — the number of queries. The $ j $ -th of the next $ m $ lines contains four integers $ x_1, y_1, x_2 $ and $ y_2 $ ( $ 1 \le x_1, y_1, x_2, y_2 \le n $ ) — the coordinates of the cells in the $ j $ -th query.
输出格式
For each query, print a single integer — the minimum number of moves one has to make to go from cell $ (x_1, y_1) $ to cell $ (x_2, y_2) $ .
输入输出样例
输入样例 #1
2
1 1 1 1
10
1 1 1 1
1 1 1 2
1 1 2 1
1 1 2 2
1 2 1 2
1 2 2 1
1 2 2 2
2 1 2 1
2 1 2 2
2 2 2 2输出样例 #1
0
1
1
2
0
2
1
0
1
0输入样例 #2
4
1 1 1 1
2 1 2 2
3 2 1 3
5
2 4 4 3
4 4 3 3
1 2 3 3
2 2 4 4
1 4 2 3输出样例 #2
3
4
3
6
2说明
Here is the map of the labyrinth from the second example. The doors are marked red. 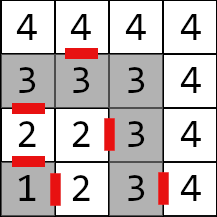Input
题意翻译
#### 题目描述 有一个 $n\times n$ 的方格图,坐标编号类似平面直角坐标系,左下角为 $(1, 1)$。 这个方格图被分成了 $n$ 层,左下角 $(1, 1)$ 为第一层,随后每层都向外拓展一圈,如下图就是 $n=5$ 的时候的情况:  层于层之间有墙隔开,但每层都有两个门,分别分布在该层顶部和右侧,门是双向的。 现在给出这些门的坐标,有 $m$ 次询问,每次给定两个坐标 $(x_1, y_1)$ 和 $(x_2,y_2)$,请你回答两点之间的最短路。 #### 输入格式 第一行一个 $n$。 接下来的 $n-1$ 行中,每行有四个整数 $d_{1,x}, d_{1,y}, d_{2,x}, d_{2,y}$,第 $i$ 行表示第 $i$ 层的两个门的坐标。前两个表示顶部门坐标,后两个表示右侧门坐标。 下一行输入 $m$。 接下来 $m$ 行,每行四个整数,$x_1,y_1,x_2,y_2$,含义如题目描述。 #### 输出格式 对每次询问,输出一行一个整数,表示两点之间的最短路长度。**长度的定义是移动的步数。** #### 样例解释 下图是样例二的网格图,红色的是门。 Output
**迷宫冒险**
#### 题目描述
有一个 $n \times n$ 的方格图,坐标编号类似平面直角坐标系,左下角为 $(1, 1)$。
这个方格图被分成了 $n$ 层,左下角 $(1, 1)$ 为第一层,随后每层都向外拓展一圈。
层与层之间有墙隔开,但每层都有两个门,分别分布在该层顶部和右侧,门是双向的。
现在给出这些门的坐标,有 $m$ 次询问,每次给定两个坐标 $(x_1, y_1)$ 和 $(x_2, y_2)$,请你回答两点之间的最短路。
#### 输入格式
第一行一个 $n$。
接下来的 $n-1$ 行中,每行有四个整数 $d_{1,x}, d_{1,y}, d_{2,x}, d_{2,y}$,第 $i$ 行表示第 $i$ 层的两个门的坐标。前两个表示顶部门坐标,后两个表示右侧门坐标。
下一行输入 $m$。
接下来 $m$ 行,每行四个整数,$x_1, y_1, x_2, y_2$,含义如题目描述。
#### 输出格式
对每次询问,输出一行一个整数,表示两点之间的最短路长度。
#### 样例解释
下图是样例二的网格图,红色的是门。

---
**题目描述**
你发现了一个奇形怪状的迷宫的地图。地图是一个由 $n$ 行和 $n$ 列组成的网格。网格的行从下到上编号为 $1$ 到 $n$。网格的列从左到右编号为 $1$ 到 $n$。
迷宫有 $n$ 层。第一层是左下角的单元格 $(1, 1)$。第二层包括网格中与第一层相邻的单元格(通过边或角)。第三层包括网格中与第二层相邻的单元格(通过边或角)。依此类推。
例如,具有 $5$ 层的迷宫形状如下:

层与层之间有墙隔开。然而,这些墙上有门。
除了第 $n$ 层之外的每一层都有两个通向下一层的门。一个门位于层的顶部墙上,另一个门位于层的右侧墙上。对于从 $1$ 到 $n-1$ 的每一层,你都会得到这些门的位置。门可以从两个方向通过:从层 $i$ 到层 $i+1$,或者从层 $i+1$ 到层 $i$。
如果你站在某个单元格中,你可以移动到通过边相邻的单元格,除非墙阻挡了你的移动(例如,如果你不能移动到另一个层的单元格,如果没有门连接这些单元格)。
现在你有 $m$ 次查询,询问从单元格 $(x_1, y_1)$ 到单元格 $(x_2, y_2)$ 需要的最少移动次数。
#### 输入输出格式
**输入格式**
第一行包含一个整数 $n$ ($2 \le n \le 10^5$) — 迷宫中的层数。
接下来的 $n-1$ 行中,第 $i$ 行包含四个整数 $d_{1,x}, d_{1,y}, d_{2,x}$ 和 $d_{2,y}$ ($1 \le d_{1,x}, d_{1,y}, d_{2,x}, d_{2,y} \le n$) — 门的坐标。两个单元格都在第 $i$ 层。第一个单元格通过边与第 $i$ 层的顶部墙相邻,那里有门。第二个单元格通过边与第 $i$ 层的右侧墙相邻,那里有门。
下一行包含一个整数 $m$ ($1 \le m \le 2 \cdot 10^5$) — 查询的数量。
接下来的 $m$ 行中,第 $j$ 行包含四个整数 $x_1, y_1, x_2, y_2$ ($1 \le x_1, y_1, x_2, y_2 \le n$) — 第 $j$ 个查询中单元格的坐标。
**输出格式**
对于每个查询,打印一个整数 — 从单元格 $(x_1, y_1)$ 到单元格 $(x**迷宫冒险** #### 题目描述 有一个 $n \times n$ 的方格图,坐标编号类似平面直角坐标系,左下角为 $(1, 1)$。 这个方格图被分成了 $n$ 层,左下角 $(1, 1)$ 为第一层,随后每层都向外拓展一圈。 层与层之间有墙隔开,但每层都有两个门,分别分布在该层顶部和右侧,门是双向的。 现在给出这些门的坐标,有 $m$ 次询问,每次给定两个坐标 $(x_1, y_1)$ 和 $(x_2, y_2)$,请你回答两点之间的最短路。 #### 输入格式 第一行一个 $n$。 接下来的 $n-1$ 行中,每行有四个整数 $d_{1,x}, d_{1,y}, d_{2,x}, d_{2,y}$,第 $i$ 行表示第 $i$ 层的两个门的坐标。前两个表示顶部门坐标,后两个表示右侧门坐标。 下一行输入 $m$。 接下来 $m$ 行,每行四个整数,$x_1, y_1, x_2, y_2$,含义如题目描述。 #### 输出格式 对每次询问,输出一行一个整数,表示两点之间的最短路长度。 #### 样例解释 下图是样例二的网格图,红色的是门。  --- **题目描述** 你发现了一个奇形怪状的迷宫的地图。地图是一个由 $n$ 行和 $n$ 列组成的网格。网格的行从下到上编号为 $1$ 到 $n$。网格的列从左到右编号为 $1$ 到 $n$。 迷宫有 $n$ 层。第一层是左下角的单元格 $(1, 1)$。第二层包括网格中与第一层相邻的单元格(通过边或角)。第三层包括网格中与第二层相邻的单元格(通过边或角)。依此类推。 例如,具有 $5$ 层的迷宫形状如下:  层与层之间有墙隔开。然而,这些墙上有门。 除了第 $n$ 层之外的每一层都有两个通向下一层的门。一个门位于层的顶部墙上,另一个门位于层的右侧墙上。对于从 $1$ 到 $n-1$ 的每一层,你都会得到这些门的位置。门可以从两个方向通过:从层 $i$ 到层 $i+1$,或者从层 $i+1$ 到层 $i$。 如果你站在某个单元格中,你可以移动到通过边相邻的单元格,除非墙阻挡了你的移动(例如,如果你不能移动到另一个层的单元格,如果没有门连接这些单元格)。 现在你有 $m$ 次查询,询问从单元格 $(x_1, y_1)$ 到单元格 $(x_2, y_2)$ 需要的最少移动次数。 #### 输入输出格式 **输入格式** 第一行包含一个整数 $n$ ($2 \le n \le 10^5$) — 迷宫中的层数。 接下来的 $n-1$ 行中,第 $i$ 行包含四个整数 $d_{1,x}, d_{1,y}, d_{2,x}$ 和 $d_{2,y}$ ($1 \le d_{1,x}, d_{1,y}, d_{2,x}, d_{2,y} \le n$) — 门的坐标。两个单元格都在第 $i$ 层。第一个单元格通过边与第 $i$ 层的顶部墙相邻,那里有门。第二个单元格通过边与第 $i$ 层的右侧墙相邻,那里有门。 下一行包含一个整数 $m$ ($1 \le m \le 2 \cdot 10^5$) — 查询的数量。 接下来的 $m$ 行中,第 $j$ 行包含四个整数 $x_1, y_1, x_2, y_2$ ($1 \le x_1, y_1, x_2, y_2 \le n$) — 第 $j$ 个查询中单元格的坐标。 **输出格式** 对于每个查询,打印一个整数 — 从单元格 $(x_1, y_1)$ 到单元格 $(x
#### 题目描述
有一个 $n \times n$ 的方格图,坐标编号类似平面直角坐标系,左下角为 $(1, 1)$。
这个方格图被分成了 $n$ 层,左下角 $(1, 1)$ 为第一层,随后每层都向外拓展一圈。
层与层之间有墙隔开,但每层都有两个门,分别分布在该层顶部和右侧,门是双向的。
现在给出这些门的坐标,有 $m$ 次询问,每次给定两个坐标 $(x_1, y_1)$ 和 $(x_2, y_2)$,请你回答两点之间的最短路。
#### 输入格式
第一行一个 $n$。
接下来的 $n-1$ 行中,每行有四个整数 $d_{1,x}, d_{1,y}, d_{2,x}, d_{2,y}$,第 $i$ 行表示第 $i$ 层的两个门的坐标。前两个表示顶部门坐标,后两个表示右侧门坐标。
下一行输入 $m$。
接下来 $m$ 行,每行四个整数,$x_1, y_1, x_2, y_2$,含义如题目描述。
#### 输出格式
对每次询问,输出一行一个整数,表示两点之间的最短路长度。
#### 样例解释
下图是样例二的网格图,红色的是门。

---
**题目描述**
你发现了一个奇形怪状的迷宫的地图。地图是一个由 $n$ 行和 $n$ 列组成的网格。网格的行从下到上编号为 $1$ 到 $n$。网格的列从左到右编号为 $1$ 到 $n$。
迷宫有 $n$ 层。第一层是左下角的单元格 $(1, 1)$。第二层包括网格中与第一层相邻的单元格(通过边或角)。第三层包括网格中与第二层相邻的单元格(通过边或角)。依此类推。
例如,具有 $5$ 层的迷宫形状如下:

层与层之间有墙隔开。然而,这些墙上有门。
除了第 $n$ 层之外的每一层都有两个通向下一层的门。一个门位于层的顶部墙上,另一个门位于层的右侧墙上。对于从 $1$ 到 $n-1$ 的每一层,你都会得到这些门的位置。门可以从两个方向通过:从层 $i$ 到层 $i+1$,或者从层 $i+1$ 到层 $i$。
如果你站在某个单元格中,你可以移动到通过边相邻的单元格,除非墙阻挡了你的移动(例如,如果你不能移动到另一个层的单元格,如果没有门连接这些单元格)。
现在你有 $m$ 次查询,询问从单元格 $(x_1, y_1)$ 到单元格 $(x_2, y_2)$ 需要的最少移动次数。
#### 输入输出格式
**输入格式**
第一行包含一个整数 $n$ ($2 \le n \le 10^5$) — 迷宫中的层数。
接下来的 $n-1$ 行中,第 $i$ 行包含四个整数 $d_{1,x}, d_{1,y}, d_{2,x}$ 和 $d_{2,y}$ ($1 \le d_{1,x}, d_{1,y}, d_{2,x}, d_{2,y} \le n$) — 门的坐标。两个单元格都在第 $i$ 层。第一个单元格通过边与第 $i$ 层的顶部墙相邻,那里有门。第二个单元格通过边与第 $i$ 层的右侧墙相邻,那里有门。
下一行包含一个整数 $m$ ($1 \le m \le 2 \cdot 10^5$) — 查询的数量。
接下来的 $m$ 行中,第 $j$ 行包含四个整数 $x_1, y_1, x_2, y_2$ ($1 \le x_1, y_1, x_2, y_2 \le n$) — 第 $j$ 个查询中单元格的坐标。
**输出格式**
对于每个查询,打印一个整数 — 从单元格 $(x_1, y_1)$ 到单元格 $(x**迷宫冒险** #### 题目描述 有一个 $n \times n$ 的方格图,坐标编号类似平面直角坐标系,左下角为 $(1, 1)$。 这个方格图被分成了 $n$ 层,左下角 $(1, 1)$ 为第一层,随后每层都向外拓展一圈。 层与层之间有墙隔开,但每层都有两个门,分别分布在该层顶部和右侧,门是双向的。 现在给出这些门的坐标,有 $m$ 次询问,每次给定两个坐标 $(x_1, y_1)$ 和 $(x_2, y_2)$,请你回答两点之间的最短路。 #### 输入格式 第一行一个 $n$。 接下来的 $n-1$ 行中,每行有四个整数 $d_{1,x}, d_{1,y}, d_{2,x}, d_{2,y}$,第 $i$ 行表示第 $i$ 层的两个门的坐标。前两个表示顶部门坐标,后两个表示右侧门坐标。 下一行输入 $m$。 接下来 $m$ 行,每行四个整数,$x_1, y_1, x_2, y_2$,含义如题目描述。 #### 输出格式 对每次询问,输出一行一个整数,表示两点之间的最短路长度。 #### 样例解释 下图是样例二的网格图,红色的是门。  --- **题目描述** 你发现了一个奇形怪状的迷宫的地图。地图是一个由 $n$ 行和 $n$ 列组成的网格。网格的行从下到上编号为 $1$ 到 $n$。网格的列从左到右编号为 $1$ 到 $n$。 迷宫有 $n$ 层。第一层是左下角的单元格 $(1, 1)$。第二层包括网格中与第一层相邻的单元格(通过边或角)。第三层包括网格中与第二层相邻的单元格(通过边或角)。依此类推。 例如,具有 $5$ 层的迷宫形状如下:  层与层之间有墙隔开。然而,这些墙上有门。 除了第 $n$ 层之外的每一层都有两个通向下一层的门。一个门位于层的顶部墙上,另一个门位于层的右侧墙上。对于从 $1$ 到 $n-1$ 的每一层,你都会得到这些门的位置。门可以从两个方向通过:从层 $i$ 到层 $i+1$,或者从层 $i+1$ 到层 $i$。 如果你站在某个单元格中,你可以移动到通过边相邻的单元格,除非墙阻挡了你的移动(例如,如果你不能移动到另一个层的单元格,如果没有门连接这些单元格)。 现在你有 $m$ 次查询,询问从单元格 $(x_1, y_1)$ 到单元格 $(x_2, y_2)$ 需要的最少移动次数。 #### 输入输出格式 **输入格式** 第一行包含一个整数 $n$ ($2 \le n \le 10^5$) — 迷宫中的层数。 接下来的 $n-1$ 行中,第 $i$ 行包含四个整数 $d_{1,x}, d_{1,y}, d_{2,x}$ 和 $d_{2,y}$ ($1 \le d_{1,x}, d_{1,y}, d_{2,x}, d_{2,y} \le n$) — 门的坐标。两个单元格都在第 $i$ 层。第一个单元格通过边与第 $i$ 层的顶部墙相邻,那里有门。第二个单元格通过边与第 $i$ 层的右侧墙相邻,那里有门。 下一行包含一个整数 $m$ ($1 \le m \le 2 \cdot 10^5$) — 查询的数量。 接下来的 $m$ 行中,第 $j$ 行包含四个整数 $x_1, y_1, x_2, y_2$ ($1 \le x_1, y_1, x_2, y_2 \le n$) — 第 $j$ 个查询中单元格的坐标。 **输出格式** 对于每个查询,打印一个整数 — 从单元格 $(x_1, y_1)$ 到单元格 $(x