Print a Pedestal (Codeforces logo?)

题意翻译

**题目描述** 给您一些个数为 $n$ 的方块，请您用这些方块构造一个台座~~CodeForces的徽标~~，每个方块必须都被使用。 这个台座包含三个宽度为 $1$ 格的颁奖台——从左向右依次为第 $2$ 名、第 $1$ 名和第 $3$ 名的位置。 第 $1$ 名的颁奖台必须严格高于第 $2$ 名的颁奖台，第 $2$ 名的颁奖台必须严格高于第 $3$ 名的颁奖台。 此外，每个颁奖台的高度必须大于零（即每个颁奖台必须至少包含一个方块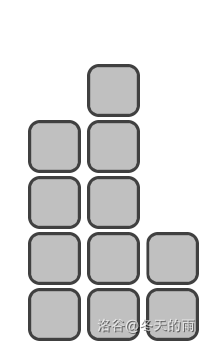）。  如上图所示，我们用 $n = 11$ 个方块构造出了合法的台座：第二名的颁奖台的高度是 $4$，第一名高度是 $5$ 而第三名高度是 $2$ 在所有的可以被构建出的台座中，我们希望让第一名的颁奖台高度**最低**。 如果有多种可能，输出任意一种即可。 **输入格式** 第一行一个整数 $t$ $(1\le t\le 10^4)$ 代表数据组数 下面 $t$ 行，每行一个整数 $n$ $(6\le n\le 10^5)$ 代表可以使用的方块数量。注意所有 $n$ 个方块必须都被使用。 保证一个数据点中所有 $n$ 的和不超过 $10^6$ **输出格式** 对于每一组测试数据，您需要输出三个整数 $h_2$ ，$h_1$ 和 $h_3$ ，代表了每个颁奖台高度。 在所有的可以被构建出的台座中，我们希望让第一名的颁奖台高度最低。 如果有多种可能，输出任意一种即可。 **说明/提示** 在第一组样例中我们不能让第一名的颁奖台台高度小于 $5$ ，因为如果第一名的平台高度不超过 $4$ ，我们最多只可以使用 $4 + 3 + 2 = 9$ 个方块。 当第一名的颁奖台高度是 $5$ 的时候，注意到 $11 = 4 + 5 + 2$ ， 因此答案 $4$ $5$ $2$ 合法。 在第二组样例中只有一种合法答案：$2$ $3$ $1$

题目描述

Given the integer $ n $ — the number of available blocks. You must use all blocks to build a pedestal. The pedestal consists of $ 3 $ platforms for $ 2 $ -nd, $ 1 $ -st and $ 3 $ -rd places respectively. The platform for the $ 1 $ -st place must be strictly higher than for the $ 2 $ -nd place, and the platform for the $ 2 $ -nd place must be strictly higher than for the $ 3 $ -rd place. Also, the height of each platform must be greater than zero (that is, each platform must contain at least one block). 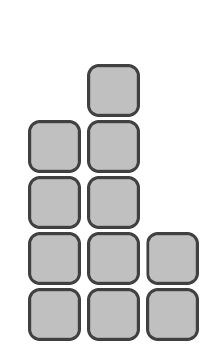Example pedestal of $ n=11 $ blocks: second place height equals $ 4 $ blocks, first place height equals $ 5 $ blocks, third place height equals $ 2 $ blocks.Among all possible pedestals of $ n $ blocks, deduce one such that the platform height for the $ 1 $ -st place minimum as possible. If there are several of them, output any of them.

输入输出格式

输入格式

The first line of input data contains an integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases. Each test case contains a single integer $ n $ ( $ 6 \le n \le 10^5 $ ) — the total number of blocks for the pedestal. All $ n $ blocks must be used. It is guaranteed that the sum of $ n $ values over all test cases does not exceed $ 10^6 $ .

输出格式

For each test case, output $ 3 $ numbers $ h_2, h_1, h_3 $ — the platform heights for $ 2 $ -nd, $ 1 $ -st and $ 3 $ -rd places on a pedestal consisting of $ n $ blocks ( $ h_1+h_2+h_3=n $ , $ 0 < h_3 < h_2 < h_1 $ ). Among all possible pedestals, output the one for which the value of $ h_1 $ minimal. If there are several of them, output any of them.

输入输出样例

输入样例 #1

6
11
6
10
100000
7
8

输出样例 #1

4 5 2
2 3 1
4 5 1
33334 33335 33331
2 4 1
3 4 1

说明

In the first test case we can not get the height of the platform for the first place less than $ 5 $ , because if the height of the platform for the first place is not more than $ 4 $ , then we can use at most $ 4 + 3 + 2 = 9 $ blocks. And we should use $ 11 = 4 + 5 + 2 $ blocks. Therefore, the answer 4 5 2 fits. In the second set, the only suitable answer is: 2 3 1.

**题目大意：**

使用给定数量的方块 $ n $ 构造一个台座，台座由三个分别给第2名、第1名和第3名的颁奖台组成。第1名的颁奖台必须高于第2名的，第2名的必须高于第3名的，每个颁奖台至少需要1个方块。

在所有可能的构造中，要使得第1名的颁奖台高度尽可能低。如果有多种可能，输出任意一种。

**输入格式：**

第一行包含一个整数 $ t $ ，表示测试案例的数量。

接下来 $ t $ 行，每行包含一个整数 $ n $ ，表示可以使用的方块数量。

**输出格式：**

对于每个测试案例，输出三个整数 $ h_2, h_1, h_3 $ ，分别表示第2名、第1名和第3名的颁奖台高度。

**输入输出样例：**

**输入样例 #1：**
```
6
11
6
10
100000
7
8
```

**输出样例 #1：**
```
4 5 2
2 3 1
4 5 1
33334 33335 33331
2 4 1
3 4 1
```

**说明：**

在第一个测试案例中，我们不能让第1名的颁奖台高度小于5，因为如果第1名的颁奖台高度不超过4，最多只能使用9个方块（4 + 3 + 2 = 9），而我们有11个方块，所以答案4 5 2是合法的。

在第二个测试案例中，唯一的合法答案是2 3 1。**题目大意：** 使用给定数量的方块 $ n $ 构造一个台座，台座由三个分别给第2名、第1名和第3名的颁奖台组成。第1名的颁奖台必须高于第2名的，第2名的必须高于第3名的，每个颁奖台至少需要1个方块。 在所有可能的构造中，要使得第1名的颁奖台高度尽可能低。如果有多种可能，输出任意一种。 **输入格式：** 第一行包含一个整数 $ t $ ，表示测试案例的数量。 接下来 $ t $ 行，每行包含一个整数 $ n $ ，表示可以使用的方块数量。 **输出格式：** 对于每个测试案例，输出三个整数 $ h_2, h_1, h_3 $ ，分别表示第2名、第1名和第3名的颁奖台高度。 **输入输出样例：** **输入样例 #1：** ``` 6 11 6 10 100000 7 8 ``` **输出样例 #1：** ``` 4 5 2 2 3 1 4 5 1 33334 33335 33331 2 4 1 3 4 1 ``` **说明：** 在第一个测试案例中，我们不能让第1名的颁奖台高度小于5，因为如果第1名的颁奖台高度不超过4，最多只能使用9个方块（4 + 3 + 2 = 9），而我们有11个方块，所以答案4 5 2是合法的。 在第二个测试案例中，唯一的合法答案是2 3 1。