309513: CF1691F. K-Set Tree
Memory Limit:512 MB
Time Limit:3 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
K-Set Tree
题意翻译
给定一棵有 $n$ 个点的树,定义 $f(r,S) $为以 $r$ 为根时包含集合 $S$ 中所有点的最小子树的大小。 给定常数 $k$ ,对于每一对满足 $|S|=k$ 的 $S$ 和 $r$ ,求所有 $f(r,S)$ 之和,即求 $\sum_{r=1}^{n}\sum_{|S|=k}f(r,S)$题目描述
You are given a tree $ G $ with $ n $ vertices and an integer $ k $ . The vertices of the tree are numbered from $ 1 $ to $ n $ . For a vertex $ r $ and a subset $ S $ of vertices of $ G $ , such that $ |S| = k $ , we define $ f(r, S) $ as the size of the smallest rooted subtree containing all vertices in $ S $ when the tree is rooted at $ r $ . A set of vertices $ T $ is called a rooted subtree, if all the vertices in $ T $ are connected, and for each vertex in $ T $ , all its descendants belong to $ T $ . You need to calculate the sum of $ f(r, S) $ over all possible distinct combinations of vertices $ r $ and subsets $ S $ , where $ |S| = k $ . Formally, compute the following: $ $\sum_{r \in V} \sum_{S \subseteq V, |S| = k} f(r, S), $ $ where $ V $ is the set of vertices in $ G $ .</p><p>Output the answer modulo $ 10^9 + 7$.输入输出格式
输入格式
The first line contains two integers $ n $ and $ k $ ( $ 3 \le n \le 2 \cdot 10^5 $ , $ 1 \le k \le n $ ). Each of the following $ n - 1 $ lines contains two integers $ x $ and $ y $ ( $ 1 \le x, y \le n $ ), denoting an edge between vertex $ x $ and $ y $ . It is guaranteed that the given edges form a tree.
输出格式
Print the answer modulo $ 10^9 + 7 $ .
输入输出样例
输入样例 #1
3 2
1 2
1 3输出样例 #1
25输入样例 #2
7 2
1 2
2 3
2 4
1 5
4 6
4 7输出样例 #2
849说明
The tree in the second example is given below: 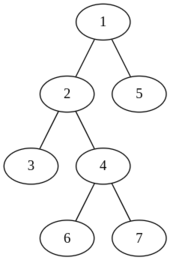We have $ 21 $ subsets of size $ 2 $ in the given tree. Hence, $ $S \in \left\{\{1, 2\}, \{1, 3\}, \{1, 4\}, \{1, 5\}, \{1, 6\}, \{1, 7\}, \{2, 3\}, \{2, 4\}, \{2, 5\}, \{2, 6\}, \{2, 7\}, \{3, 4\}, \{3, 5\}, \{3, 6\}, \{3, 7\}, \{4, 5\}, \{4, 6\}, \{4, 7\}, \{5, 6\}, \{5, 7\}, \{6, 7\} \right\}. $ $ And since we have $ 7 $ vertices, $ 1 \\le r \\le 7 $ . We need to find the sum of $ f(r, S) $ over all possible pairs of $ r $ and $ S $ . </p><p>Below we have listed the value of $ f(r, S) $ for some combinations of $ r $ and $ S $ .</p><ul> <li> $ r = 1 $ , $ S = \\{3, 7\\} $ . The value of $ f(r, S) $ is $ 5 $ and the corresponding subtree is $ \\{2, 3, 4, 6, 7\\} $ . </li><li> $ r = 1 $ , $ S = \\{5, 4\\} $ . The value of $ f(r, S) $ is $ 7 $ and the corresponding subtree is $ \\{1, 2, 3, 4, 5, 6, 7\\} $ . </li><li> $ r = 1 $ , $ S = \\{4, 6\\} $ . The value of $ f(r, S) $ is $ 3 $ and the corresponding subtree is $ \\{4, 6, 7\\}$.Input
题意翻译
给定一棵有 $n$ 个点的树,定义 $f(r,S) $为以 $r$ 为根时包含集合 $S$ 中所有点的最小子树的大小。 给定常数 $k$ ,对于每一对满足 $|S|=k$ 的 $S$ 和 $r$ ,求所有 $f(r,S)$ 之和,即求 $\sum_{r=1}^{n}\sum_{|S|=k}f(r,S)$Output
**K-Set Tree**
**题意翻译**
给定一棵有 $n$ 个点的树,定义 $f(r,S)$ 为以 $r$ 为根时包含集合 $S$ 中所有点的最小子树的大小。
给定常数 $k$ ,对于每一对满足 $|S|=k$ 的 $S$ 和 $r$ ,求所有 $f(r,S)$ 之和,即求
$\sum_{r=1}^{n}\sum_{|S|=k}f(r,S)$
**题目描述**
你有一棵 $n$ 个顶点的树 $G$ 和一个整数 $k$ 。树的顶点编号从 $1$ 到 $n$ 。
对于顶点 $r$ 和树 $G$ 的顶点的一个子集 $S$ ,使得 $|S| = k$ ,我们定义 $f(r, S)$ 为当树以 $r$ 为根时,包含 $S$ 中所有顶点的最小根子树的大小。如果一棵树的顶点集合 $T$ 是连通的,并且对于 $T$ 中的每个顶点,它的所有后裔都属于 $T$ ,则称 $T$ 为根子树。
你需要计算所有可能的顶点 $r$ 和子集 $S$ 的组合的 $f(r, S)$ 之和,其中 $|S| = k$ 。形式上,计算以下内容:
$\sum_{r \in V} \sum_{S \subseteq V, |S| = k} f(r, S),$
其中 $V$ 是树 $G$ 中的顶点集合。
输出答案对 $10^9 + 7$ 取模的结果。
**输入输出格式**
**输入格式**
第一行包含两个整数 $n$ 和 $k$ ($3 \le n \le 2 \cdot 10^5$,$1 \le k \le n$)。
接下来的 $n - 1$ 行,每行包含两个整数 $x$ 和 $y$ ($1 \le x, y \le n$),表示顶点 $x$ 和 $y$ 之间的一条边。
保证给定的边构成一棵树。
**输出格式**
输出答案对 $10^9 + 7$ 取模的结果。
**输入输出样例**
**输入样例 #1**
```
3 2
1 2
1 3
```
**输出样例 #1**
```
25
```
**输入样例 #2**
```
7 2
1 2
2 3
2 4
1 5
4 6
4 7
```
**输出样例 #2**
```
849
```
**说明**
第二个例子中的树如下所示:

在给定的树中,我们有 $21$ 个大小为 $2$ 的子集。因此,$S$ 属于以下集合:
\{\{1, 2\}, \{1, 3\}, \{1, 4\}, \{1, 5\}, \{1, 6\}, \{1, 7\}, \{2, 3\}, \{2, 4\}, \{2, 5\}, \{2, 6\}, \{2, 7\}, \{3, 4\}, \{3, 5\}, \{3, 6\}, \{3, 7\}, \{4, 5\}, \{4, 6\}, \{4, 7\}, \{5, 6\}, \{5, 7\}, \{6, 7\}\}.
并且由于我们有 $7$ 个顶点,$1 \le r \le 7$。我们需要找到所有可能的 $r$ 和 $S$ 对的 $f(r, S)$ 之和。**K-Set Tree** **题意翻译** 给定一棵有 $n$ 个点的树,定义 $f(r,S)$ 为以 $r$ 为根时包含集合 $S$ 中所有点的最小子树的大小。 给定常数 $k$ ,对于每一对满足 $|S|=k$ 的 $S$ 和 $r$ ,求所有 $f(r,S)$ 之和,即求 $\sum_{r=1}^{n}\sum_{|S|=k}f(r,S)$ **题目描述** 你有一棵 $n$ 个顶点的树 $G$ 和一个整数 $k$ 。树的顶点编号从 $1$ 到 $n$ 。 对于顶点 $r$ 和树 $G$ 的顶点的一个子集 $S$ ,使得 $|S| = k$ ,我们定义 $f(r, S)$ 为当树以 $r$ 为根时,包含 $S$ 中所有顶点的最小根子树的大小。如果一棵树的顶点集合 $T$ 是连通的,并且对于 $T$ 中的每个顶点,它的所有后裔都属于 $T$ ,则称 $T$ 为根子树。 你需要计算所有可能的顶点 $r$ 和子集 $S$ 的组合的 $f(r, S)$ 之和,其中 $|S| = k$ 。形式上,计算以下内容: $\sum_{r \in V} \sum_{S \subseteq V, |S| = k} f(r, S),$ 其中 $V$ 是树 $G$ 中的顶点集合。 输出答案对 $10^9 + 7$ 取模的结果。 **输入输出格式** **输入格式** 第一行包含两个整数 $n$ 和 $k$ ($3 \le n \le 2 \cdot 10^5$,$1 \le k \le n$)。 接下来的 $n - 1$ 行,每行包含两个整数 $x$ 和 $y$ ($1 \le x, y \le n$),表示顶点 $x$ 和 $y$ 之间的一条边。 保证给定的边构成一棵树。 **输出格式** 输出答案对 $10^9 + 7$ 取模的结果。 **输入输出样例** **输入样例 #1** ``` 3 2 1 2 1 3 ``` **输出样例 #1** ``` 25 ``` **输入样例 #2** ``` 7 2 1 2 2 3 2 4 1 5 4 6 4 7 ``` **输出样例 #2** ``` 849 ``` **说明** 第二个例子中的树如下所示:  在给定的树中,我们有 $21$ 个大小为 $2$ 的子集。因此,$S$ 属于以下集合: \{\{1, 2\}, \{1, 3\}, \{1, 4\}, \{1, 5\}, \{1, 6\}, \{1, 7\}, \{2, 3\}, \{2, 4\}, \{2, 5\}, \{2, 6\}, \{2, 7\}, \{3, 4\}, \{3, 5\}, \{3, 6\}, \{3, 7\}, \{4, 5\}, \{4, 6\}, \{4, 7\}, \{5, 6\}, \{5, 7\}, \{6, 7\}\}. 并且由于我们有 $7$ 个顶点,$1 \le r \le 7$。我们需要找到所有可能的 $r$ 和 $S$ 对的 $f(r, S)$ 之和。
**题意翻译**
给定一棵有 $n$ 个点的树,定义 $f(r,S)$ 为以 $r$ 为根时包含集合 $S$ 中所有点的最小子树的大小。
给定常数 $k$ ,对于每一对满足 $|S|=k$ 的 $S$ 和 $r$ ,求所有 $f(r,S)$ 之和,即求
$\sum_{r=1}^{n}\sum_{|S|=k}f(r,S)$
**题目描述**
你有一棵 $n$ 个顶点的树 $G$ 和一个整数 $k$ 。树的顶点编号从 $1$ 到 $n$ 。
对于顶点 $r$ 和树 $G$ 的顶点的一个子集 $S$ ,使得 $|S| = k$ ,我们定义 $f(r, S)$ 为当树以 $r$ 为根时,包含 $S$ 中所有顶点的最小根子树的大小。如果一棵树的顶点集合 $T$ 是连通的,并且对于 $T$ 中的每个顶点,它的所有后裔都属于 $T$ ,则称 $T$ 为根子树。
你需要计算所有可能的顶点 $r$ 和子集 $S$ 的组合的 $f(r, S)$ 之和,其中 $|S| = k$ 。形式上,计算以下内容:
$\sum_{r \in V} \sum_{S \subseteq V, |S| = k} f(r, S),$
其中 $V$ 是树 $G$ 中的顶点集合。
输出答案对 $10^9 + 7$ 取模的结果。
**输入输出格式**
**输入格式**
第一行包含两个整数 $n$ 和 $k$ ($3 \le n \le 2 \cdot 10^5$,$1 \le k \le n$)。
接下来的 $n - 1$ 行,每行包含两个整数 $x$ 和 $y$ ($1 \le x, y \le n$),表示顶点 $x$ 和 $y$ 之间的一条边。
保证给定的边构成一棵树。
**输出格式**
输出答案对 $10^9 + 7$ 取模的结果。
**输入输出样例**
**输入样例 #1**
```
3 2
1 2
1 3
```
**输出样例 #1**
```
25
```
**输入样例 #2**
```
7 2
1 2
2 3
2 4
1 5
4 6
4 7
```
**输出样例 #2**
```
849
```
**说明**
第二个例子中的树如下所示:

在给定的树中,我们有 $21$ 个大小为 $2$ 的子集。因此,$S$ 属于以下集合:
\{\{1, 2\}, \{1, 3\}, \{1, 4\}, \{1, 5\}, \{1, 6\}, \{1, 7\}, \{2, 3\}, \{2, 4\}, \{2, 5\}, \{2, 6\}, \{2, 7\}, \{3, 4\}, \{3, 5\}, \{3, 6\}, \{3, 7\}, \{4, 5\}, \{4, 6\}, \{4, 7\}, \{5, 6\}, \{5, 7\}, \{6, 7\}\}.
并且由于我们有 $7$ 个顶点,$1 \le r \le 7$。我们需要找到所有可能的 $r$ 和 $S$ 对的 $f(r, S)$ 之和。**K-Set Tree** **题意翻译** 给定一棵有 $n$ 个点的树,定义 $f(r,S)$ 为以 $r$ 为根时包含集合 $S$ 中所有点的最小子树的大小。 给定常数 $k$ ,对于每一对满足 $|S|=k$ 的 $S$ 和 $r$ ,求所有 $f(r,S)$ 之和,即求 $\sum_{r=1}^{n}\sum_{|S|=k}f(r,S)$ **题目描述** 你有一棵 $n$ 个顶点的树 $G$ 和一个整数 $k$ 。树的顶点编号从 $1$ 到 $n$ 。 对于顶点 $r$ 和树 $G$ 的顶点的一个子集 $S$ ,使得 $|S| = k$ ,我们定义 $f(r, S)$ 为当树以 $r$ 为根时,包含 $S$ 中所有顶点的最小根子树的大小。如果一棵树的顶点集合 $T$ 是连通的,并且对于 $T$ 中的每个顶点,它的所有后裔都属于 $T$ ,则称 $T$ 为根子树。 你需要计算所有可能的顶点 $r$ 和子集 $S$ 的组合的 $f(r, S)$ 之和,其中 $|S| = k$ 。形式上,计算以下内容: $\sum_{r \in V} \sum_{S \subseteq V, |S| = k} f(r, S),$ 其中 $V$ 是树 $G$ 中的顶点集合。 输出答案对 $10^9 + 7$ 取模的结果。 **输入输出格式** **输入格式** 第一行包含两个整数 $n$ 和 $k$ ($3 \le n \le 2 \cdot 10^5$,$1 \le k \le n$)。 接下来的 $n - 1$ 行,每行包含两个整数 $x$ 和 $y$ ($1 \le x, y \le n$),表示顶点 $x$ 和 $y$ 之间的一条边。 保证给定的边构成一棵树。 **输出格式** 输出答案对 $10^9 + 7$ 取模的结果。 **输入输出样例** **输入样例 #1** ``` 3 2 1 2 1 3 ``` **输出样例 #1** ``` 25 ``` **输入样例 #2** ``` 7 2 1 2 2 3 2 4 1 5 4 6 4 7 ``` **输出样例 #2** ``` 849 ``` **说明** 第二个例子中的树如下所示:  在给定的树中,我们有 $21$ 个大小为 $2$ 的子集。因此,$S$ 属于以下集合: \{\{1, 2\}, \{1, 3\}, \{1, 4\}, \{1, 5\}, \{1, 6\}, \{1, 7\}, \{2, 3\}, \{2, 4\}, \{2, 5\}, \{2, 6\}, \{2, 7\}, \{3, 4\}, \{3, 5\}, \{3, 6\}, \{3, 7\}, \{4, 5\}, \{4, 6\}, \{4, 7\}, \{5, 6\}, \{5, 7\}, \{6, 7\}\}. 并且由于我们有 $7$ 个顶点,$1 \le r \le 7$。我们需要找到所有可能的 $r$ 和 $S$ 对的 $f(r, S)$ 之和。