Zero Path

题意翻译

给你一个 $n \times m$ ($1 \le n, m \le 1000$) 的格点图，每个格子的值要么是 $-1$，要么是 $1$，现在问你，是否有一条从 $(1, 1)$ 到 $(n, m)$ 的路径，使得路径上经过的格点的值的和为 $0$。在路径中，只能从 $a_{i, j}$ 移动到 $a_{i + 1, j}$ 或是 $a_{i, j + 1}$（向右或是向下走）。 由 [tzyt](https://www.luogu.com.cn/user/394488) 翻译

题目描述

You are given a grid with $ n $ rows and $ m $ columns. We denote the square on the $ i $ -th ( $ 1\le i\le n $ ) row and $ j $ -th ( $ 1\le j\le m $ ) column by $ (i, j) $ and the number there by $ a_{ij} $ . All numbers are equal to $ 1 $ or to $ -1 $ . You start from the square $ (1, 1) $ and can move one square down or one square to the right at a time. In the end, you want to end up at the square $ (n, m) $ . Is it possible to move in such a way so that the sum of the values written in all the visited cells (including $ a_{11} $ and $ a_{nm} $ ) is $ 0 $ ?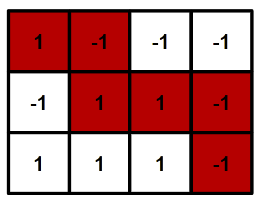 

输入输出格式

输入格式

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \leq t \leq 10^4 $ ). Description of the test cases follows. The first line of each test case contains two integers $ n $ and $ m $ ( $ 1 \le n, m \le 1000 $ ) — the size of the grid. Each of the following $ n $ lines contains $ m $ integers. The $ j $ -th integer on the $ i $ -th line is $ a_{ij} $ ( $ a_{ij} = 1 $ or $ -1 $ ) — the element in the cell $ (i, j) $ . It is guaranteed that the sum of $ n\cdot m $ over all test cases does not exceed $ 10^6 $ .

输出格式

For each test case, print "YES" if there exists a path from the top left to the bottom right that adds up to $ 0 $ , and "NO" otherwise. You can output each letter in any case.

输入输出样例

输入样例 #1

5
1 1
1
1 2
1 -1
1 4
1 -1 1 -1
3 4
1 -1 -1 -1
-1 1 1 -1
1 1 1 -1
3 4
1 -1 1 1
-1 1 -1 1
1 -1 1 1

输出样例 #1

NO
YES
YES
YES
NO

说明

One possible path for the fourth test case is given in the picture in the statement.

题意翻译

给你一个 $n \times m$ ($1 \le n, m \le 1000$) 的格点图，每个格子的值要么是 $-1$，要么是 $1$，现在问你，是否有一条从 $(1, 1)$ 到 $(n, m)$ 的路径，使得路径上经过的格点的值的和为 $0$。在路径中，只能从 $a_{i, j}$ 移动到 $a_{i + 1, j}$ 或是 $a_{i, j + 1}$（向右或是向下走）。 由 [tzyt](https://www.luogu.com.cn/user/394488) 翻译