309539: CF1695E. Ambiguous Dominoes
Memory Limit:256 MB
Time Limit:8 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Ambiguous Dominoes
题意翻译
有 $n$ 个多米诺骨牌,每张骨牌上有两个数字,要求构造两个将这 $n$ 个骨牌不重叠放入 $m\times k = 2n$ 的棋盘 $a_{m\times k}$ 中的方案,满足对应位置上的数字一样,且要求两种方案中骨牌的位置全部不一样,或报告无解。$n\le 3\times 10^5$。题目描述
Polycarp and Monocarp are both solving the same puzzle with dominoes. They are given the same set of $ n $ dominoes, the $ i $ -th of which contains two numbers $ x_i $ and $ y_i $ . They are also both given the same $ m $ by $ k $ grid of values $ a_{ij} $ such that $ m\cdot k = 2n $ . The puzzle asks them to place the $ n $ dominoes on the grid in such a way that none of them overlap, and the values on each domino match the $ a_{ij} $ values that domino covers. Dominoes can be rotated arbitrarily before being placed on the grid, so the domino $ (x_i, y_i) $ is equivalent to the domino $ (y_i, x_i) $ . They have both solved the puzzle, and compared their answers, but noticed that not only did their solutions not match, but none of the $ n $ dominoes were in the same location in both solutions! Formally, if two squares were covered by the same domino in Polycarp's solution, they were covered by different dominoes in Monocarp's solution. The diagram below shows one potential $ a $ grid, along with the two players' solutions. 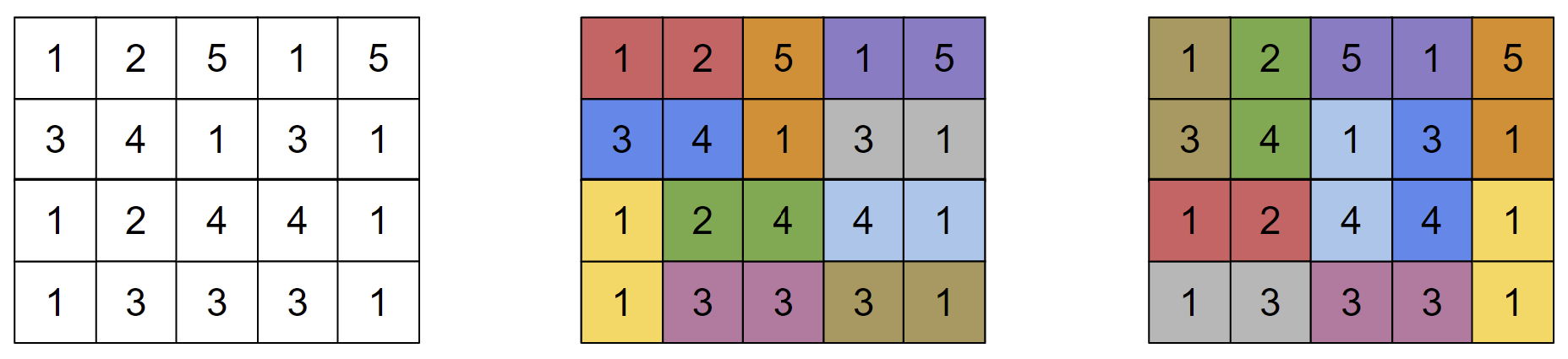Polycarp and Monocarp remember the set of dominoes they started with, but they have lost the grid $ a $ . Help them reconstruct one possible grid $ a $ , along with both of their solutions, or determine that no such grid exists.输入输出格式
输入格式
The first line contains a single integer $ n $ ( $ 1 \le n \le 3\cdot 10^5 $ ). The $ i $ -th of the next $ n $ lines contains two integers $ x_i $ and $ y_i $ ( $ 1 \le x_i, y_i \le 2n $ ).
输出格式
If there is no solution, print a single integer $ -1 $ . Otherwise, print $ m $ and $ k $ , the height and width of the puzzle grid, on the first line of output. These should satisfy $ m\cdot k = 2n $ . The $ i $ -th of the next $ m $ lines should contain $ k $ integers, the $ j $ -th of which is $ a_{ij} $ . The next $ m $ lines describe Polycarp's solution. Print $ m $ lines of $ k $ characters each. For each square, if it is covered by the upper half of a domino in Polycarp's solution, it should contain a "U". Similarly, if it is covered by the bottom, left, or right half of a domino, it should contain "D", "L", or "R", respectively. The next $ m $ lines should describe Monocarp's solution, in the same format as Polycarp's solution. If there are multiple answers, print any.
输入输出样例
输入样例 #1
1
1 2输出样例 #1
-1输入样例 #2
2
1 1
1 2输出样例 #2
2 2
2 1
1 1
LR
LR
UU
DD输入样例 #3
10
1 3
1 1
2 1
3 4
1 5
1 5
3 1
2 4
3 3
4 1输出样例 #3
4 5
1 2 5 1 5
3 4 1 3 1
1 2 4 4 1
1 3 3 3 1
LRULR
LRDLR
ULRLR
DLRLR
UULRU
DDUUD
LRDDU
LRLRD说明
Extra blank lines are added to the output for clarity, but are not required. The third sample case corresponds to the image from the statement.Input
题意翻译
有 $n$ 个多米诺骨牌,每张骨牌上有两个数字,要求构造两个将这 $n$ 个骨牌不重叠放入 $m\times k = 2n$ 的棋盘 $a_{m\times k}$ 中的方案,满足对应位置上的数字一样,且要求两种方案中骨牌的位置全部不一样,或报告无解。$n\le 3\times 10^5$。Output
**题意翻译**
给定 $n$ 个多米诺骨牌,每个骨牌上有两个数字,要求构造两种将这 $n$ 个骨牌不重叠放入 $m \times k = 2n$ 的棋盘 $a_{m \times k}$ 中的方案,满足对应位置上的数字一样,且要求两种方案中骨牌的位置全部不一样,或报告无解。$n \le 3 \times 10^5$。
**题目描述**
Polycarp 和 Monocarp 都在解决一个关于多米诺骨牌的谜题。他们被给予了相同的 $n$ 个多米诺骨牌集合,第 $i$ 个骨牌包含两个数字 $x_i$ 和 $y_i$。他们也被同时给予了一个 $m \times k$ 的值网格 $a_{ij}$,满足 $m \cdot k = 2n$。
这个谜题要求他们把 $n$ 个多米诺骨牌放置在网格上,使得它们互不重叠,并且每个多米诺骨牌上的值与其覆盖的 $a_{ij}$ 值相匹配。多米诺骨牌在放置到网格上之前可以任意旋转,所以多米诺骨牌 $(x_i, y_i)$ 与 $(y_i, x_i)$ 是等价的。
他们都已经解决了这个谜题,并比较了答案,但注意到不仅他们的解决方案不匹配,而且在两种方案中,没有一个多米诺骨牌的位置是相同的!正式地说,如果两个方格在 Polycarp 的解决方案中被同一个多米诺骨牌覆盖,那么在 Monocarp 的解决方案中,它们将被不同的多米诺骨牌覆盖。下面的图表展示了一个可能的 $a$ 网格,以及两个玩家的解决方案。

Polycarp 和 Monocarp 记得他们开始时的多米诺骨牌集合,但他们丢失了网格 $a$。帮助他们重构一个可能的网格 $a$,以及他们的解决方案,或者确定不存在这样的网格。
**输入输出格式**
**输入格式**
第一行包含一个整数 $n$ ($1 \le n \le 3 \cdot 10^5$)。
接下来 $n$ 行中的第 $i$ 行包含两个整数 $x_i$ 和 $y_i$ ($1 \le x_i, y_i \le 2n$)。
**输出格式**
如果没有解决方案,则输出一个整数 $-1$。
否则,首先输出 $m$ 和 $k$,即谜题网格的高度和宽度,满足 $m \cdot k = 2n$。
接下来的 $m$ 行中的每一行应包含 $k$ 个整数,即 $a_{ij}$。
接下来的 $m$ 行描述 Polycarp 的解决方案。对于每个方格,如果它被 Polycarp 解决方案中的多米诺骨牌的上半部分覆盖,它应包含“U”。类似地,如果它被下半部分、左半部分或右半部分覆盖,则应分别包含“D”、“L”或“R”。
接下来的 $m$ 行以与 Polycarp 解决方案相同的格式描述 Monocarp 的解决方案。
如果有多个答案,可以输出任何一个。
**输入输出样例**
**输入样例 #1**
```
1
1 2
```
**输出样例 #1**
```
-1
```
**输入样例 #2**
```
2
1 1
1 2
```
**输出样例 #2**
```
2 2
2 1
1 1
LR
LR
UU
DD
```
**输入样例 #3**
```
10
1 3
1 1
2 1
3 4
1 5
1 5
3 1
2 4
3 3
4 1
```
**输出样例 #3**
```
4 5
1 2 5 1 5
3 4 1 3 1
1 2 4 4 1
1 3 3 3 1
LRULR
LRDLR
ULRLR
DLRLR
UULRU
DDUUD
LRDDU
LRLRD
```
**说明**
为了清晰起见,输出中添加了额外的空行,但这不是必需的。
第三个示例对应于题目描述中的图像。**题意翻译** 给定 $n$ 个多米诺骨牌,每个骨牌上有两个数字,要求构造两种将这 $n$ 个骨牌不重叠放入 $m \times k = 2n$ 的棋盘 $a_{m \times k}$ 中的方案,满足对应位置上的数字一样,且要求两种方案中骨牌的位置全部不一样,或报告无解。$n \le 3 \times 10^5$。 **题目描述** Polycarp 和 Monocarp 都在解决一个关于多米诺骨牌的谜题。他们被给予了相同的 $n$ 个多米诺骨牌集合,第 $i$ 个骨牌包含两个数字 $x_i$ 和 $y_i$。他们也被同时给予了一个 $m \times k$ 的值网格 $a_{ij}$,满足 $m \cdot k = 2n$。 这个谜题要求他们把 $n$ 个多米诺骨牌放置在网格上,使得它们互不重叠,并且每个多米诺骨牌上的值与其覆盖的 $a_{ij}$ 值相匹配。多米诺骨牌在放置到网格上之前可以任意旋转,所以多米诺骨牌 $(x_i, y_i)$ 与 $(y_i, x_i)$ 是等价的。 他们都已经解决了这个谜题,并比较了答案,但注意到不仅他们的解决方案不匹配,而且在两种方案中,没有一个多米诺骨牌的位置是相同的!正式地说,如果两个方格在 Polycarp 的解决方案中被同一个多米诺骨牌覆盖,那么在 Monocarp 的解决方案中,它们将被不同的多米诺骨牌覆盖。下面的图表展示了一个可能的 $a$ 网格,以及两个玩家的解决方案。  Polycarp 和 Monocarp 记得他们开始时的多米诺骨牌集合,但他们丢失了网格 $a$。帮助他们重构一个可能的网格 $a$,以及他们的解决方案,或者确定不存在这样的网格。 **输入输出格式** **输入格式** 第一行包含一个整数 $n$ ($1 \le n \le 3 \cdot 10^5$)。 接下来 $n$ 行中的第 $i$ 行包含两个整数 $x_i$ 和 $y_i$ ($1 \le x_i, y_i \le 2n$)。 **输出格式** 如果没有解决方案,则输出一个整数 $-1$。 否则,首先输出 $m$ 和 $k$,即谜题网格的高度和宽度,满足 $m \cdot k = 2n$。 接下来的 $m$ 行中的每一行应包含 $k$ 个整数,即 $a_{ij}$。 接下来的 $m$ 行描述 Polycarp 的解决方案。对于每个方格,如果它被 Polycarp 解决方案中的多米诺骨牌的上半部分覆盖,它应包含“U”。类似地,如果它被下半部分、左半部分或右半部分覆盖,则应分别包含“D”、“L”或“R”。 接下来的 $m$ 行以与 Polycarp 解决方案相同的格式描述 Monocarp 的解决方案。 如果有多个答案,可以输出任何一个。 **输入输出样例** **输入样例 #1** ``` 1 1 2 ``` **输出样例 #1** ``` -1 ``` **输入样例 #2** ``` 2 1 1 1 2 ``` **输出样例 #2** ``` 2 2 2 1 1 1 LR LR UU DD ``` **输入样例 #3** ``` 10 1 3 1 1 2 1 3 4 1 5 1 5 3 1 2 4 3 3 4 1 ``` **输出样例 #3** ``` 4 5 1 2 5 1 5 3 4 1 3 1 1 2 4 4 1 1 3 3 3 1 LRULR LRDLR ULRLR DLRLR UULRU DDUUD LRDDU LRLRD ``` **说明** 为了清晰起见,输出中添加了额外的空行,但这不是必需的。 第三个示例对应于题目描述中的图像。
给定 $n$ 个多米诺骨牌,每个骨牌上有两个数字,要求构造两种将这 $n$ 个骨牌不重叠放入 $m \times k = 2n$ 的棋盘 $a_{m \times k}$ 中的方案,满足对应位置上的数字一样,且要求两种方案中骨牌的位置全部不一样,或报告无解。$n \le 3 \times 10^5$。
**题目描述**
Polycarp 和 Monocarp 都在解决一个关于多米诺骨牌的谜题。他们被给予了相同的 $n$ 个多米诺骨牌集合,第 $i$ 个骨牌包含两个数字 $x_i$ 和 $y_i$。他们也被同时给予了一个 $m \times k$ 的值网格 $a_{ij}$,满足 $m \cdot k = 2n$。
这个谜题要求他们把 $n$ 个多米诺骨牌放置在网格上,使得它们互不重叠,并且每个多米诺骨牌上的值与其覆盖的 $a_{ij}$ 值相匹配。多米诺骨牌在放置到网格上之前可以任意旋转,所以多米诺骨牌 $(x_i, y_i)$ 与 $(y_i, x_i)$ 是等价的。
他们都已经解决了这个谜题,并比较了答案,但注意到不仅他们的解决方案不匹配,而且在两种方案中,没有一个多米诺骨牌的位置是相同的!正式地说,如果两个方格在 Polycarp 的解决方案中被同一个多米诺骨牌覆盖,那么在 Monocarp 的解决方案中,它们将被不同的多米诺骨牌覆盖。下面的图表展示了一个可能的 $a$ 网格,以及两个玩家的解决方案。

Polycarp 和 Monocarp 记得他们开始时的多米诺骨牌集合,但他们丢失了网格 $a$。帮助他们重构一个可能的网格 $a$,以及他们的解决方案,或者确定不存在这样的网格。
**输入输出格式**
**输入格式**
第一行包含一个整数 $n$ ($1 \le n \le 3 \cdot 10^5$)。
接下来 $n$ 行中的第 $i$ 行包含两个整数 $x_i$ 和 $y_i$ ($1 \le x_i, y_i \le 2n$)。
**输出格式**
如果没有解决方案,则输出一个整数 $-1$。
否则,首先输出 $m$ 和 $k$,即谜题网格的高度和宽度,满足 $m \cdot k = 2n$。
接下来的 $m$ 行中的每一行应包含 $k$ 个整数,即 $a_{ij}$。
接下来的 $m$ 行描述 Polycarp 的解决方案。对于每个方格,如果它被 Polycarp 解决方案中的多米诺骨牌的上半部分覆盖,它应包含“U”。类似地,如果它被下半部分、左半部分或右半部分覆盖,则应分别包含“D”、“L”或“R”。
接下来的 $m$ 行以与 Polycarp 解决方案相同的格式描述 Monocarp 的解决方案。
如果有多个答案,可以输出任何一个。
**输入输出样例**
**输入样例 #1**
```
1
1 2
```
**输出样例 #1**
```
-1
```
**输入样例 #2**
```
2
1 1
1 2
```
**输出样例 #2**
```
2 2
2 1
1 1
LR
LR
UU
DD
```
**输入样例 #3**
```
10
1 3
1 1
2 1
3 4
1 5
1 5
3 1
2 4
3 3
4 1
```
**输出样例 #3**
```
4 5
1 2 5 1 5
3 4 1 3 1
1 2 4 4 1
1 3 3 3 1
LRULR
LRDLR
ULRLR
DLRLR
UULRU
DDUUD
LRDDU
LRLRD
```
**说明**
为了清晰起见,输出中添加了额外的空行,但这不是必需的。
第三个示例对应于题目描述中的图像。**题意翻译** 给定 $n$ 个多米诺骨牌,每个骨牌上有两个数字,要求构造两种将这 $n$ 个骨牌不重叠放入 $m \times k = 2n$ 的棋盘 $a_{m \times k}$ 中的方案,满足对应位置上的数字一样,且要求两种方案中骨牌的位置全部不一样,或报告无解。$n \le 3 \times 10^5$。 **题目描述** Polycarp 和 Monocarp 都在解决一个关于多米诺骨牌的谜题。他们被给予了相同的 $n$ 个多米诺骨牌集合,第 $i$ 个骨牌包含两个数字 $x_i$ 和 $y_i$。他们也被同时给予了一个 $m \times k$ 的值网格 $a_{ij}$,满足 $m \cdot k = 2n$。 这个谜题要求他们把 $n$ 个多米诺骨牌放置在网格上,使得它们互不重叠,并且每个多米诺骨牌上的值与其覆盖的 $a_{ij}$ 值相匹配。多米诺骨牌在放置到网格上之前可以任意旋转,所以多米诺骨牌 $(x_i, y_i)$ 与 $(y_i, x_i)$ 是等价的。 他们都已经解决了这个谜题,并比较了答案,但注意到不仅他们的解决方案不匹配,而且在两种方案中,没有一个多米诺骨牌的位置是相同的!正式地说,如果两个方格在 Polycarp 的解决方案中被同一个多米诺骨牌覆盖,那么在 Monocarp 的解决方案中,它们将被不同的多米诺骨牌覆盖。下面的图表展示了一个可能的 $a$ 网格,以及两个玩家的解决方案。  Polycarp 和 Monocarp 记得他们开始时的多米诺骨牌集合,但他们丢失了网格 $a$。帮助他们重构一个可能的网格 $a$,以及他们的解决方案,或者确定不存在这样的网格。 **输入输出格式** **输入格式** 第一行包含一个整数 $n$ ($1 \le n \le 3 \cdot 10^5$)。 接下来 $n$ 行中的第 $i$ 行包含两个整数 $x_i$ 和 $y_i$ ($1 \le x_i, y_i \le 2n$)。 **输出格式** 如果没有解决方案,则输出一个整数 $-1$。 否则,首先输出 $m$ 和 $k$,即谜题网格的高度和宽度,满足 $m \cdot k = 2n$。 接下来的 $m$ 行中的每一行应包含 $k$ 个整数,即 $a_{ij}$。 接下来的 $m$ 行描述 Polycarp 的解决方案。对于每个方格,如果它被 Polycarp 解决方案中的多米诺骨牌的上半部分覆盖,它应包含“U”。类似地,如果它被下半部分、左半部分或右半部分覆盖,则应分别包含“D”、“L”或“R”。 接下来的 $m$ 行以与 Polycarp 解决方案相同的格式描述 Monocarp 的解决方案。 如果有多个答案,可以输出任何一个。 **输入输出样例** **输入样例 #1** ``` 1 1 2 ``` **输出样例 #1** ``` -1 ``` **输入样例 #2** ``` 2 1 1 1 2 ``` **输出样例 #2** ``` 2 2 2 1 1 1 LR LR UU DD ``` **输入样例 #3** ``` 10 1 3 1 1 2 1 3 4 1 5 1 5 3 1 2 4 3 3 4 1 ``` **输出样例 #3** ``` 4 5 1 2 5 1 5 3 4 1 3 1 1 2 4 4 1 1 3 3 3 1 LRULR LRDLR ULRLR DLRLR UULRU DDUUD LRDDU LRLRD ``` **说明** 为了清晰起见,输出中添加了额外的空行,但这不是必需的。 第三个示例对应于题目描述中的图像。