Passable Paths (hard version)

题意翻译

给出一棵大小为 $n$ 的树，$q$ 次询问，每次给出一大小为 $m$ 的点集，判断是否存在一条链覆盖这些点，注意这条链可以经过其他点。$n,\sum m \leq 2\times 10^5$ ，$q \leq 10^5$。 翻译者：蒟蒻君HJT

题目描述

This is a hard version of the problem. The only difference between an easy and a hard version is in the number of queries. Polycarp grew a tree from $ n $ vertices. We remind you that a tree of $ n $ vertices is an undirected connected graph of $ n $ vertices and $ n-1 $ edges that does not contain cycles. He calls a set of vertices passable if there is such a path in the tree that passes through each vertex of this set without passing through any edge twice. The path can visit other vertices (not from this set). In other words, a set of vertices is called passable if there is a simple path that passes through all the vertices of this set (and possibly some other). For example, for a tree below sets $ \{3, 2, 5\} $ , $ \{1, 5, 4\} $ , $ \{1, 4\} $ are passable, and $ \{1, 3, 5\} $ , $ \{1, 2, 3, 4, 5\} $ are not. 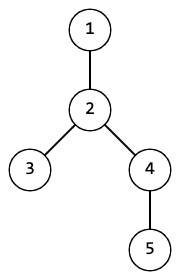Polycarp asks you to answer $ q $ queries. Each query is a set of vertices. For each query, you need to determine whether the corresponding set of vertices is passable.

输入输出格式

输入格式

The first line of input contains a single integer $ n $ ( $ 1 \le n \le 2 \cdot 10^5 $ ) — number of vertices. Following $ n - 1 $ lines a description of the tree.. Each line contains two integers $ u $ and $ v $ ( $ 1 \le u, v \le n $ , $ u \ne v $ ) — indices of vertices connected by an edge. Following line contains single integer $ q $ ( $ 1 \le q \le 10^5 $ ) — number of queries. The following $ 2 \cdot q $ lines contain descriptions of sets. The first line of the description contains an integer $ k $ ( $ 1 \le k \le n $ ) — the size of the set. The second line of the description contains $ k $ of distinct integers $ p_1, p_2, \dots, p_k $ ( $ 1 \le p_i \le n $ ) — indices of the vertices of the set. It is guaranteed that the sum of $ k $ values for all queries does not exceed $ 2 \cdot 10^5 $ .

输出格式

Output $ q $ lines, each of which contains the answer to the corresponding query. As an answer, output "YES" if the set is passable, and "NO" otherwise. You can output the answer in any case (for example, the strings "yEs", "yes", "Yes" and "YES" will be recognized as a positive answer).

输入输出样例

输入样例 #1

5
1 2
2 3
2 4
4 5
5
3
3 2 5
5
1 2 3 4 5
2
1 4
3
1 3 5
3
1 5 4

输出样例 #1

YES
NO
YES
NO
YES

输入样例 #2

5
1 2
3 2
2 4
5 2
4
2
3 1
3
3 4 5
3
2 3 5
1
1

输出样例 #2

YES
NO
YES
YES

**题目大意：**
Polycarp种了一棵有n个节点的树。我们提醒您，n个节点的树是一个有n个节点和n-1条边的无向连通图，它不包含任何的环。他称一个节点集合为可通过的，如果在这棵树中存在这样的一条路径，它恰好经过这个集合中的每个节点，且不重复经过任何一条边。这条路径可以经过其他节点（不在这个集合中）。

换句话说，如果存在一条简单路径，它恰好经过这个集合中的所有节点（也可能经过其他节点），则称这个节点集合为可通过的。

例如，对于下面的树，集合{3, 2, 5}、{1, 5, 4}、{1, 4}是可通过的，而集合{1, 3, 5}、{1, 2, 3, 4, 5}是不可通过的。

Polycarp要求您回答q个询问。每个询问都是一个节点集合。对于每个询问，您需要判断相应的节点集合是否可通过。

**输入输出数据格式：**
- **输入格式：**
- 第一行包含一个整数n（1≤n≤2×10^5）——节点数。
- 接下来n-1行描述了树的结构。
- 每行包含两个整数u和v（1≤u,v≤n，u≠v）——通过一条边相连的节点的索引。
- 下一行包含一个整数q（1≤q≤10^5）——询问数。
- 接下来2×q行包含集合的描述。
- 描述的第一行包含一个整数k（1≤k≤n）——集合的大小。
- 描述的第二行包含k个不同的整数p_1,p_2,…,p_k（1≤p_i≤n）——集合中节点的索引。
- 保证所有询问的k值之和不超过2×10^5。
- **输出格式：**
- 输出q行，每行包含对应询问的答案。如果集合是可通过的，输出"YES"，否则输出"NO"。
- 答案可以用任何形式输出（例如，字符串"yEs"、"yes"、"Yes"和"YES"都将被视为肯定答案）。**题目大意：** Polycarp种了一棵有n个节点的树。我们提醒您，n个节点的树是一个有n个节点和n-1条边的无向连通图，它不包含任何的环。他称一个节点集合为可通过的，如果在这棵树中存在这样的一条路径，它恰好经过这个集合中的每个节点，且不重复经过任何一条边。这条路径可以经过其他节点（不在这个集合中）。 换句话说，如果存在一条简单路径，它恰好经过这个集合中的所有节点（也可能经过其他节点），则称这个节点集合为可通过的。 例如，对于下面的树，集合{3, 2, 5}、{1, 5, 4}、{1, 4}是可通过的，而集合{1, 3, 5}、{1, 2, 3, 4, 5}是不可通过的。 Polycarp要求您回答q个询问。每个询问都是一个节点集合。对于每个询问，您需要判断相应的节点集合是否可通过。 **输入输出数据格式：** - **输入格式：** - 第一行包含一个整数n（1≤n≤2×10^5）——节点数。 - 接下来n-1行描述了树的结构。 - 每行包含两个整数u和v（1≤u,v≤n，u≠v）——通过一条边相连的节点的索引。 - 下一行包含一个整数q（1≤q≤10^5）——询问数。 - 接下来2×q行包含集合的描述。 - 描述的第一行包含一个整数k（1≤k≤n）——集合的大小。 - 描述的第二行包含k个不同的整数p_1,p_2,…,p_k（1≤p_i≤n）——集合中节点的索引。 - 保证所有询问的k值之和不超过2×10^5。 - **输出格式：** - 输出q行，每行包含对应询问的答案。如果集合是可通过的，输出"YES"，否则输出"NO"。 - 答案可以用任何形式输出（例如，字符串"yEs"、"yes"、"Yes"和"YES"都将被视为肯定答案）。