Qpwoeirut and Vertices

题意翻译

给出 $n$ 个点， $m$ 条边的不带权连通无向图， $q$ 次询问至少要加完编号前多少的边，才能使得 $[l,r]$ 中的所有点两两连通。 翻译者：蒟蒻君HJT

题目描述

You are given a connected undirected graph with $ n $ vertices and $ m $ edges. Vertices of the graph are numbered by integers from $ 1 $ to $ n $ and edges of the graph are numbered by integers from $ 1 $ to $ m $ . Your task is to answer $ q $ queries, each consisting of two integers $ l $ and $ r $ . The answer to each query is the smallest non-negative integer $ k $ such that the following condition holds: - For all pairs of integers $ (a, b) $ such that $ l\le a\le b\le r $ , vertices $ a $ and $ b $ are reachable from one another using only the first $ k $ edges (that is, edges $ 1, 2, \ldots, k $ ).

输入输出格式

输入格式

The first line contains a single integer $ t $ ( $ 1\le t\le 1000 $ ) — the number of test cases. The first line of each test case contains three integers $ n $ , $ m $ , and $ q $ ( $ 2\le n\le 10^5 $ , $ 1\le m, q\le 2\cdot 10^5 $ ) — the number of vertices, edges, and queries respectively. Each of the next $ m $ lines contains two integers $ u_i $ and $ v_i $ ( $ 1\le u_i, v_i\le n $ ) — ends of the $ i $ -th edge. It is guaranteed that the graph is connected and there are no multiple edges or self-loops. Each of the next $ q $ lines contains two integers $ l $ and $ r $ ( $ 1\le l\le r\le n $ ) — descriptions of the queries. It is guaranteed that that the sum of $ n $ over all test cases does not exceed $ 10^5 $ , the sum of $ m $ over all test cases does not exceed $ 2\cdot 10^5 $ , and the sum of $ q $ over all test cases does not exceed $ 2\cdot 10^5 $ .

输出格式

For each test case, print $ q $ integers — the answers to the queries.

输入输出样例

输入样例 #1

3
2 1 2
1 2
1 1
1 2
5 5 5
1 2
1 3
2 4
3 4
3 5
1 4
3 4
2 2
2 5
3 5
3 2 1
1 3
2 3
1 3

输出样例 #1

0 1 
3 3 0 5 5 
2

说明

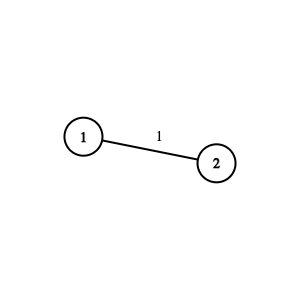Graph from the first test case. The integer near the edge is its number.In the first test case, the graph contains $ 2 $ vertices and a single edge connecting vertices $ 1 $ and $ 2 $ . In the first query, $ l=1 $ and $ r=1 $ . It is possible to reach any vertex from itself, so the answer to this query is $ 0 $ . In the second query, $ l=1 $ and $ r=2 $ . Vertices $ 1 $ and $ 2 $ are reachable from one another using only the first edge, through the path $ 1 \longleftrightarrow 2 $ . It is impossible to reach vertex $ 2 $ from vertex $ 1 $ using only the first $ 0 $ edges. So, the answer to this query is $ 1 $ . 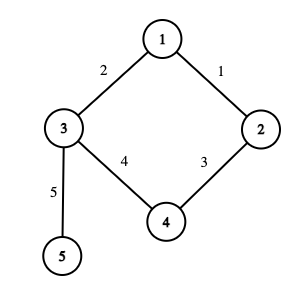Graph from the second test case. The integer near the edge is its number.In the second test case, the graph contains $ 5 $ vertices and $ 5 $ edges. In the first query, $ l=1 $ and $ r=4 $ . It is enough to use the first $ 3 $ edges to satisfy the condition from the statement: - Vertices $ 1 $ and $ 2 $ are reachable from one another through the path $ 1 \longleftrightarrow 2 $ (edge $ 1 $ ). - Vertices $ 1 $ and $ 3 $ are reachable from one another through the path $ 1 \longleftrightarrow 3 $ (edge $ 2 $ ). - Vertices $ 1 $ and $ 4 $ are reachable from one another through the path $ 1 \longleftrightarrow 2 \longleftrightarrow 4 $ (edges $ 1 $ and $ 3 $ ). - Vertices $ 2 $ and $ 3 $ are reachable from one another through the path $ 2 \longleftrightarrow 1 \longleftrightarrow 3 $ (edges $ 1 $ and $ 2 $ ). - Vertices $ 2 $ and $ 4 $ are reachable from one another through the path $ 2 \longleftrightarrow 4 $ (edge $ 3 $ ). - Vertices $ 3 $ and $ 4 $ are reachable from one another through the path $ 3 \longleftrightarrow 1 \longleftrightarrow 2 \longleftrightarrow 4 $ (edges $ 2 $ , $ 1 $ , and $ 3 $ ). If we use less than $ 3 $ of the first edges, then the condition won't be satisfied. For example, it is impossible to reach vertex $ 4 $ from vertex $ 1 $ using only the first $ 2 $ edges. So, the answer to this query is $ 3 $ . In the second query, $ l=3 $ and $ r=4 $ . Vertices $ 3 $ and $ 4 $ are reachable from one another through the path $ 3 \longleftrightarrow 1 \longleftrightarrow 2 \longleftrightarrow 4 $ (edges $ 2 $ , $ 1 $ , and $ 3 $ ). If we use any fewer of the first edges, nodes $ 3 $ and $ 4 $ will not be reachable from one another.

题意翻译

给出 $n$ 个点， $m$ 条边的不带权连通无向图， $q$ 次询问至少要加完编号前多少的边，才能使得 $[l,r]$ 中的所有点两两连通。 翻译者：蒟蒻君HJT