Empty Graph

题意翻译

给定一个长为 $n$ 的序列 $a$。 定义一个 $n$ 个点的无向完全图，点 $l$ 和点 $r$ 之间的距离为 $\min\limits_{i\in[l,r]}\{a_i\}$。 你可以进行 $k$ 次操作，每次操作可以选定 $\forall i \in [1,n]$ 并将 $a_i$ 赋值为一个 $[1,10^9]$ 的整数。请最大化这个图的直径。 设 $d(u,v)$ 表示 $u$ 到 $v$ 的最短路径长度，图的直径定义为 $\max\limits_{1\leq u < v \leq n} d(u,v)$。 输出最大化的直径长度。

题目描述

— Do you have a wish? — I want people to stop gifting each other arrays. O_o and Another Young Boy An array of $ n $ positive integers $ a_1,a_2,\ldots,a_n $ fell down on you from the skies, along with a positive integer $ k \le n $ . You can apply the following operation at most $ k $ times: - Choose an index $ 1 \le i \le n $ and an integer $ 1 \le x \le 10^9 $ . Then do $ a_i := x $ (assign $ x $ to $ a_i $ ). Then build a [complete](https://en.wikipedia.org/wiki/Complete_graph) undirected weighted graph with $ n $ vertices numbered with integers from $ 1 $ to $ n $ , where edge $ (l, r) $ ( $ 1 \le l < r \le n $ ) has weight $ \min(a_{l},a_{l+1},\ldots,a_{r}) $ . You have to find the maximum possible diameter of the resulting graph after performing at most $ k $ operations. The diameter of a graph is equal to $ \max\limits_{1 \le u < v \le n}{\operatorname{d}(u, v)} $ , where $ \operatorname{d}(u, v) $ is the length of the shortest path between vertex $ u $ and vertex $ v $ .

输入输出格式

输入格式

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10^4 $ ). Description of the test cases follows. The first line of each test case contains two integers $ n $ and $ k $ ( $ 2 \le n \le 10^5 $ , $ 1 \le k \le n $ ). The second line of each test case contains $ n $ positive integers $ a_1,a_2,\ldots,a_n $ ( $ 1 \le a_i \le 10^9 $ ). It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 10^5 $ .

输出格式

For each test case print one integer — the maximum possible diameter of the graph after performing at most $ k $ operations.

输入输出样例

输入样例 #1

6
3 1
2 4 1
3 2
1 9 84
3 1
10 2 6
3 2
179 17 1000000000
2 1
5 9
2 2
4 2

输出样例 #1

4
168
10
1000000000
9
1000000000

说明

In the first test case, one of the optimal arrays is $ [2,4,5] $ . The graph built on this array: 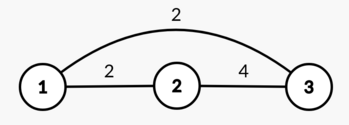 $ \operatorname{d}(1, 2) = \operatorname{d}(1, 3) = 2 $ and $ \operatorname{d}(2, 3) = 4 $ , so the diameter is equal to $ \max(2,2,4) = 4 $ .

**题目大意：**

题目定义了一个无向完全图的构建方式和图的直径。给定一个长度为 $ n $ 的序列 $ a $，图中每对点 $ l $ 和 $ r $ 之间的边权重为序列中 $ [l,r] $ 区间内元素的最小值 $ \min\limits_{i\in[l,r]}\{a_i\} $。你可以对该序列进行不超过 $ k $ 次操作，每次操作可以将序列中任意位置的数 $ a_i $ 替换为一个 $ [1,10^9] $ 范围内的整数。目标是最大化这个图的直径，即所有点对之间最短路径长度的最大值 $ \max\limits_{1\leq u < v \leq n} d(u,v) $。

**输入输出数据格式：**

**输入格式：**

- 第一行包含一个整数 $ t $，表示测试用例的数量 $ (1 \le t \le 10^4) $。
- 每个测试用例包含两行：
- 第一行包含两个整数 $ n $ 和 $ k $ $ (2 \le n \le 10^5, 1 \le k \le n) $。
- 第二行包含 $ n $ 个正整数 $ a_1, a_2, \ldots, a_n $ $ (1 \le a_i \le 10^9) $。
- 保证所有测试用例的 $ n $ 之和不超过 $ 10^5 $。

**输出格式：**

- 对于每个测试用例，输出一行，包含一个整数，表示进行不超过 $ k $ 次操作后图的最大可能直径长度。

**输入输出样例：**

**输入样例 #1:**
```
6
3 1
2 4 1
3 2
1 9 84
3 1
10 2 6
3 2
179 17 1000000000
2 1
5 9
2 2
4 2
```

**输出样例 #1:**
```
4
168
10
1000000000
9
1000000000
```

**说明：**

在第一个测试用例中，一个最优的序列是 $ [2,4,5] $。基于这个序列构建的图直径为 4。**题目大意：** 题目定义了一个无向完全图的构建方式和图的直径。给定一个长度为 $ n $ 的序列 $ a $，图中每对点 $ l $ 和 $ r $ 之间的边权重为序列中 $ [l,r] $ 区间内元素的最小值 $ \min\limits_{i\in[l,r]}\{a_i\} $。你可以对该序列进行不超过 $ k $ 次操作，每次操作可以将序列中任意位置的数 $ a_i $ 替换为一个 $ [1,10^9] $ 范围内的整数。目标是最大化这个图的直径，即所有点对之间最短路径长度的最大值 $ \max\limits_{1\leq u < v \leq n} d(u,v) $。 **输入输出数据格式：** **输入格式：** - 第一行包含一个整数 $ t $，表示测试用例的数量 $ (1 \le t \le 10^4) $。 - 每个测试用例包含两行： - 第一行包含两个整数 $ n $ 和 $ k $ $ (2 \le n \le 10^5, 1 \le k \le n) $。 - 第二行包含 $ n $ 个正整数 $ a_1, a_2, \ldots, a_n $ $ (1 \le a_i \le 10^9) $。 - 保证所有测试用例的 $ n $ 之和不超过 $ 10^5 $。 **输出格式：** - 对于每个测试用例，输出一行，包含一个整数，表示进行不超过 $ k $ 次操作后图的最大可能直径长度。 **输入输出样例：** **输入样例 #1:** ``` 6 3 1 2 4 1 3 2 1 9 84 3 1 10 2 6 3 2 179 17 1000000000 2 1 5 9 2 2 4 2 ``` **输出样例 #1:** ``` 4 168 10 1000000000 9 1000000000 ``` **说明：** 在第一个测试用例中，一个最优的序列是 $ [2,4,5] $。基于这个序列构建的图直径为 4。