309648: CF1712F. Triameter
Memory Limit:768 MB
Time Limit:4 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Triameter
题意翻译
-不是,我是说,我们的目标是什么? -去整点找直径问题。 你有一棵树,树上的每条边权值都为 $ 1 $。现在有若干次询问,每次询问一个整数 $ x $,并将叶子结点全部相连上权值为 $ x $ 的边(操作不会保留)。问每次操作后图的直径是多少。图的直径定义为 $ \underset{ 1 \leq u < v \leq n }{ \max } d(u,v) $。题目描述
— What is my mission? — To count graph diameters. You and Your Submission A tree is a connected undirected graph without cycles. A weighted tree has a weight assigned to each edge. The degree of a vertex is the number of edges connected to this vertex. You are given a weighted tree with $ n $ vertices, each edge has a weight of $ 1 $ . Let $ L $ be the set of vertices with degree equal to $ 1 $ . You have to answer $ q $ independent queries. In the $ i $ -th query: 1. You are given a positive integer $ x_i $ . 2. For all $ u,v \in L $ such that $ u < v $ , add edge $ (u, v) $ with weight $ x_i $ to the graph (initially the given tree). 3. Find the diameter of the resulting graph. The diameter of a graph is equal to $ \max\limits_{1 \le u < v \le n}{\operatorname{d}(u, v)} $ , where $ \operatorname{d}(u, v) $ is the length of the shortest path between vertex $ u $ and vertex $ v $ .输入输出格式
输入格式
The first line contains a single integer $ n $ ( $ 3 \le n \le 10^6 $ ). The second line contains $ n - 1 $ integers $ p_2,p_3,\ldots,p_n $ ( $ 1 \le p_i < i $ ) indicating that there is an edge between vertices $ i $ and $ p_i $ . It is guaranteed that the given edges form a tree. The third line contains a single integer $ q $ ( $ 1 \le q \le 10 $ ). The fourth line contains $ q $ integers $ x_1,x_2,\ldots,x_q $ ( $ 1 \le x_i \le n $ ). All $ x_i $ are distinct.
输出格式
Print $ q $ integers in a single line — the answers to the queries.
输入输出样例
输入样例 #1
4
1 2 2
4
1 2 3 4输出样例 #1
1 2 2 2输入样例 #2
7
1 2 3 4 2 1
7
2 1 3 7 5 6 4输出样例 #2
3 3 4 5 5 5 4输入样例 #3
3
1 2
1
1输出样例 #3
1说明
The graph in the first test after adding the edges: 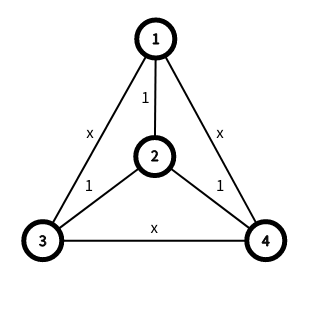Input
题意翻译
-不是,我是说,我们的目标是什么? -去整点找直径问题。 你有一棵树,树上的每条边权值都为 $ 1 $。现在有若干次询问,每次询问一个整数 $ x $,并将叶子结点全部相连上权值为 $ x $ 的边(操作不会保留)。问每次操作后图的直径是多少。图的直径定义为 $ \underset{ 1 \leq u < v \leq n }{ \max } d(u,v) $。Output
**题意翻译**
- 不是,我是说,我们的目标是什么?
- 去整点找直径问题。
- 你有一棵树,树上的每条边权值都为 $1$。现在有若干次询问,每次询问一个整数 $x$,并将叶子结点全部相连上权值为 $x$ 的边(操作不会保留)。问每次操作后图的直径是多少。图的直径定义为 $\underset{1 \leq u < v \leq n}{\max} d(u,v)$。
**题目描述**
— What is my mission?
— To count graph diameters.
You and Your Submission
A tree is a connected undirected graph without cycles. A weighted tree has a weight assigned to each edge. The degree of a vertex is the number of edges connected to this vertex.
You are given a weighted tree with $n$ vertices, each edge has a weight of $1$. Let $L$ be the set of vertices with degree equal to $1$.
You have to answer $q$ independent queries. In the $i$-th query:
1. You are given a positive integer $x_i$.
2. For all $u,v \in L$ such that $u < v$, add edge $(u, v)$ with weight $x_i$ to the graph (initially the given tree).
3. Find the diameter of the resulting graph.
The diameter of a graph is equal to $\max\limits_{1 \le u < v \le n}{\operatorname{d}(u, v)}$, where $\operatorname{d}(u, v)$ is the length of the shortest path between vertex $u$ and vertex $v$.
**输入输出格式**
**输入格式**
第一行包含一个整数 $n$ ($3 \le n \le 10^6$)。
第二行包含 $n - 1$ 个整数 $p_2,p_3,\ldots,p_n$ ($1 \le p_i < i$),表示顶点 $i$ 和 $p_i$ 之间存在一条边。保证给定的边构成一棵树。
第三行包含一个整数 $q$ ($1 \le q \le 10$)。
第四行包含 $q$ 个整数 $x_1,x_2,\ldots,x_q$ ($1 \le x_i \le n$)。所有 $x_i$ 都是不相同的。
**输出格式**
打印一行 $q$ 个整数——对查询的答案。
**输入输出样例**
**输入样例 #1**
```
4
1 2 2
4
1 2 3 4
```
**输出样例 #1**
```
1 2 2 2
```
**输入样例 #2**
```
7
1 2 3 4 2 1
7
2 1 3 7 5 6 4
```
**输出样例 #2**
```
3 3 4 5 5 5 4
```
**输入样例 #3**
```
3
1 2
1
1
```
**输出样例 #3**
```
1
```
**说明**
第一个测试用例在添加边之后的图如下:
**题意翻译** - 不是,我是说,我们的目标是什么? - 去整点找直径问题。 - 你有一棵树,树上的每条边权值都为 $1$。现在有若干次询问,每次询问一个整数 $x$,并将叶子结点全部相连上权值为 $x$ 的边(操作不会保留)。问每次操作后图的直径是多少。图的直径定义为 $\underset{1 \leq u < v \leq n}{\max} d(u,v)$。 **题目描述** — What is my mission? — To count graph diameters. You and Your Submission A tree is a connected undirected graph without cycles. A weighted tree has a weight assigned to each edge. The degree of a vertex is the number of edges connected to this vertex. You are given a weighted tree with $n$ vertices, each edge has a weight of $1$. Let $L$ be the set of vertices with degree equal to $1$. You have to answer $q$ independent queries. In the $i$-th query: 1. You are given a positive integer $x_i$. 2. For all $u,v \in L$ such that $u < v$, add edge $(u, v)$ with weight $x_i$ to the graph (initially the given tree). 3. Find the diameter of the resulting graph. The diameter of a graph is equal to $\max\limits_{1 \le u < v \le n}{\operatorname{d}(u, v)}$, where $\operatorname{d}(u, v)$ is the length of the shortest path between vertex $u$ and vertex $v$. **输入输出格式** **输入格式** 第一行包含一个整数 $n$ ($3 \le n \le 10^6$)。 第二行包含 $n - 1$ 个整数 $p_2,p_3,\ldots,p_n$ ($1 \le p_i < i$),表示顶点 $i$ 和 $p_i$ 之间存在一条边。保证给定的边构成一棵树。 第三行包含一个整数 $q$ ($1 \le q \le 10$)。 第四行包含 $q$ 个整数 $x_1,x_2,\ldots,x_q$ ($1 \le x_i \le n$)。所有 $x_i$ 都是不相同的。 **输出格式** 打印一行 $q$ 个整数——对查询的答案。 **输入输出样例** **输入样例 #1** ``` 4 1 2 2 4 1 2 3 4 ``` **输出样例 #1** ``` 1 2 2 2 ``` **输入样例 #2** ``` 7 1 2 3 4 2 1 7 2 1 3 7 5 6 4 ``` **输出样例 #2** ``` 3 3 4 5 5 5 4 ``` **输入样例 #3** ``` 3 1 2 1 1 ``` **输出样例 #3** ``` 1 ``` **说明** 第一个测试用例在添加边之后的图如下: 
- 不是,我是说,我们的目标是什么?
- 去整点找直径问题。
- 你有一棵树,树上的每条边权值都为 $1$。现在有若干次询问,每次询问一个整数 $x$,并将叶子结点全部相连上权值为 $x$ 的边(操作不会保留)。问每次操作后图的直径是多少。图的直径定义为 $\underset{1 \leq u < v \leq n}{\max} d(u,v)$。
**题目描述**
— What is my mission?
— To count graph diameters.
You and Your Submission
A tree is a connected undirected graph without cycles. A weighted tree has a weight assigned to each edge. The degree of a vertex is the number of edges connected to this vertex.
You are given a weighted tree with $n$ vertices, each edge has a weight of $1$. Let $L$ be the set of vertices with degree equal to $1$.
You have to answer $q$ independent queries. In the $i$-th query:
1. You are given a positive integer $x_i$.
2. For all $u,v \in L$ such that $u < v$, add edge $(u, v)$ with weight $x_i$ to the graph (initially the given tree).
3. Find the diameter of the resulting graph.
The diameter of a graph is equal to $\max\limits_{1 \le u < v \le n}{\operatorname{d}(u, v)}$, where $\operatorname{d}(u, v)$ is the length of the shortest path between vertex $u$ and vertex $v$.
**输入输出格式**
**输入格式**
第一行包含一个整数 $n$ ($3 \le n \le 10^6$)。
第二行包含 $n - 1$ 个整数 $p_2,p_3,\ldots,p_n$ ($1 \le p_i < i$),表示顶点 $i$ 和 $p_i$ 之间存在一条边。保证给定的边构成一棵树。
第三行包含一个整数 $q$ ($1 \le q \le 10$)。
第四行包含 $q$ 个整数 $x_1,x_2,\ldots,x_q$ ($1 \le x_i \le n$)。所有 $x_i$ 都是不相同的。
**输出格式**
打印一行 $q$ 个整数——对查询的答案。
**输入输出样例**
**输入样例 #1**
```
4
1 2 2
4
1 2 3 4
```
**输出样例 #1**
```
1 2 2 2
```
**输入样例 #2**
```
7
1 2 3 4 2 1
7
2 1 3 7 5 6 4
```
**输出样例 #2**
```
3 3 4 5 5 5 4
```
**输入样例 #3**
```
3
1 2
1
1
```
**输出样例 #3**
```
1
```
**说明**
第一个测试用例在添加边之后的图如下:
**题意翻译** - 不是,我是说,我们的目标是什么? - 去整点找直径问题。 - 你有一棵树,树上的每条边权值都为 $1$。现在有若干次询问,每次询问一个整数 $x$,并将叶子结点全部相连上权值为 $x$ 的边(操作不会保留)。问每次操作后图的直径是多少。图的直径定义为 $\underset{1 \leq u < v \leq n}{\max} d(u,v)$。 **题目描述** — What is my mission? — To count graph diameters. You and Your Submission A tree is a connected undirected graph without cycles. A weighted tree has a weight assigned to each edge. The degree of a vertex is the number of edges connected to this vertex. You are given a weighted tree with $n$ vertices, each edge has a weight of $1$. Let $L$ be the set of vertices with degree equal to $1$. You have to answer $q$ independent queries. In the $i$-th query: 1. You are given a positive integer $x_i$. 2. For all $u,v \in L$ such that $u < v$, add edge $(u, v)$ with weight $x_i$ to the graph (initially the given tree). 3. Find the diameter of the resulting graph. The diameter of a graph is equal to $\max\limits_{1 \le u < v \le n}{\operatorname{d}(u, v)}$, where $\operatorname{d}(u, v)$ is the length of the shortest path between vertex $u$ and vertex $v$. **输入输出格式** **输入格式** 第一行包含一个整数 $n$ ($3 \le n \le 10^6$)。 第二行包含 $n - 1$ 个整数 $p_2,p_3,\ldots,p_n$ ($1 \le p_i < i$),表示顶点 $i$ 和 $p_i$ 之间存在一条边。保证给定的边构成一棵树。 第三行包含一个整数 $q$ ($1 \le q \le 10$)。 第四行包含 $q$ 个整数 $x_1,x_2,\ldots,x_q$ ($1 \le x_i \le n$)。所有 $x_i$ 都是不相同的。 **输出格式** 打印一行 $q$ 个整数——对查询的答案。 **输入输出样例** **输入样例 #1** ``` 4 1 2 2 4 1 2 3 4 ``` **输出样例 #1** ``` 1 2 2 2 ``` **输入样例 #2** ``` 7 1 2 3 4 2 1 7 2 1 3 7 5 6 4 ``` **输出样例 #2** ``` 3 3 4 5 5 5 4 ``` **输入样例 #3** ``` 3 1 2 1 1 ``` **输出样例 #3** ``` 1 ``` **说明** 第一个测试用例在添加边之后的图如下: 