309653: CF1713E. Cross Swapping
Memory Limit:256 MB
Time Limit:1 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Cross Swapping
题意翻译
给定一个 $n\times n$ 的矩阵。一次操作可以给定一个 $k$ 然后交换所有的 $A_{i,k}$ 和 $A_{k,i}$ 。 如图表示 $n=4,k=3$ 的情况。 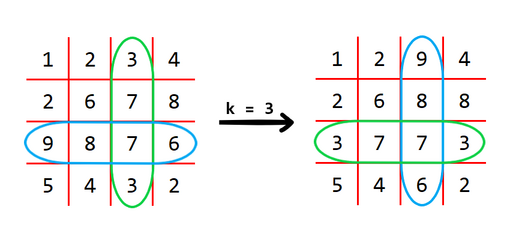 求若干次操作后字典序最小的矩阵。题目描述
You are given a square matrix $ A $ of size $ n \times n $ whose elements are integers. We will denote the element on the intersection of the $ i $ -th row and the $ j $ -th column as $ A_{i,j} $ . You can perform operations on the matrix. In each operation, you can choose an integer $ k $ , then for each index $ i $ ( $ 1 \leq i \leq n $ ), swap $ A_{i, k} $ with $ A_{k, i} $ . Note that cell $ A_{k, k} $ remains unchanged. For example, for $ n = 4 $ and $ k = 3 $ , this matrix will be transformed like this: The operation $ k = 3 $ swaps the blue row with the green column.You can perform this operation any number of times. Find the lexicographically smallest matrix $ ^\dagger $ you can obtain after performing arbitrary number of operations. $ {}^\dagger $ For two matrices $ A $ and $ B $ of size $ n \times n $ , let $ a_{(i-1) \cdot n + j} = A_{i,j} $ and $ b_{(i-1) \cdot n + j} = B_{i,j} $ . Then, the matrix $ A $ is lexicographically smaller than the matrix $ B $ when there exists an index $ i $ ( $ 1 \leq i \leq n^2 $ ) such that $ a_i < b_i $ and for all indices $ j $ such that $ 1 \leq j < i $ , $ a_j = b_j $ .输入输出格式
输入格式
The first line contains a single integer $ t $ ( $ 1 \leq t \leq 10^5 $ ) — the number of test cases. The first line of each test case contains a single integer $ n $ ( $ 1 \leq n \leq 1000 $ ) — the size of the matrix. The $ i $ -th line of the next $ n $ lines contains $ n $ integers $ A_{i, 1}, A_{i, 2}, \dots, A_{i, n} $ ( $ 1 \le A_{i, j} \le 10^9 $ ) — description of the matrix $ A $ . It is guaranteed that the sum of $ n^2 $ over all test cases does not exceed $ 10^6 $ .
输出格式
For each test case, print $ n $ lines with $ n $ integers each — the lexicographically smallest matrix.
输入输出样例
输入样例 #1
2
3
2 1 2
2 1 2
1 1 2
4
3 3 1 2
1 1 3 1
3 2 3 2
2 3 3 1输出样例 #1
2 1 1
2 1 1
2 2 2
3 1 1 2
3 1 2 1
3 3 3 3
2 3 2 1说明
Note that in every picture below the matrix is transformed in such a way that the blue rows are swapped with the green columns. In the first test case, we can perform $ 1 $ operation for $ k = 3 $ . The matrix will be transformed as below: 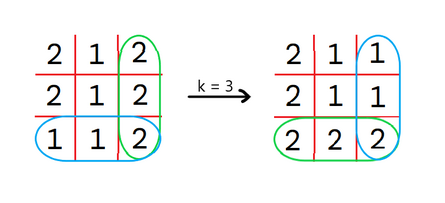 In the second test case, we can perform $ 2 $ operations for $ k = 1 $ and $ k = 3 $ : 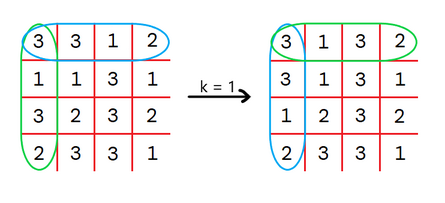 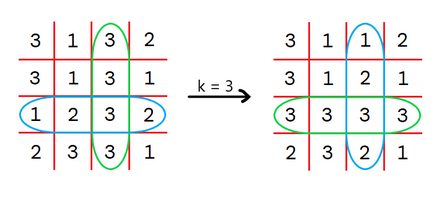Input
题意翻译
给定一个 $n\times n$ 的矩阵。一次操作可以给定一个 $k$ 然后交换所有的 $A_{i,k}$ 和 $A_{k,i}$ 。 如图表示 $n=4,k=3$ 的情况。  求若干次操作后字典序最小的矩阵。Output
题目大意:
给定一个n×n的矩阵。可以选择一个整数k,然后交换所有的A_{i,k}和A_{k,i}。
求若干次操作后字典序最小的矩阵。
输入输出数据格式:
输入格式:
第一行包含一个整数t(1≤t≤10^5)——测试用例的数量。
每个测试用例的第一行包含一个整数n(1≤n≤1000)——矩阵的大小。
接下来的n行,每行包含n个整数A_{i,1},A_{i,2},…,A_{i,n}(1≤A_{i,j}≤10^9)——矩阵A的描述。
保证所有测试用例的n^2之和不超过10^6。
输出格式:
对于每个测试用例,输出n行,每行n个整数——字典序最小的矩阵。题目大意: 给定一个n×n的矩阵。可以选择一个整数k,然后交换所有的A_{i,k}和A_{k,i}。 求若干次操作后字典序最小的矩阵。 输入输出数据格式: 输入格式: 第一行包含一个整数t(1≤t≤10^5)——测试用例的数量。 每个测试用例的第一行包含一个整数n(1≤n≤1000)——矩阵的大小。 接下来的n行,每行包含n个整数A_{i,1},A_{i,2},…,A_{i,n}(1≤A_{i,j}≤10^9)——矩阵A的描述。 保证所有测试用例的n^2之和不超过10^6。 输出格式: 对于每个测试用例,输出n行,每行n个整数——字典序最小的矩阵。
给定一个n×n的矩阵。可以选择一个整数k,然后交换所有的A_{i,k}和A_{k,i}。
求若干次操作后字典序最小的矩阵。
输入输出数据格式:
输入格式:
第一行包含一个整数t(1≤t≤10^5)——测试用例的数量。
每个测试用例的第一行包含一个整数n(1≤n≤1000)——矩阵的大小。
接下来的n行,每行包含n个整数A_{i,1},A_{i,2},…,A_{i,n}(1≤A_{i,j}≤10^9)——矩阵A的描述。
保证所有测试用例的n^2之和不超过10^6。
输出格式:
对于每个测试用例,输出n行,每行n个整数——字典序最小的矩阵。题目大意: 给定一个n×n的矩阵。可以选择一个整数k,然后交换所有的A_{i,k}和A_{k,i}。 求若干次操作后字典序最小的矩阵。 输入输出数据格式: 输入格式: 第一行包含一个整数t(1≤t≤10^5)——测试用例的数量。 每个测试用例的第一行包含一个整数n(1≤n≤1000)——矩阵的大小。 接下来的n行,每行包含n个整数A_{i,1},A_{i,2},…,A_{i,n}(1≤A_{i,j}≤10^9)——矩阵A的描述。 保证所有测试用例的n^2之和不超过10^6。 输出格式: 对于每个测试用例,输出n行,每行n个整数——字典序最小的矩阵。