Crossmarket

题意翻译

### 题意翻译 有一个 $n \times m$ 的空间， Stanley 需要从左上角到右下角； Megan 则需要从左下角到右上角。 两人可以耗费 $1$ 能量到达相邻的格子。 同时为了加快到达的速度， Megan 会在经过的所有格子留下传送门，两人可以耗费 $1$ 能量通过任意传送门通往任意有传送门的位置。 求两人均到达目的地耗费的最小总能量。 by SenGYi

题目描述

Stanley and Megan decided to shop in the "Crossmarket" grocery store, which can be represented as a matrix with $ n $ rows and $ m $ columns. Stanley and Megan can move to an adjacent cell using $ 1 $ unit of power. Two cells are considered adjacent if they share an edge. To speed up the shopping process, Megan brought her portals with her, and she leaves one in each cell she visits (if there is no portal yet). If a person (Stanley or Megan) is in a cell with a portal, that person can use $ 1 $ unit of power to teleport to any other cell with a portal, including Megan's starting cell. They decided to split up: Stanley will go from the upper-left cell (cell with coordinates $ (1, 1) $ ) to the lower-right cell (cell with coordinates $ (n, m) $ ), whilst Megan needs to get from the lower-left cell (cell with coordinates $ (n, 1) $ ) to the upper-right cell (cell with coordinates $ (1, m) $ ). What is the minimum total energy needed for them both to do that? Note that they can choose the time they move. Time does not affect energy.

输入输出格式

输入格式

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 1000 $ ). Description of the test cases follows. The only line in the test case contains two integers $ n $ and $ m $ ( $ 1 \le n, m \le 10^5 $ ).

输出格式

For each test case print a single integer on a new line – the answer.

输入输出样例

输入样例 #1

7
7 5
5 7
1 1
100000 100000
57 228
1 5
5 1

输出样例 #1

15
15
0
299998
340
5
5

说明

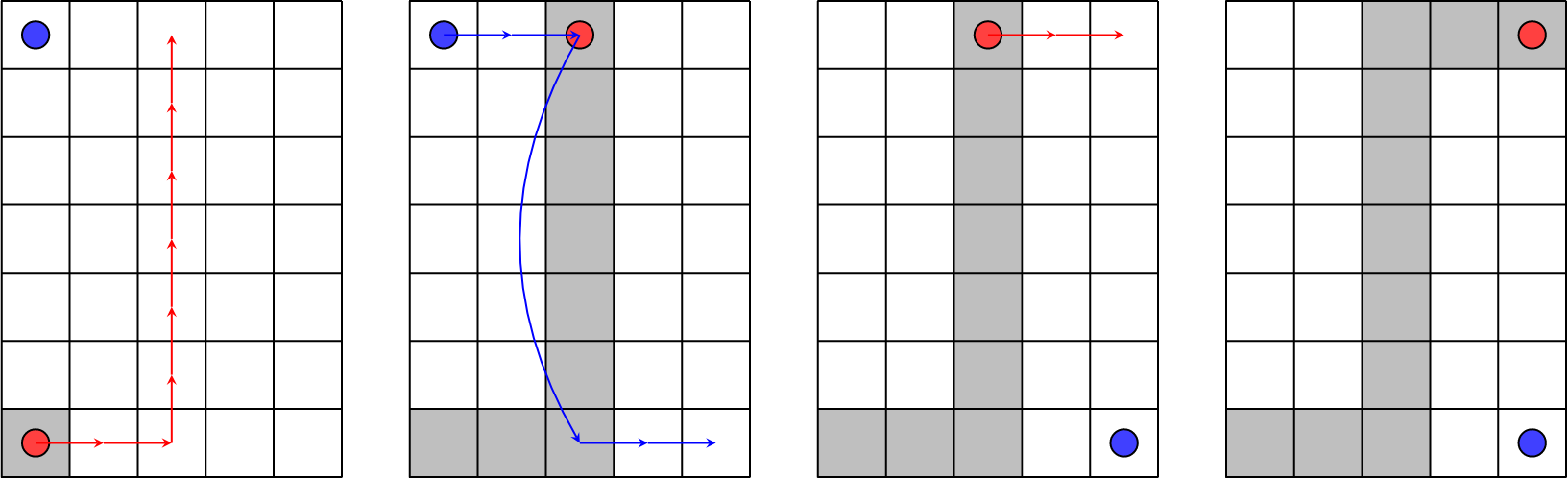In the first test case they can stick to the following plan: 1. Megan (red circle) moves to the cell $ (7, 3) $ . Then she goes to the cell $ (1, 3) $ , and Stanley (blue circle) does the same. 2. Stanley uses the portal in that cell (cells with portals are grey) to get to the cell $ (7, 3) $ . Then he moves to his destination — cell $ (7, 5) $ . 3. Megan also finishes her route and goes to the cell $ (1, 5) $ . The total energy spent is $ (2 + 6) + (2 + 1 + 2) + (2)= 15 $ , which is our final answer.

题目大意：
有一个 n×m 的网格，Stanley 需要从左上角走到右下角；Megan 需要从左下角走到右上角。他们每移动到一个相邻的格子需要耗费 1 点能量。Megan 可以在每个经过的格子留下传送门，通过传送门到达任意有传送门的位置也需要耗费 1 点能量。求两人到达目的地所需的最小总能量。

输入输出格式：
输入格式：第一行包含一个整数 t (1≤t≤1000)，表示测试用例的数量。接下来 t 行，每行包含两个整数 n 和 m (1≤n,m≤10^5)，表示网格的行数和列数。
输出格式：对于每个测试用例，输出一行，包含一个整数，表示两人到达目的地所需的最小总能量。

输入输出样例：
输入样例 #1：
```
7
7 5
5 7
1 1
100000 100000
57 228
1 5
5 1
```
输出样例 #1：
```
15
15
0
299998
340
5
5
```
题目大意： 有一个 n×m 的网格，Stanley 需要从左上角走到右下角；Megan 需要从左下角走到右上角。他们每移动到一个相邻的格子需要耗费 1 点能量。Megan 可以在每个经过的格子留下传送门，通过传送门到达任意有传送门的位置也需要耗费 1 点能量。求两人到达目的地所需的最小总能量。 输入输出格式： 输入格式：第一行包含一个整数 t (1≤t≤1000)，表示测试用例的数量。接下来 t 行，每行包含两个整数 n 和 m (1≤n,m≤10^5)，表示网格的行数和列数。 输出格式：对于每个测试用例，输出一行，包含一个整数，表示两人到达目的地所需的最小总能量。 输入输出样例： 输入样例 #1： ``` 7 7 5 5 7 1 1 100000 100000 57 228 1 5 5 1 ``` 输出样例 #1： ``` 15 15 0 299998 340 5 5 ```