Counting Rectangles

题意翻译

分别给定 $n$ 个正整数 $h_i,w_i$ ，有 $q$ 次询问。 对于每次询问，输入四个整数 $h_s,w_s,h_b,w_b$，输出满足 $h_i \in (h_s,h_b)$ ,$w_i\in(w_s,w_b)$ 的 $\sum h_i \cdot w_i$

题目描述

You have $ n $ rectangles, the $ i $ -th rectangle has height $ h_i $ and width $ w_i $ . You are asked $ q $ queries of the form $ h_s \ w_s \ h_b \ w_b $ . For each query output, the total area of rectangles you own that can fit a rectangle of height $ h_s $ and width $ w_s $ while also fitting in a rectangle of height $ h_b $ and width $ w_b $ . In other words, print $ \sum h_i \cdot w_i $ for $ i $ such that $ h_s < h_i < h_b $ and $ w_s < w_i < w_b $ . Please note, that if two rectangles have the same height or the same width, then they cannot fit inside each other. Also note that you cannot rotate rectangles. Please note that the answer for some test cases won't fit into 32-bit integer type, so you should use at least 64-bit integer type in your programming language (like long long for C++).

输入输出格式

输入格式

The first line of the input contains an integer $ t $ ( $ 1 \leq t \leq 100 $ ) — the number of test cases. The first line of each test case two integers $ n, q $ ( $ 1 \leq n \leq 10^5 $ ; $ 1 \leq q \leq 10^5 $ ) — the number of rectangles you own and the number of queries. Then $ n $ lines follow, each containing two integers $ h_i, w_i $ ( $ 1 \leq h_i, w_i \leq 1000 $ ) — the height and width of the $ i $ -th rectangle. Then $ q $ lines follow, each containing four integers $ h_s, w_s, h_b, w_b $ ( $ 1 \leq h_s < h_b,\ w_s < w_b \leq 1000 $ ) — the description of each query. The sum of $ q $ over all test cases does not exceed $ 10^5 $ , and the sum of $ n $ over all test cases does not exceed $ 10^5 $ .

输出格式

For each test case, output $ q $ lines, the $ i $ -th line containing the answer to the $ i $ -th query.

输入输出样例

输入样例 #1

3
2 1
2 3
3 2
1 1 3 4
5 5
1 1
2 2
3 3
4 4
5 5
3 3 6 6
2 1 4 5
1 1 2 10
1 1 100 100
1 1 3 3
3 1
999 999
999 999
999 998
1 1 1000 1000

输出样例 #1

6
41
9
0
54
4
2993004

说明

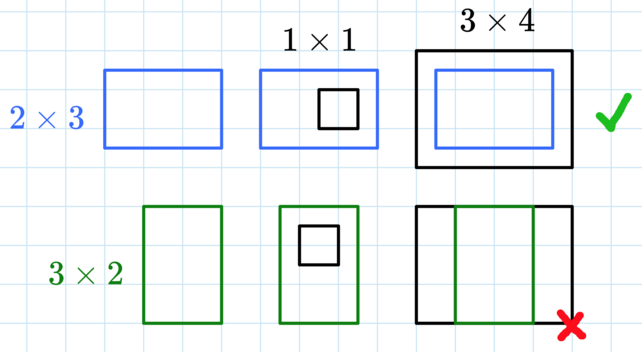In the first test case, there is only one query. We need to find the sum of areas of all rectangles that can fit a $ 1 \times 1 $ rectangle inside of it and fit into a $ 3 \times 4 $ rectangle. Only the $ 2 \times 3 $ rectangle works, because $ 1 < 2 $ (comparing heights) and $ 1 < 3 $ (comparing widths), so the $ 1 \times 1 $ rectangle fits inside, and $ 2 < 3 $ (comparing heights) and $ 3 < 4 $ (comparing widths), so it fits inside the $ 3 \times 4 $ rectangle. The $ 3 \times 2 $ rectangle is too tall to fit in a $ 3 \times 4 $ rectangle. The total area is $ 2 \cdot 3 = 6 $ .

**题目大意**：

给定 $n$ 个矩形，每个矩形的高度为 $h_i$ 和宽度为 $w_i$。进行 $q$ 次询问，每次询问包含四个整数 $h_s, w_s, h_b, w_b$。对于每次询问，输出所有高度在 $h_s$ 和 $h_b$ 之间且宽度在 $w_s$ 和 $w_b$ 之间的矩形的面积之和，即满足 $h_s < h_i < h_b$ 和 $w_s < w_i < w_b$ 的 $\sum h_i \cdot w_i$。注意，如果有两个矩形的高度或宽度相同，那么它们不能相互嵌套。不能旋转矩形。注意，某些测试用例的答案可能不适合 32 位整数类型，因此您应该在编程语言中使用至少 64 位整数类型（例如 C++ 中的 long long）。

**输入输出格式**：

**输入格式**：

第一行包含一个整数 $t$（$1 \leq t \leq 100$）——测试用例的数量。

每个测试用例的第一行包含两个整数 $n, q$（$1 \leq n \leq 10^5$；$1 \leq q \leq 10^5$）——你拥有的矩形数量和查询数量。

然后是 $n$ 行，每行包含两个整数 $h_i, w_i$（$1 \leq h_i, w_i \leq 1000$）——第 $i$ 个矩形的高度和宽度。

然后是 $q$ 行，每行包含四个整数 $h_s, w_s, h_b, w_b$（$1 \leq h_s < h_b, w_s < w_b \leq 1000$）——每个查询的描述。

所有测试用例的 $q$ 之和不超过 $10^5$，所有测试用例的 $n$ 之和不超过 $10^5$。

**输出格式**：

对于每个测试用例，输出 $q$ 行，第 $i$ 行包含对第 $i$ 个查询的答案。

**输入输出样例**：

**输入样例 #1**:

```
3
2 1
2 3
3 2
1 1 3 4
5 5
1 1
2 2
3 3
4 4
5 5
3 3 6 6
2 1 4 5
1 1 2 10
1 1 100 100
1 1 3 3
3 1
999 999
999 999
999 998
1 1 1000 1000
```

**输出样例 #1**:

```
6
41
9
0
54
4
2993004
```

**说明**：

在第一个测试用例中，只有一个查询。我们需要找到所有可以容纳 $1 \times 1$ 矩形且能放入 $3 \times 4$ 矩形内的矩形的面积之和。

只有 $2 \times 3$ 矩形符合条件，因为 $1 < 2$（比较高度）和 $1 < 3$（比较宽度），所以 $1 \times 1$ 矩形可以放入其中，且 $2 < 3$（比较高度）和 $3 < 4$（比较宽度），所以它可以放入 $3 \times 4$ 矩形内。$3 \times 2$ 矩形太高，无法放入 $3 \times 4$ 矩形中。总面积为 $2 \cdot 3 = 6$。**题目大意**： 给定 $n$ 个矩形，每个矩形的高度为 $h_i$ 和宽度为 $w_i$。进行 $q$ 次询问，每次询问包含四个整数 $h_s, w_s, h_b, w_b$。对于每次询问，输出所有高度在 $h_s$ 和 $h_b$ 之间且宽度在 $w_s$ 和 $w_b$ 之间的矩形的面积之和，即满足 $h_s < h_i < h_b$ 和 $w_s < w_i < w_b$ 的 $\sum h_i \cdot w_i$。注意，如果有两个矩形的高度或宽度相同，那么它们不能相互嵌套。不能旋转矩形。注意，某些测试用例的答案可能不适合 32 位整数类型，因此您应该在编程语言中使用至少 64 位整数类型（例如 C++ 中的 long long）。 **输入输出格式**： **输入格式**： 第一行包含一个整数 $t$（$1 \leq t \leq 100$）——测试用例的数量。 每个测试用例的第一行包含两个整数 $n, q$（$1 \leq n \leq 10^5$；$1 \leq q \leq 10^5$）——你拥有的矩形数量和查询数量。 然后是 $n$ 行，每行包含两个整数 $h_i, w_i$（$1 \leq h_i, w_i \leq 1000$）——第 $i$ 个矩形的高度和宽度。 然后是 $q$ 行，每行包含四个整数 $h_s, w_s, h_b, w_b$（$1 \leq h_s < h_b, w_s < w_b \leq 1000$）——每个查询的描述。 所有测试用例的 $q$ 之和不超过 $10^5$，所有测试用例的 $n$ 之和不超过 $10^5$。 **输出格式**： 对于每个测试用例，输出 $q$ 行，第 $i$ 行包含对第 $i$ 个查询的答案。 **输入输出样例**： **输入样例 #1**: ``` 3 2 1 2 3 3 2 1 1 3 4 5 5 1 1 2 2 3 3 4 4 5 5 3 3 6 6 2 1 4 5 1 1 2 10 1 1 100 100 1 1 3 3 3 1 999 999 999 999 999 998 1 1 1000 1000 ``` **输出样例 #1**: ``` 6 41 9 0 54 4 2993004 ``` **说明**： 在第一个测试用例中，只有一个查询。我们需要找到所有可以容纳 $1 \times 1$ 矩形且能放入 $3 \times 4$ 矩形内的矩形的面积之和。 只有 $2 \times 3$ 矩形符合条件，因为 $1 < 2$（比较高度）和 $1 < 3$（比较宽度），所以 $1 \times 1$ 矩形可以放入其中，且 $2 < 3$（比较高度）和 $3 < 4$（比较宽度），所以它可以放入 $3 \times 4$ 矩形内。$3 \times 2$ 矩形太高，无法放入 $3 \times 4$ 矩形中。总面积为 $2 \cdot 3 = 6$。