Moving Both Hands

题意翻译

**题目描述** Alice 在进行一个有向图上做游戏。有向图上共有 $n$ 个节点，$m$ 条有向边。Alice的手上有 一个红色球和一个蓝色球。 游戏开始时，Alice将红色球放在 $1$ 号节点上，将蓝色球放在 $i$ 号节点上。 长度为 $w$ 的有向边表示可以通过一次操作将在 $v$ 的点转移 到 $u$ 花费 $w$时间。 每局游戏中，Alice 要通过尽可能少的时间将两个球共同转移到任意同一个节点上。Alice 同一时间只能操作一个球。现在 Alice 想知道对于每个点 $2\le i \le n$ ，每局游戏完成的最小时间是 多少。 **输入格式** 输入第一行是两个整数 $n$ ，$m$。 接下来 $m$行，每行三个整数 $u$，$v$，$w$，表示图上有一条从 $u$ 指向 $v$ 长为 $w$ 的有向边。 **输出格式** 输出 $n$ 行，每行一个整数，第 $i$ 行的整数表示蓝色球开始时在 $i$ 号点上时游戏的 最小完成时间。如果不能完成游戏，输出 -1 。

题目描述

Pak Chanek is playing one of his favourite board games. In the game, there is a directed graph with $ N $ vertices and $ M $ edges. In the graph, edge $ i $ connects two different vertices $ U_i $ and $ V_i $ with a length of $ W_i $ . By using the $ i $ -th edge, something can move from $ U_i $ to $ V_i $ , but not from $ V_i $ to $ U_i $ . To play this game, initially Pak Chanek must place both of his hands onto two different vertices. In one move, he can move one of his hands to another vertex using an edge. To move a hand from vertex $ U_i $ to vertex $ V_i $ , Pak Chanek needs a time of $ W_i $ seconds. Note that Pak Chanek can only move one hand at a time. This game ends when both of Pak Chanek's hands are on the same vertex. Pak Chanek has several questions. For each $ p $ satisfying $ 2 \leq p \leq N $ , you need to find the minimum time in seconds needed for Pak Chanek to end the game if initially Pak Chanek's left hand and right hand are placed on vertex $ 1 $ and vertex $ p $ , or report if it is impossible.

输入输出格式

输入格式

The first line contains two integers $ N $ and $ M $ ( $ 2 \leq N \leq 10^5 $ , $ 0 \leq M \leq 2 \cdot 10^5 $ ) — the number of vertices and edges in the graph. The $ i $ -th of the next $ M $ lines contains three integers $ U_i $ , $ V_i $ , and $ W_i $ ( $ 1 \le U_i, V_i \le N $ , $ U_i \neq V_i $ , $ 1 \le W_i \le 10^9 $ ) — a directed edge that connects two different vertices $ U_i $ and $ V_i $ with a length of $ W_i $ . There is no pair of different edges $ i $ and $ j $ such that $ U_i = U_j $ and $ V_i = V_j $ .

输出格式

Output a line containing $ N-1 $ integers. The $ j $ -th integer represents the minimum time in seconds needed by Pak Chanek to end the game if initially Pak Chanek's left hand and right hand are placed on vertex $ 1 $ and vertex $ j+1 $ , or $ -1 $ if it is impossible.

输入输出样例

输入样例 #1

5 7
1 2 2
2 4 1
4 1 4
2 5 3
5 4 1
5 2 4
2 1 1

输出样例 #1

1 -1 3 4

说明

If initially Pak Chanek's left hand is on vertex $ 1 $ and his right hand is on vertex $ 5 $ , Pak Chanek can do the following moves: 1. Move his right hand to vertex $ 4 $ in $ 1 $ second. 2. Move his left hand to vertex $ 2 $ in $ 2 $ seconds. 3. Move his left hand to vertex $ 4 $ in $ 1 $ second. 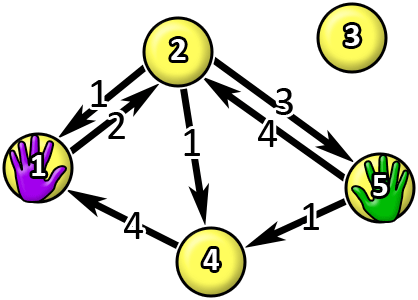 In total it needs $ 1+2+1=4 $ seconds. It can be proven that there is no other way that is faster.

**题目描述**

爱丽丝在一个有向图上进行游戏。有向图包含 $ n $ 个顶点和 $ m $ 条有向边。爱丽丝手上有一个红球和一个蓝球。游戏开始时，她将红球放在 1 号顶点，蓝球放在 $ i $ 号顶点。长度为 $ w $ 的有向边表示可以通过一次操作将 $ v $ 顶点的球移动到 $ u $ 顶点，并花费 $ w $ 的时间。在每局游戏中，爱丽丝要通过尽可能少的时间将两个球共同转移到任意同一个顶点上。爱丽丝同一时间只能操作一个球。现在爱丽丝想知道对于每个顶点 $ 2 \leq i \leq n $，每局游戏完成的最小时间是多少。

**输入格式**

输入的第一行包含两个整数 $ n $ 和 $ m $。
接下来的 $ m $ 行，每行包含三个整数 $ u $, $ v $, $ w $，表示图上有一条从 $ u $ 指向 $ v $ 长度为 $ w $ 的有向边。

**输出格式**

输出 $ n $ 行，每行一个整数，第 $ i $ 行的整数表示蓝球开始时在 $ i $ 号顶点上时游戏的最小完成时间。如果不能完成游戏，输出 -1。

**题目大意**

Pak Chanek 在玩他最喜欢的桌面游戏。在这个游戏中，有一个有 $ N $ 个顶点和 $ M $ 条边的有向图。图中的边 $ i $ 以长度 $ W_i $ 连接两个不同的顶点 $ U_i $ 和 $ V_i $。通过使用第 $ i $ 条边，可以将某物从 $ U_i $ 移动到 $ V_i $，但不能从 $ V_i $ 移动到 $ U_i $。

为了玩游戏，Pak Chanek最初必须将双手放在两个不同的顶点上。每一步，他可以将一只手移动到另一个顶点，使用一条边。要将手从顶点 $ U_i $ 移动到顶点 $ V_i $，Pak Chanek 需要花费 $ W_i $ 秒的时间。注意，Pak Chanek 一次只能移动一只手。当Pak Chanek的双手都放在同一个顶点上时，游戏结束。

Pak Chanek 有几个问题。对于每个满足 $ 2 \leq p \leq N $ 的 $ p $，你需要找到如果最初Pak Chanek的左手和右手分别放在顶点 1 和顶点 $ p $ 上时结束游戏的最低时间（以秒为单位），或者报告这是不可能的。

**输入输出格式**

**输入格式**

第一行包含两个整数 $ N $ 和 $ M $（$ 2 \leq N \leq 10^5 $，$ 0 \leq M \leq 2 \cdot 10^5 $）—— 图中的顶点数和边数。

接下来的 $ M $ 行中的第 $ i $ 行包含三个整数 $ U_i $, $ V_i $, 和 $ W_i $（$ 1 \le U_i, V_i \le N $，$ U_i \neq V_i $，$ 1 \le W_i \le 10^9 $）—— 连接两个不同顶点 $ U_i $ 和 $ V_i $，长度为 $ W_i $ 的有向边。不存在不同的边 $ i $ 和 $ j $ 使得 $ U_i = U_j $ 和 $ V_i = V_j $。

**输出格式**

输出一行，包含 $ N-1 $ 个整数。第 $ j $ 个整数表示如果最初Pak Chanek的左手和右手分别放在顶点 1 和顶点 $ j+1 $ 上时结束游戏的最低时间（以秒为单位），或者如果不可能，则为 -1。

**输入输出样例**

**输入样例 #1**

```
5 7
1 2 2
2 4 1
4 1 4
2 5 3
5 4 1
5 2 4
2 1 1
```

**输出样例 #1**

```
1 -1 3 4
```

**说明**

如果最初Pak Chanek的左手在顶点 1 上，右手在顶点 5 上，Pak Chanek 可以执行以下移动：

1. 在 1 秒内将右手移动到顶点 4。
2. 在 2 秒内将左手移动到顶点 2。
3. 在 1 秒内将左手移动到顶点 4。

总共需要 $ 1+2+1=4 $ 秒。可以证明没有更快的方式。**题目描述** 爱丽丝在一个有向图上进行游戏。有向图包含 $ n $ 个顶点和 $ m $ 条有向边。爱丽丝手上有一个红球和一个蓝球。游戏开始时，她将红球放在 1 号顶点，蓝球放在 $ i $ 号顶点。长度为 $ w $ 的有向边表示可以通过一次操作将 $ v $ 顶点的球移动到 $ u $ 顶点，并花费 $ w $ 的时间。在每局游戏中，爱丽丝要通过尽可能少的时间将两个球共同转移到任意同一个顶点上。爱丽丝同一时间只能操作一个球。现在爱丽丝想知道对于每个顶点 $ 2 \leq i \leq n $，每局游戏完成的最小时间是多少。 **输入格式** 输入的第一行包含两个整数 $ n $ 和 $ m $。 接下来的 $ m $ 行，每行包含三个整数 $ u $, $ v $, $ w $，表示图上有一条从 $ u $ 指向 $ v $ 长度为 $ w $ 的有向边。 **输出格式** 输出 $ n $ 行，每行一个整数，第 $ i $ 行的整数表示蓝球开始时在 $ i $ 号顶点上时游戏的最小完成时间。如果不能完成游戏，输出 -1。 **题目大意** Pak Chanek 在玩他最喜欢的桌面游戏。在这个游戏中，有一个有 $ N $ 个顶点和 $ M $ 条边的有向图。图中的边 $ i $ 以长度 $ W_i $ 连接两个不同的顶点 $ U_i $ 和 $ V_i $。通过使用第 $ i $ 条边，可以将某物从 $ U_i $ 移动到 $ V_i $，但不能从 $ V_i $ 移动到 $ U_i $。 为了玩游戏，Pak Chanek最初必须将双手放在两个不同的顶点上。每一步，他可以将一只手移动到另一个顶点，使用一条边。要将手从顶点 $ U_i $ 移动到顶点 $ V_i $，Pak Chanek 需要花费 $ W_i $ 秒的时间。注意，Pak Chanek 一次只能移动一只手。当Pak Chanek的双手都放在同一个顶点上时，游戏结束。 Pak Chanek 有几个问题。对于每个满足 $ 2 \leq p \leq N $ 的 $ p $，你需要找到如果最初Pak Chanek的左手和右手分别放在顶点 1 和顶点 $ p $ 上时结束游戏的最低时间（以秒为单位），或者报告这是不可能的。 **输入输出格式** **输入格式** 第一行包含两个整数 $ N $ 和 $ M $（$ 2 \leq N \leq 10^5 $，$ 0 \leq M \leq 2 \cdot 10^5 $）—— 图中的顶点数和边数。 接下来的 $ M $ 行中的第 $ i $ 行包含三个整数 $ U_i $, $ V_i $, 和 $ W_i $（$ 1 \le U_i, V_i \le N $，$ U_i \neq V_i $，$ 1 \le W_i \le 10^9 $）—— 连接两个不同顶点 $ U_i $ 和 $ V_i $，长度为 $ W_i $ 的有向边。不存在不同的边 $ i $ 和 $ j $ 使得 $ U_i = U_j $ 和 $ V_i = V_j $。 **输出格式** 输出一行，包含 $ N-1 $ 个整数。第 $ j $ 个整数表示如果最初Pak Chanek的左手和右手分别放在顶点 1 和顶点 $ j+1 $ 上时结束游戏的最低时间（以秒为单位），或者如果不可能，则为 -1。 **输入输出样例** **输入样例 #1** ``` 5 7 1 2 2 2 4 1 4 1 4 2 5 3 5 4 1 5 2 4 2 1 1 ``` **输出样例 #1** ``` 1 -1 3 4 ``` **说明** 如果最初Pak Chanek的左手在顶点 1 上，右手在顶点 5 上，Pak Chanek 可以执行以下移动： 1. 在 1 秒内将右手移动到顶点 4。 2. 在 2 秒内将左手移动到顶点 2。 3. 在 1 秒内将左手移动到顶点 4。 总共需要 $ 1+2+1=4 $ 秒。可以证明没有更快的方式。