309732: CF1726D. Edge Split
Memory Limit:256 MB
Time Limit:2 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Edge Split
题意翻译
### 题目大意 给定一个含有 $n$ 个点 $m$ 条边的无向简单图。 对这张简单图的所有边进行红蓝染色。其中**仅由红边**组成的无向图连通块数为 $c_1$,**仅由蓝边**组成的无向图连通块数为 $c_2$。 请构造一种染色方案使得 $c_1 + c_2$ 最小。如果有多种构造方案,任意输出一种即可。 ### 输入格式 第一行包含一个整数 $T \; (1 \leqslant T \leqslant 10^5)$ 表示测试样例组数。 对于每组测试样例,第一行包含两个整数 $n \; (2 \leqslant n \leqslant 2 \cdot 10^5 )$ 和 $m \; (n - 1 \leqslant m \leqslant \min(n + 2, \frac{n \cdot (n - 1)}{2}))$ 表示该简单图的点数和边数。 接下来的 m 行,含有两个数 $u_i$ 和 $v_i \; (1 \leqslant u_i,v_i \leqslant n, \; u_i \neq v_i)$ 表示点 $u_i$ 和点 $v_i$ 间存在一条有向边。数据满足图联通且不存在重边和自环。 数据满足 $\sum n \leqslant 10^6, \; \sum m \leqslant 2 \cdot 10^6$ ### 输出格式 对于每组测试样例,包含一行一个长度为 $m$ 的 $01$串 $s$ 表示其中一种满足题目条件的染色方案。其中 $s_i = 0$ 表示边 $(u_i, v_i)$ 被染成的红色,否则表示被染成了蓝色。 ### 提示 请注意 $m \leqslant n + 2$ 意味着什么。 $Translated \; by \; Zigh$题目描述
You are given a connected, undirected and unweighted graph with $ n $ vertices and $ m $ edges. Notice the limit on the number of edges: $ m \le n + 2 $ . Let's say we color some of the edges red and the remaining edges blue. Now consider only the red edges and count the number of connected components in the graph. Let this value be $ c_1 $ . Similarly, consider only the blue edges and count the number of connected components in the graph. Let this value be $ c_2 $ . Find an assignment of colors to the edges such that the quantity $ c_1+c_2 $ is minimised.输入输出格式
输入格式
Each test contains multiple test cases. The first line contains a single integer $ t $ ( $ 1 \le t \le 10^5 $ ) — the number of test cases. Description of the test cases follows. The first line of each test case contains two integers $ n $ and $ m $ ( $ 2 \le n \le 2 \cdot 10^5 $ ; $ n-1 \leq m \leq \min{\left(n+2,\frac{n \cdot (n-1)}{2}\right)} $ ) — the number of vertices and the number of edges respectively. $ m $ lines follow. The $ i $ -th line contains two integers $ u_i $ and $ v_i $ ( $ 1 \le u_i,v_i \le n $ , $ u_i \ne v_i $ ) denoting that the $ i $ -th edge goes between vertices $ u_i $ and $ v_i $ . The input is guaranteed to have no multiple edges or self loops. The graph is also guaranteed to be connected. It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 10^6 $ . It is guaranteed that the sum of $ m $ over all test cases does not exceed $ 2 \cdot 10^6 $ .
输出格式
For each test case, output a binary string of length $ m $ . The $ i $ -th character of the string should be 1 if the $ i $ -th edge should be colored red, and 0 if it should be colored blue. If there are multiple ways to assign colors to edges that give the minimum answer, you may output any.
输入输出样例
输入样例 #1
4
5 7
1 2
2 3
3 4
4 5
5 1
1 3
3 5
4 4
1 2
2 3
1 4
3 4
6 7
1 2
1 3
3 4
4 5
1 4
5 6
6 2
2 1
1 2输出样例 #1
0111010
1001
0001111
0说明
- The corresponding graph of the first test case is: 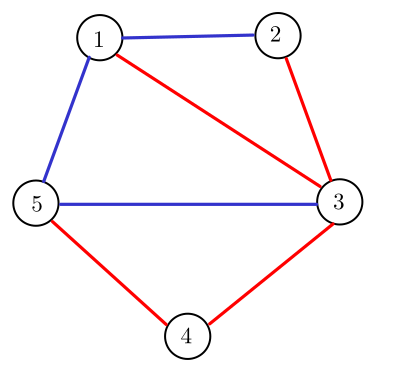 $ c_1 + c_2 = 1 + 2 = 3 $ - The corresponding graph of the second test case is: 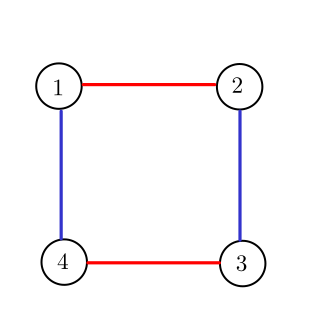 $ c_1 + c_2 = 2 + 2 = 4 $Input
题意翻译
### 题目大意 给定一个含有 $n$ 个点 $m$ 条边的无向简单图。 对这张简单图的所有边进行红蓝染色。其中**仅由红边**组成的无向图连通块数为 $c_1$,**仅由蓝边**组成的无向图连通块数为 $c_2$。 请构造一种染色方案使得 $c_1 + c_2$ 最小。如果有多种构造方案,任意输出一种即可。 ### 输入格式 第一行包含一个整数 $T \; (1 \leqslant T \leqslant 10^5)$ 表示测试样例组数。 对于每组测试样例,第一行包含两个整数 $n \; (2 \leqslant n \leqslant 2 \cdot 10^5 )$ 和 $m \; (n - 1 \leqslant m \leqslant \min(n + 2, \frac{n \cdot (n - 1)}{2}))$ 表示该简单图的点数和边数。 接下来的 m 行,含有两个数 $u_i$ 和 $v_i \; (1 \leqslant u_i,v_i \leqslant n, \; u_i \neq v_i)$ 表示点 $u_i$ 和点 $v_i$ 间存在一条有向边。数据满足图联通且不存在重边和自环。 数据满足 $\sum n \leqslant 10^6, \; \sum m \leqslant 2 \cdot 10^6$ ### 输出格式 对于每组测试样例,包含一行一个长度为 $m$ 的 $01$串 $s$ 表示其中一种满足题目条件的染色方案。其中 $s_i = 0$ 表示边 $(u_i, v_i)$ 被染成的红色,否则表示被染成了蓝色。 ### 提示 请注意 $m \leqslant n + 2$ 意味着什么。 $Translated \; by \; Zigh$Output
**题目大意**
给定一个含有 $n$ 个点 $m$ 条边的连通、无向、无权图。注意边数的限制:$m \le n + 2$。
将图中的边染色为红色或蓝色。仅考虑红色边时,图中的连通块数为 $c_1$;仅考虑蓝色边时,图中的连通块数为 $c_2$。
构造一种染色方案使得 $c_1 + c_2$ 最小。如果有多种方案,输出其中任意一种。
**输入格式**
每个测试包含多个测试案例。第一行包含一个整数 $T$($1 \le T \le 10^5$)——测试案例的数量。接下来是每个测试案例的描述。
每个测试案例的第一行包含两个整数 $n$ 和 $m$($2 \le n \le 2 \cdot 10^5$;$n-1 \le m \le \min(n+2, \frac{n \cdot (n-1)}{2})$)——顶点的数量和边的数量。
接下来 $m$ 行,每行包含两个整数 $u_i$ 和 $v_i$($1 \le u_i, v_i \le n$,$u_i \ne v_i$),表示第 $i$ 条边连接顶点 $u_i$ 和 $v_i$。输入保证没有重边或自环,且图是连通的。
保证所有测试案例的 $n$ 之和不超过 $10^6$,$m$ 之和不超过 $2 \cdot 10^6$。
**输出格式**
对于每个测试案例,输出一个长度为 $m$ 的二进制字符串。字符串的第 $i$ 个字符应为 1 如果第 $i$ 条边应染成红色,为 0 如果应染成蓝色。如果有多种给边分配颜色的方式可以得到最小答案,你可以输出任意一种。
**输入输出样例**
**输入样例 #1**
```
4
5 7
1 2
2 3
3 4
4 5
5 1
1 3
3 5
4 4
1 2
2 3
1 4
3 4
6 7
1 2
1 3
3 4
4 5
1 4
5 6
6 2
2 1
1 2
```
**输出样例 #1**
```
0111010
1001
0001111
0
```**题目大意** 给定一个含有 $n$ 个点 $m$ 条边的连通、无向、无权图。注意边数的限制:$m \le n + 2$。 将图中的边染色为红色或蓝色。仅考虑红色边时,图中的连通块数为 $c_1$;仅考虑蓝色边时,图中的连通块数为 $c_2$。 构造一种染色方案使得 $c_1 + c_2$ 最小。如果有多种方案,输出其中任意一种。 **输入格式** 每个测试包含多个测试案例。第一行包含一个整数 $T$($1 \le T \le 10^5$)——测试案例的数量。接下来是每个测试案例的描述。 每个测试案例的第一行包含两个整数 $n$ 和 $m$($2 \le n \le 2 \cdot 10^5$;$n-1 \le m \le \min(n+2, \frac{n \cdot (n-1)}{2})$)——顶点的数量和边的数量。 接下来 $m$ 行,每行包含两个整数 $u_i$ 和 $v_i$($1 \le u_i, v_i \le n$,$u_i \ne v_i$),表示第 $i$ 条边连接顶点 $u_i$ 和 $v_i$。输入保证没有重边或自环,且图是连通的。 保证所有测试案例的 $n$ 之和不超过 $10^6$,$m$ 之和不超过 $2 \cdot 10^6$。 **输出格式** 对于每个测试案例,输出一个长度为 $m$ 的二进制字符串。字符串的第 $i$ 个字符应为 1 如果第 $i$ 条边应染成红色,为 0 如果应染成蓝色。如果有多种给边分配颜色的方式可以得到最小答案,你可以输出任意一种。 **输入输出样例** **输入样例 #1** ``` 4 5 7 1 2 2 3 3 4 4 5 5 1 1 3 3 5 4 4 1 2 2 3 1 4 3 4 6 7 1 2 1 3 3 4 4 5 1 4 5 6 6 2 2 1 1 2 ``` **输出样例 #1** ``` 0111010 1001 0001111 0 ```
给定一个含有 $n$ 个点 $m$ 条边的连通、无向、无权图。注意边数的限制:$m \le n + 2$。
将图中的边染色为红色或蓝色。仅考虑红色边时,图中的连通块数为 $c_1$;仅考虑蓝色边时,图中的连通块数为 $c_2$。
构造一种染色方案使得 $c_1 + c_2$ 最小。如果有多种方案,输出其中任意一种。
**输入格式**
每个测试包含多个测试案例。第一行包含一个整数 $T$($1 \le T \le 10^5$)——测试案例的数量。接下来是每个测试案例的描述。
每个测试案例的第一行包含两个整数 $n$ 和 $m$($2 \le n \le 2 \cdot 10^5$;$n-1 \le m \le \min(n+2, \frac{n \cdot (n-1)}{2})$)——顶点的数量和边的数量。
接下来 $m$ 行,每行包含两个整数 $u_i$ 和 $v_i$($1 \le u_i, v_i \le n$,$u_i \ne v_i$),表示第 $i$ 条边连接顶点 $u_i$ 和 $v_i$。输入保证没有重边或自环,且图是连通的。
保证所有测试案例的 $n$ 之和不超过 $10^6$,$m$ 之和不超过 $2 \cdot 10^6$。
**输出格式**
对于每个测试案例,输出一个长度为 $m$ 的二进制字符串。字符串的第 $i$ 个字符应为 1 如果第 $i$ 条边应染成红色,为 0 如果应染成蓝色。如果有多种给边分配颜色的方式可以得到最小答案,你可以输出任意一种。
**输入输出样例**
**输入样例 #1**
```
4
5 7
1 2
2 3
3 4
4 5
5 1
1 3
3 5
4 4
1 2
2 3
1 4
3 4
6 7
1 2
1 3
3 4
4 5
1 4
5 6
6 2
2 1
1 2
```
**输出样例 #1**
```
0111010
1001
0001111
0
```**题目大意** 给定一个含有 $n$ 个点 $m$ 条边的连通、无向、无权图。注意边数的限制:$m \le n + 2$。 将图中的边染色为红色或蓝色。仅考虑红色边时,图中的连通块数为 $c_1$;仅考虑蓝色边时,图中的连通块数为 $c_2$。 构造一种染色方案使得 $c_1 + c_2$ 最小。如果有多种方案,输出其中任意一种。 **输入格式** 每个测试包含多个测试案例。第一行包含一个整数 $T$($1 \le T \le 10^5$)——测试案例的数量。接下来是每个测试案例的描述。 每个测试案例的第一行包含两个整数 $n$ 和 $m$($2 \le n \le 2 \cdot 10^5$;$n-1 \le m \le \min(n+2, \frac{n \cdot (n-1)}{2})$)——顶点的数量和边的数量。 接下来 $m$ 行,每行包含两个整数 $u_i$ 和 $v_i$($1 \le u_i, v_i \le n$,$u_i \ne v_i$),表示第 $i$ 条边连接顶点 $u_i$ 和 $v_i$。输入保证没有重边或自环,且图是连通的。 保证所有测试案例的 $n$ 之和不超过 $10^6$,$m$ 之和不超过 $2 \cdot 10^6$。 **输出格式** 对于每个测试案例,输出一个长度为 $m$ 的二进制字符串。字符串的第 $i$ 个字符应为 1 如果第 $i$ 条边应染成红色,为 0 如果应染成蓝色。如果有多种给边分配颜色的方式可以得到最小答案,你可以输出任意一种。 **输入输出样例** **输入样例 #1** ``` 4 5 7 1 2 2 3 3 4 4 5 5 1 1 3 3 5 4 4 1 2 2 3 1 4 3 4 6 7 1 2 1 3 3 4 4 5 1 4 5 6 6 2 2 1 1 2 ``` **输出样例 #1** ``` 0111010 1001 0001111 0 ```