Ela Goes Hiking

题意翻译

$n$ 只蚂蚁站成一排，第 $1$ 只蚂蚁左边和第 $n$只蚂蚁右边各有一个挡板，相邻两只蚂蚁的距离、第 $1$ 只蚂蚁与左边挡板的距离和第 $n$ 只蚂蚁与右侧挡板的距离相等。初始时每只蚂蚁重量相等，每只蚂蚁有 $\frac{1}{2}$ 概率向左运动，$\frac{1}{2}$ 概率向右运动，每只蚂蚁速度相同。中途蚂蚁不可主动改变方向，如果碰到挡板则向相反方向运动，若两只蚂蚁相遇，重量大的蚂蚁会把重量小的蚂蚁吃掉，重量变为两者之和，如果重量相同，向左运动的蚂蚁会吃掉向右运动的蚂蚁。求对于所有 $i\le1\le n$，第 $i$ 只蚂蚁成为最终的存活者的概率对 $10^9+7$ 取模。

题目描述

Ela likes to go hiking a lot. She loves nature and exploring the various creatures it offers. One day, she saw a strange type of ant, with a cannibalistic feature. More specifically, an ant would eat any ants that it sees which is smaller than it.Curious about this feature from a new creature, Ela ain't furious. She conducts a long, non-dubious, sentimental experiment. She puts $ n $ cannibalistic ants in a line on a long wooden stick. Initially, the ants have the same weight of $ 1 $ . The distance between any two consecutive ants is the same. The distance between the first ant in the line to the left end and the last ant in the line to the right end is also the same as the distance between the ants. Each ant starts moving towards the left-end or the right-end randomly and equiprobably, at the same constant pace throughout the experiment. Two ants will crash if they are standing next to each other in the line and moving in opposite directions, and ants will change direction immediately when they reach the end of the stick. Ela can't determine the moving direction of each ant, but she understands very well their behavior when crashes happen. - If a crash happens between two ants of different weights, the heavier one will eat the lighter one, and gain the weight of the lighter one. After that, the heavier and will continue walking in the same direction. In other words, if the heavier one has weight $ x $ and walking to the right, the lighter one has weight $ y $ and walking to the left ( $ x > y $ ), then after the crash, the lighter one will diminish, and the heavier one will have weight $ x + y $ and continue walking to the right. - If a crash happens between two ants with the same weight, the one walking to the left end of the stick will eat the one walking to the right, and then continue walking in the same direction. In other words, if one ant of weight $ x $ walking to the left, crashes with another ant of weight $ x $ walking to the right, the one walking to the right will disappear, and the one walking to the left will have to weight $ 2x $ and continue walking to the left. Please, check the example in the "Note" section, which will demonstrate the ants' behavior as above. We can prove that after a definite amount of time, there will be only one last ant standing. Initially, each ant can randomly and equiprobably move to the left or the right, which generates $ 2^n $ different cases of initial movements for the whole pack. For each position in the line, calculate the probability that the ant begins in that position and survives. Output it modulo $ 10^9 + 7 $ . Formally, let $ M = 10^9 + 7 $ . It can be shown that the answer can be expressed as an irreducible fraction $ \frac{p}{q} $ , where $ p $ and $ q $ are integers and $ q \not \equiv 0 \pmod{M} $ . Output the integer equal to $ p \cdot q^{-1} \bmod M $ . In other words, output such an integer $ x $ that $ 0 \le x < M $ and $ x \cdot q \equiv p \pmod{M} $ .

输入输出格式

输入格式

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10^3 $ ). The description of the test cases follows. The only line of each test contains an integer $ n $ ( $ 1 \le n \le 10^6 $ ) — the number of ants in the experiment. It is guaranteed that the sum of $ n $ in all tests will not exceed $ 10^6 $ .

输出格式

For each test, print $ n $ lines. $ i $ -th line contains a single number that denotes the survival probability of the $ i $ -th ant in the line modulo $ 10^9 + 7 $ .

输入输出样例

输入样例 #1

3
4
5
2

输出样例 #1

0
250000002
250000002
500000004
0
250000002
250000002
250000002
250000002
0
1

说明

Here is the example of $ 6 $ ants moving on the branch. An ant's movement will be denoted by either a character $ L $ or $ R $ . Initially, the pack of ants on the branch will move as $ RLRRLR $ . Here's how the behavior of the pack demonstrated: Initially, the ants are positioned as above. After a while, the ant with index $ 2 $ (walking to the left) will crash with the ant with index $ 1 $ (walking to the right). The two ants have the same weight, therefore, ant $ 2 $ will eat ant $ 1 $ and gain its weight to $ 2 $ . The same thing happens with ant $ 5 $ and ant $ 4 $ . The ant $ 6 $ will walk to the end of the stick, therefore changing its direction. After that, the ant with index $ 5 $ will crash with the ant with index $ 3 $ . Since ant $ 5 $ is more heavy (weight= $ 2 $ ) than ant $ 3 $ (weight= $ 1 $ ), ant $ 5 $ will eat ant $ 3 $ and gain its weight to $ 3 $ . Ant $ 2 $ will walk to the end of the stick, therefore changing its direction. 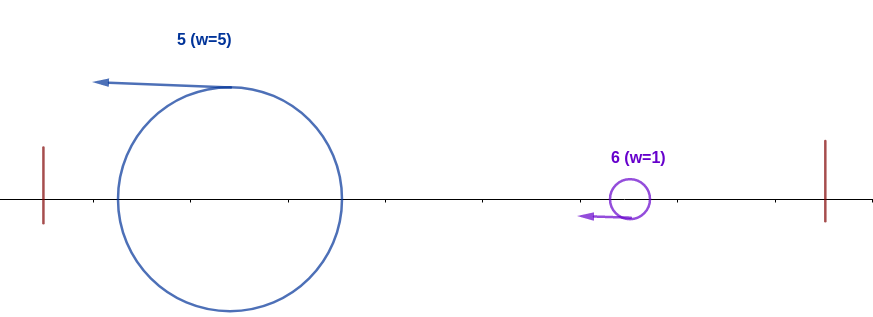After that, the ant with index $ 5 $ will crash with the ant with index $ 2 $ . Since ant $ 5 $ is more heavy (weight= $ 3 $ ) than ant $ 2 $ (weight= $ 2 $ ), ant $ 5 $ will eat ant $ 2 $ and gain its weight to $ 5 $ . 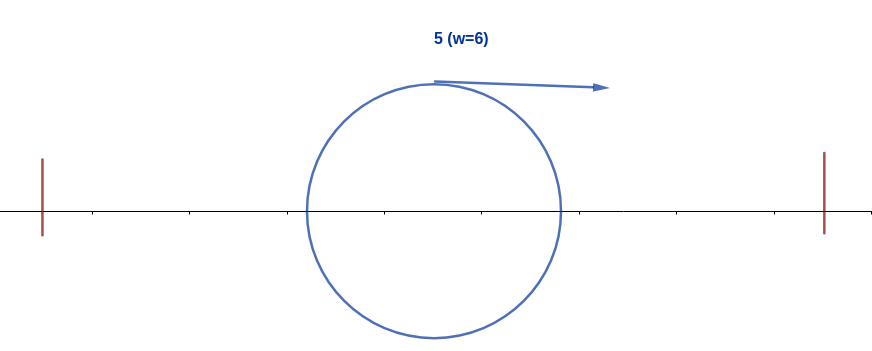Lastly, after ant $ 5 $ walk to the end of the branch and changes its direction, ant $ 5 $ will eat ant $ 6 $ and be the last ant standing.

**题意翻译**

有 $ n $ 只蚂蚁排成一行，每只蚂蚁的初始重量相同。蚂蚁在每一步中随机选择向左或向右移动，速度相同。如果蚂蚁相遇，重量较大的蚂蚁会吃掉重量较小的蚂蚁并增加相应的重量；如果重量相同，向左的蚂蚁会吃掉向右的蚂蚁。求每只蚂蚁最终存活下来的概率，结果对 $ 10^9+7 $ 取模。

**输入输出格式**

**输入格式**

每个测试包含多个测试案例。第一行包含测试案例的数量 $ t $（$ 1 \le t \le 10^3 $）。接下来每行包含一个整数 $ n $（$ 1 \le n \le 10^6 $）表示实验中蚂蚁的数量。所有测试中 $ n $ 的总和不超过 $ 10^6 $。

**输出格式**

对于每个测试，输出 $ n $ 行。第 $ i $ 行包含一个数字，表示第 $ i $ 只蚂蚁存活下来的概率，结果对 $ 10^9+7 $ 取模。**题意翻译** 有 $ n $ 只蚂蚁排成一行，每只蚂蚁的初始重量相同。蚂蚁在每一步中随机选择向左或向右移动，速度相同。如果蚂蚁相遇，重量较大的蚂蚁会吃掉重量较小的蚂蚁并增加相应的重量；如果重量相同，向左的蚂蚁会吃掉向右的蚂蚁。求每只蚂蚁最终存活下来的概率，结果对 $ 10^9+7 $ 取模。 **输入输出格式** **输入格式** 每个测试包含多个测试案例。第一行包含测试案例的数量 $ t $（$ 1 \le t \le 10^3 $）。接下来每行包含一个整数 $ n $（$ 1 \le n \le 10^6 $）表示实验中蚂蚁的数量。所有测试中 $ n $ 的总和不超过 $ 10^6 $。 **输出格式** 对于每个测试，输出 $ n $ 行。第 $ i $ 行包含一个数字，表示第 $ i $ 只蚂蚁存活下来的概率，结果对 $ 10^9+7 $ 取模。