309835: CF1742E. Scuza
Memory Limit:256 MB
Time Limit:3 S
Judge Style:Text Compare
Creator:
Submit:9
Solved:0
Description
Scuza
题意翻译
有 $n$ 阶楼梯,当前楼梯与上一阶楼梯的高度差为 $a_i$($a_1$ 就是第一节阶梯的高度)。 $q$ 次询问,对于每一个 $k_i\ (1\le i \le q)$,若 Timur 一步能提高 $k_i$ 的高度,求出他能到达的最高高度。题目描述
Timur has a stairway with $ n $ steps. The $ i $ -th step is $ a_i $ meters higher than its predecessor. The first step is $ a_1 $ meters higher than the ground, and the ground starts at $ 0 $ meters. 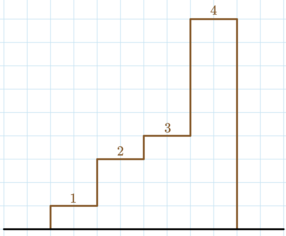The stairs for the first test case.Timur has $ q $ questions, each denoted by an integer $ k_1, \dots, k_q $ . For each question $ k_i $ , you have to print the maximum possible height Timur can achieve by climbing the steps if his legs are of length $ k_i $ . Timur can only climb the $ j $ -th step if his legs are of length at least $ a_j $ . In other words, $ k_i \geq a_j $ for each step $ j $ climbed. Note that you should answer each question independently.输入输出格式
输入格式
The first line contains a single integer $ t $ ( $ 1 \leq t \leq 100 $ ) — the number of test cases. The first line of each test case contains two integers $ n, q $ ( $ 1 \leq n, q \leq 2\cdot10^5 $ ) — the number of steps and the number of questions, respectively. The second line of each test case contains $ n $ integers ( $ 1 \leq a_i \leq 10^9 $ ) — the height of the steps. The third line of each test case contains $ q $ integers ( $ 0 \leq k_i \leq 10^9 $ ) — the numbers for each question. It is guaranteed that the sum of $ n $ does not exceed $ 2\cdot10^5 $ , and the sum of $ q $ does not exceed $ 2\cdot10^5 $ .
输出格式
For each test case, output a single line containing $ q $ integers, the answer for each question. Please note, that the answer for some questions won't fit into 32-bit integer type, so you should use at least 64-bit integer type in your programming language (like long long for C++).
输入输出样例
输入样例 #1
3
4 5
1 2 1 5
1 2 4 9 10
2 2
1 1
0 1
3 1
1000000000 1000000000 1000000000
1000000000输出样例 #1
1 4 4 9 9
0 2
3000000000说明
Consider the first test case, pictured in the statement. - If Timur's legs have length $ 1 $ , then he can only climb stair $ 1 $ , so the highest he can reach is $ 1 $ meter. - If Timur's legs have length $ 2 $ or $ 4 $ , then he can only climb stairs $ 1 $ , $ 2 $ , and $ 3 $ , so the highest he can reach is $ 1+2+1=4 $ meters. - If Timur's legs have length $ 9 $ or $ 10 $ , then he can climb the whole staircase, so the highest he can reach is $ 1+2+1+5=9 $ meters. In the first question of the second test case, Timur has no legs, so he cannot go up even a single step. :(Input
题意翻译
有 $n$ 阶楼梯,当前楼梯与上一阶楼梯的高度差为 $a_i$($a_1$ 就是第一节阶梯的高度)。 $q$ 次询问,对于每一个 $k_i\ (1\le i \le q)$,若 Timur 一步能提高 $k_i$ 的高度,求出他能到达的最高高度。Output
**题意翻译**
有 $n$ 阶楼梯,每一阶楼梯与上一阶楼梯的高度差为 $a_i$($a_1$ 是第一节阶梯的高度)。
$q$ 次询问,对于每一个 $k_i\ (1\le i \le q)$,如果 Timur 一步能提高 $k_i$ 的高度,求出他能到达的最高高度。
**题目描述**
Timur 有一个 $n$ 阶的楼梯。第 $i$ 阶楼梯比前一级高 $a_i$ 米。第一节楼梯比地面高 $a_1$ 米,地面高度为 $0$ 米。
Timur 有 $q$ 个问题,每个问题用一个整数 $k_1, \dots, k_q$ 表示。对于每个问题 $k_i$,你需要打印出如果 Timur 的腿长为 $k_i$,他能够通过爬楼梯达到的最大高度。Timur 只有在腿长至少为 $a_j$ 的情况下才能爬上第 $j$ 阶楼梯。换句话说,对于爬上的每一阶 $j$,必须满足 $k_i \geq a_j$。
注意,你应该独立回答每个问题。
**输入输出格式**
**输入格式**
第一行包含一个整数 $t$($1 \leq t \leq 100$)——测试用例的数量。
每个测试用例的第一行包含两个整数 $n, q$($1 \leq n, q \leq 2\cdot10^5$)——楼梯的阶数和问题的数量。
每个测试用例的第二行包含 $n$ 个整数($1 \leq a_i \leq 10^9$)——楼梯的高度。
每个测试用例的第三行包含 $q$ 个整数($0 \leq k_i \leq 10^9$)——每个问题的数字。
保证 $n$ 的总和不超过 $2\cdot10^5$,$q$ 的总和不超过 $2\cdot10^5$。
**输出格式**
对于每个测试用例,输出一行包含 $q$ 个整数,即每个问题的答案。
请注意,某些问题的答案可能不适合 32 位整数类型,因此你应在编程语言中使用至少 64 位整数类型(例如 C++ 中的 long long)。
**输入输出样例**
**输入样例 #1**
```
3
4 5
1 2 1 5
1 2 4 9 10
2 2
1 1
0 1
3 1
1000000000 1000000000 1000000000
1000000000
```
**输出样例 #1**
```
1 4 4 9 9
0 2
3000000000
```
**说明**
考虑第一个测试用例,在题目描述中有图示。
- 如果 Timur 的腿长为 1,那么他只能爬上第 1 阶,所以他能达到的最高高度是 1 米。
- 如果 Timur 的腿长为 2 或 4,那么他只能爬上第 1、2、3 阶,所以他能达到的最高高度是 $1+2+1=4$ 米。
- 如果 Timur 的腿长为 9 或 10,那么他可以爬完整座楼梯,所以他能达到的最高高度是 $1+2+1+5=9$ 米。
在第二个测试用例的第一个问题中,Timur 没有腿,所以他甚至不能爬上一阶楼梯。:(**题意翻译** 有 $n$ 阶楼梯,每一阶楼梯与上一阶楼梯的高度差为 $a_i$($a_1$ 是第一节阶梯的高度)。 $q$ 次询问,对于每一个 $k_i\ (1\le i \le q)$,如果 Timur 一步能提高 $k_i$ 的高度,求出他能到达的最高高度。 **题目描述** Timur 有一个 $n$ 阶的楼梯。第 $i$ 阶楼梯比前一级高 $a_i$ 米。第一节楼梯比地面高 $a_1$ 米,地面高度为 $0$ 米。 Timur 有 $q$ 个问题,每个问题用一个整数 $k_1, \dots, k_q$ 表示。对于每个问题 $k_i$,你需要打印出如果 Timur 的腿长为 $k_i$,他能够通过爬楼梯达到的最大高度。Timur 只有在腿长至少为 $a_j$ 的情况下才能爬上第 $j$ 阶楼梯。换句话说,对于爬上的每一阶 $j$,必须满足 $k_i \geq a_j$。 注意,你应该独立回答每个问题。 **输入输出格式** **输入格式** 第一行包含一个整数 $t$($1 \leq t \leq 100$)——测试用例的数量。 每个测试用例的第一行包含两个整数 $n, q$($1 \leq n, q \leq 2\cdot10^5$)——楼梯的阶数和问题的数量。 每个测试用例的第二行包含 $n$ 个整数($1 \leq a_i \leq 10^9$)——楼梯的高度。 每个测试用例的第三行包含 $q$ 个整数($0 \leq k_i \leq 10^9$)——每个问题的数字。 保证 $n$ 的总和不超过 $2\cdot10^5$,$q$ 的总和不超过 $2\cdot10^5$。 **输出格式** 对于每个测试用例,输出一行包含 $q$ 个整数,即每个问题的答案。 请注意,某些问题的答案可能不适合 32 位整数类型,因此你应在编程语言中使用至少 64 位整数类型(例如 C++ 中的 long long)。 **输入输出样例** **输入样例 #1** ``` 3 4 5 1 2 1 5 1 2 4 9 10 2 2 1 1 0 1 3 1 1000000000 1000000000 1000000000 1000000000 ``` **输出样例 #1** ``` 1 4 4 9 9 0 2 3000000000 ``` **说明** 考虑第一个测试用例,在题目描述中有图示。 - 如果 Timur 的腿长为 1,那么他只能爬上第 1 阶,所以他能达到的最高高度是 1 米。 - 如果 Timur 的腿长为 2 或 4,那么他只能爬上第 1、2、3 阶,所以他能达到的最高高度是 $1+2+1=4$ 米。 - 如果 Timur 的腿长为 9 或 10,那么他可以爬完整座楼梯,所以他能达到的最高高度是 $1+2+1+5=9$ 米。 在第二个测试用例的第一个问题中,Timur 没有腿,所以他甚至不能爬上一阶楼梯。:(
有 $n$ 阶楼梯,每一阶楼梯与上一阶楼梯的高度差为 $a_i$($a_1$ 是第一节阶梯的高度)。
$q$ 次询问,对于每一个 $k_i\ (1\le i \le q)$,如果 Timur 一步能提高 $k_i$ 的高度,求出他能到达的最高高度。
**题目描述**
Timur 有一个 $n$ 阶的楼梯。第 $i$ 阶楼梯比前一级高 $a_i$ 米。第一节楼梯比地面高 $a_1$ 米,地面高度为 $0$ 米。
Timur 有 $q$ 个问题,每个问题用一个整数 $k_1, \dots, k_q$ 表示。对于每个问题 $k_i$,你需要打印出如果 Timur 的腿长为 $k_i$,他能够通过爬楼梯达到的最大高度。Timur 只有在腿长至少为 $a_j$ 的情况下才能爬上第 $j$ 阶楼梯。换句话说,对于爬上的每一阶 $j$,必须满足 $k_i \geq a_j$。
注意,你应该独立回答每个问题。
**输入输出格式**
**输入格式**
第一行包含一个整数 $t$($1 \leq t \leq 100$)——测试用例的数量。
每个测试用例的第一行包含两个整数 $n, q$($1 \leq n, q \leq 2\cdot10^5$)——楼梯的阶数和问题的数量。
每个测试用例的第二行包含 $n$ 个整数($1 \leq a_i \leq 10^9$)——楼梯的高度。
每个测试用例的第三行包含 $q$ 个整数($0 \leq k_i \leq 10^9$)——每个问题的数字。
保证 $n$ 的总和不超过 $2\cdot10^5$,$q$ 的总和不超过 $2\cdot10^5$。
**输出格式**
对于每个测试用例,输出一行包含 $q$ 个整数,即每个问题的答案。
请注意,某些问题的答案可能不适合 32 位整数类型,因此你应在编程语言中使用至少 64 位整数类型(例如 C++ 中的 long long)。
**输入输出样例**
**输入样例 #1**
```
3
4 5
1 2 1 5
1 2 4 9 10
2 2
1 1
0 1
3 1
1000000000 1000000000 1000000000
1000000000
```
**输出样例 #1**
```
1 4 4 9 9
0 2
3000000000
```
**说明**
考虑第一个测试用例,在题目描述中有图示。
- 如果 Timur 的腿长为 1,那么他只能爬上第 1 阶,所以他能达到的最高高度是 1 米。
- 如果 Timur 的腿长为 2 或 4,那么他只能爬上第 1、2、3 阶,所以他能达到的最高高度是 $1+2+1=4$ 米。
- 如果 Timur 的腿长为 9 或 10,那么他可以爬完整座楼梯,所以他能达到的最高高度是 $1+2+1+5=9$ 米。
在第二个测试用例的第一个问题中,Timur 没有腿,所以他甚至不能爬上一阶楼梯。:(**题意翻译** 有 $n$ 阶楼梯,每一阶楼梯与上一阶楼梯的高度差为 $a_i$($a_1$ 是第一节阶梯的高度)。 $q$ 次询问,对于每一个 $k_i\ (1\le i \le q)$,如果 Timur 一步能提高 $k_i$ 的高度,求出他能到达的最高高度。 **题目描述** Timur 有一个 $n$ 阶的楼梯。第 $i$ 阶楼梯比前一级高 $a_i$ 米。第一节楼梯比地面高 $a_1$ 米,地面高度为 $0$ 米。 Timur 有 $q$ 个问题,每个问题用一个整数 $k_1, \dots, k_q$ 表示。对于每个问题 $k_i$,你需要打印出如果 Timur 的腿长为 $k_i$,他能够通过爬楼梯达到的最大高度。Timur 只有在腿长至少为 $a_j$ 的情况下才能爬上第 $j$ 阶楼梯。换句话说,对于爬上的每一阶 $j$,必须满足 $k_i \geq a_j$。 注意,你应该独立回答每个问题。 **输入输出格式** **输入格式** 第一行包含一个整数 $t$($1 \leq t \leq 100$)——测试用例的数量。 每个测试用例的第一行包含两个整数 $n, q$($1 \leq n, q \leq 2\cdot10^5$)——楼梯的阶数和问题的数量。 每个测试用例的第二行包含 $n$ 个整数($1 \leq a_i \leq 10^9$)——楼梯的高度。 每个测试用例的第三行包含 $q$ 个整数($0 \leq k_i \leq 10^9$)——每个问题的数字。 保证 $n$ 的总和不超过 $2\cdot10^5$,$q$ 的总和不超过 $2\cdot10^5$。 **输出格式** 对于每个测试用例,输出一行包含 $q$ 个整数,即每个问题的答案。 请注意,某些问题的答案可能不适合 32 位整数类型,因此你应在编程语言中使用至少 64 位整数类型(例如 C++ 中的 long long)。 **输入输出样例** **输入样例 #1** ``` 3 4 5 1 2 1 5 1 2 4 9 10 2 2 1 1 0 1 3 1 1000000000 1000000000 1000000000 1000000000 ``` **输出样例 #1** ``` 1 4 4 9 9 0 2 3000000000 ``` **说明** 考虑第一个测试用例,在题目描述中有图示。 - 如果 Timur 的腿长为 1,那么他只能爬上第 1 阶,所以他能达到的最高高度是 1 米。 - 如果 Timur 的腿长为 2 或 4,那么他只能爬上第 1、2、3 阶,所以他能达到的最高高度是 $1+2+1=4$ 米。 - 如果 Timur 的腿长为 9 或 10,那么他可以爬完整座楼梯,所以他能达到的最高高度是 $1+2+1+5=9$ 米。 在第二个测试用例的第一个问题中,Timur 没有腿,所以他甚至不能爬上一阶楼梯。:(