309946: CF1763E. Node Pairs
Memory Limit:256 MB
Time Limit:2 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Node Pairs
题意翻译
在一个有向图中,一个节点对 $ ( u , v ) $ 如果满足 $ u \ne v $,$ u $ 能到达 $ v $ 且 $ v $ 不能到达 $ u $,则称其为单向节点对。 如果一个有向图刚好存在 $ p $ 对节点 $ ( u , v) $($ u < v $ 且二者能互相到达),则称这是一个 $ p $ 可达图,求节点最少的 $ p $ 可达图的节点数。 同时,定义图 $ G $ 为在所有节点数最少的 $ p $ 可达图中,单向节点对数量最多的图,求出图 $ G $ 中单向节点对的个数。题目描述
Let's call an ordered pair of nodes $ (u, v) $ in a directed graph unidirectional if $ u \neq v $ , there exists a path from $ u $ to $ v $ , and there are no paths from $ v $ to $ u $ . A directed graph is called $ p $ -reachable if it contains exactly $ p $ ordered pairs of nodes $ (u, v) $ such that $ u < v $ and $ u $ and $ v $ are reachable from each other. Find the minimum number of nodes required to create a $ p $ -reachable directed graph. Also, among all such $ p $ -reachable directed graphs with the minimum number of nodes, let $ G $ denote a graph which maximizes the number of unidirectional pairs of nodes. Find this number.输入输出格式
输入格式
The first and only line contains a single integer $ p $ ( $ 0 \le p \le 2 \cdot 10^5 $ ) — the number of ordered pairs of nodes.
输出格式
Print a single line containing two integers — the minimum number of nodes required to create a $ p $ -reachable directed graph, and the maximum number of unidirectional pairs of nodes among all such $ p $ -reachable directed graphs with the minimum number of nodes.
输入输出样例
输入样例 #1
3输出样例 #1
3 0输入样例 #2
4输出样例 #2
5 6输入样例 #3
0输出样例 #3
0 0说明
In the first test case, the minimum number of nodes required to create a $ 3 $ -reachable directed graph is $ 3 $ . Among all $ 3 $ -reachable directed graphs with $ 3 $ nodes, the following graph $ G $ is one of the graphs with the maximum number of unidirectional pairs of nodes, which is $ 0 $ . 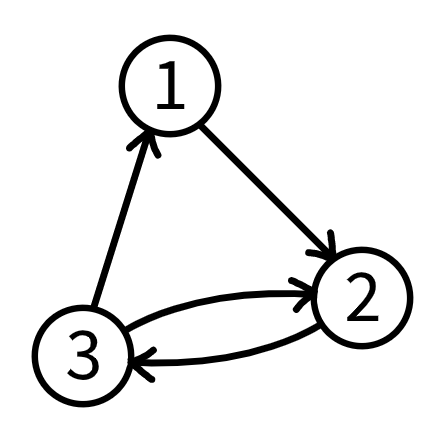Input
题意翻译
在一个有向图中,一个节点对 $ ( u , v ) $ 如果满足 $ u \ne v $,$ u $ 能到达 $ v $ 且 $ v $ 不能到达 $ u $,则称其为单向节点对。 如果一个有向图刚好存在 $ p $ 对节点 $ ( u , v) $($ u < v $ 且二者能互相到达),则称这是一个 $ p $ 可达图,求节点最少的 $ p $ 可达图的节点数。 同时,定义图 $ G $ 为在所有节点数最少的 $ p $ 可达图中,单向节点对数量最多的图,求出图 $ G $ 中单向节点对的个数。Output
题目大意:
在有向图中,如果存在一个节点对 $ (u, v) $ 满足 $ u \neq v $,且从 $ u $ 到 $ v $ 有路径,但从 $ v $ 到 $ u $ 没有路径,则称这个节点对为单向节点对。如果图中恰好存在 $ p $ 对节点 $ (u, v) $($ u < v $ 且两节点互相可达),则称该图为 $ p $ 可达图。求出节点数最少的 $ p $ 可达图的节点数。在所有节点数最少的 $ p $ 可达图中,找出单向节点对数量最多的图 $ G $,并求出该图中单向节点对的数量。
输入输出数据格式:
- 输入格式:第一行包含一个整数 $ p $($ 0 \le p \le 2 \cdot 10^5 $),表示节点对的数目。
- 输出格式:输出一行两个整数,第一个整数表示创建 $ p $ 可达图所需的最少节点数,第二个整数表示在所有节点数最少的 $ p $ 可达图中,单向节点对数量的最大值。题目大意: 在有向图中,如果存在一个节点对 $ (u, v) $ 满足 $ u \neq v $,且从 $ u $ 到 $ v $ 有路径,但从 $ v $ 到 $ u $ 没有路径,则称这个节点对为单向节点对。如果图中恰好存在 $ p $ 对节点 $ (u, v) $($ u < v $ 且两节点互相可达),则称该图为 $ p $ 可达图。求出节点数最少的 $ p $ 可达图的节点数。在所有节点数最少的 $ p $ 可达图中,找出单向节点对数量最多的图 $ G $,并求出该图中单向节点对的数量。 输入输出数据格式: - 输入格式:第一行包含一个整数 $ p $($ 0 \le p \le 2 \cdot 10^5 $),表示节点对的数目。 - 输出格式:输出一行两个整数,第一个整数表示创建 $ p $ 可达图所需的最少节点数,第二个整数表示在所有节点数最少的 $ p $ 可达图中,单向节点对数量的最大值。
在有向图中,如果存在一个节点对 $ (u, v) $ 满足 $ u \neq v $,且从 $ u $ 到 $ v $ 有路径,但从 $ v $ 到 $ u $ 没有路径,则称这个节点对为单向节点对。如果图中恰好存在 $ p $ 对节点 $ (u, v) $($ u < v $ 且两节点互相可达),则称该图为 $ p $ 可达图。求出节点数最少的 $ p $ 可达图的节点数。在所有节点数最少的 $ p $ 可达图中,找出单向节点对数量最多的图 $ G $,并求出该图中单向节点对的数量。
输入输出数据格式:
- 输入格式:第一行包含一个整数 $ p $($ 0 \le p \le 2 \cdot 10^5 $),表示节点对的数目。
- 输出格式:输出一行两个整数,第一个整数表示创建 $ p $ 可达图所需的最少节点数,第二个整数表示在所有节点数最少的 $ p $ 可达图中,单向节点对数量的最大值。题目大意: 在有向图中,如果存在一个节点对 $ (u, v) $ 满足 $ u \neq v $,且从 $ u $ 到 $ v $ 有路径,但从 $ v $ 到 $ u $ 没有路径,则称这个节点对为单向节点对。如果图中恰好存在 $ p $ 对节点 $ (u, v) $($ u < v $ 且两节点互相可达),则称该图为 $ p $ 可达图。求出节点数最少的 $ p $ 可达图的节点数。在所有节点数最少的 $ p $ 可达图中,找出单向节点对数量最多的图 $ G $,并求出该图中单向节点对的数量。 输入输出数据格式: - 输入格式:第一行包含一个整数 $ p $($ 0 \le p \le 2 \cdot 10^5 $),表示节点对的数目。 - 输出格式:输出一行两个整数,第一个整数表示创建 $ p $ 可达图所需的最少节点数,第二个整数表示在所有节点数最少的 $ p $ 可达图中,单向节点对数量的最大值。