309950: CF1764C. Doremy's City Construction
Memory Limit:256 MB
Time Limit:1 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Doremy's City Construction
题意翻译
有一些点,每个点有一个点权 $a_i$, 你可以在任意两个点间连边。最终你连成的图需要满足:不存在点 $u, v, w$,满足 $a_u\leq a_v\leq a_w$ 且边 $(u, v), (v, w)$ 存在。求最多能连的边数。 Translated by Microchip2333.题目描述
Doremy's new city is under construction! The city can be regarded as a simple undirected graph with $ n $ vertices. The $ i $ -th vertex has altitude $ a_i $ . Now Doremy is deciding which pairs of vertices should be connected with edges. Due to economic reasons, there should be no self-loops or multiple edges in the graph. Due to safety reasons, there should not be pairwise distinct vertices $ u $ , $ v $ , and $ w $ such that $ a_u \leq a_v \leq a_w $ and the edges $ (u,v) $ and $ (v,w) $ exist. Under these constraints, Doremy would like to know the maximum possible number of edges in the graph. Can you help her? Note that the constructed graph is allowed to be disconnected.输入输出格式
输入格式
The input consists of multiple test cases. The first line contains a single integer $ t $ ( $ 1\le t\le 10^4 $ ) — the number of test cases. The description of the test cases follows. The first line of each test case contains a single integer $ n $ ( $ 2 \le n \le 2\cdot 10^5 $ ) — the number of vertices. The second line of each test case contains $ n $ integers $ a_1, a_2, \dots, a_n $ ( $ 1\le a_i\le 10^6 $ ) — the altitudes of each vertex. It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 2 \cdot 10^5 $ .
输出格式
For each test case, output the maximum possible number of edges in the graph.
输入输出样例
输入样例 #1
4
4
2 2 3 1
6
5 2 3 1 5 2
12
7 2 4 9 1 4 6 3 7 4 2 3
4
1000000 1000000 1000000 1000000输出样例 #1
3
9
35
2说明
In the first test case, there can only be at most $ 3 $ edges in the graph. A possible construction is to connect $ (1,3) $ , $ (2,3) $ , $ (3,4) $ . In the picture below the red number above node $ i $ is $ a_i $ . 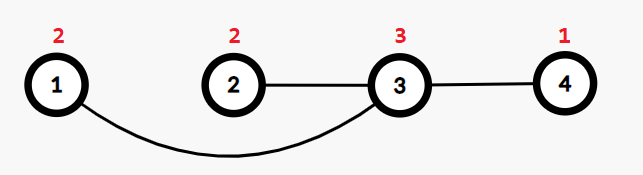 The following list shows all such $ u $ , $ v $ , $ w $ that the edges $ (u,v) $ and $ (v,w) $ exist. - $ u=1 $ , $ v=3 $ , $ w=2 $ ; - $ u=1 $ , $ v=3 $ , $ w=4 $ ; - $ u=2 $ , $ v=3 $ , $ w=1 $ ; - $ u=2 $ , $ v=3 $ , $ w=4 $ ; - $ u=4 $ , $ v=3 $ , $ w=1 $ ; - $ u=4 $ , $ v=3 $ , $ w=2 $ . Another possible construction is to connect $ (1,4) $ , $ (2,4) $ , $ (3,4) $ . 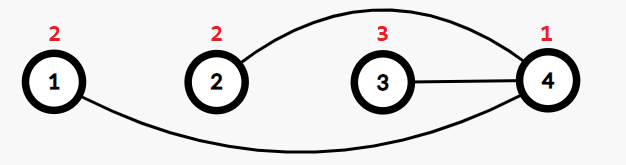 An unacceptable construction is to connect $ (1,3) $ , $ (2,3) $ , $ (2,4) $ , $ (3,4) $ . Because when $ u=4 $ , $ v=2 $ , $ w=3 $ , $ a_u\le a_v \le a_w $ holds, and the respective edges exist. 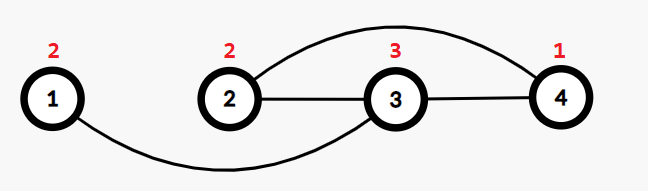Input
题意翻译
有一些点,每个点有一个点权 $a_i$, 你可以在任意两个点间连边。最终你连成的图需要满足:不存在点 $u, v, w$,满足 $a_u\leq a_v\leq a_w$ 且边 $(u, v), (v, w)$ 存在。求最多能连的边数。 Translated by Microchip2333.Output
**题目大意:**
多雷米的新城市正在建设中!该城市可以被视为一个具有n个顶点的简单无向图。第i个顶点的高度为a_i。现在多雷米正在决定哪些顶点对应该用边连接。
由于经济原因,图中不应有自环或多重边。
出于安全原因,不应存在三个互不相同的顶点u、v和w,使得a_u ≤ a_v ≤ a_w,并且边(u,v)和(v,w)都存在。
在这些约束条件下,多雷米想知道图中可能的最大边数。你能帮她吗?
注意,构建的图可以是非连通的。
**输入输出数据格式:**
**输入格式:**
输入由多个测试案例组成。第一行包含一个整数t(1≤t≤10^4)——测试案例的数量。接下来是每个测试案例的描述。
每个测试案例的第一行包含一个整数n(2≤n≤2×10^5)——顶点的数量。
每个测试案例的第二行包含n个整数a_1, a_2, …, a_n(1≤a_i≤10^6)——每个顶点的高度。
保证所有测试案例的n之和不超过2×10^5。
**输出格式:**
对于每个测试案例,输出图中可能的最大边数。**题目大意:** 多雷米的新城市正在建设中!该城市可以被视为一个具有n个顶点的简单无向图。第i个顶点的高度为a_i。现在多雷米正在决定哪些顶点对应该用边连接。 由于经济原因,图中不应有自环或多重边。 出于安全原因,不应存在三个互不相同的顶点u、v和w,使得a_u ≤ a_v ≤ a_w,并且边(u,v)和(v,w)都存在。 在这些约束条件下,多雷米想知道图中可能的最大边数。你能帮她吗? 注意,构建的图可以是非连通的。 **输入输出数据格式:** **输入格式:** 输入由多个测试案例组成。第一行包含一个整数t(1≤t≤10^4)——测试案例的数量。接下来是每个测试案例的描述。 每个测试案例的第一行包含一个整数n(2≤n≤2×10^5)——顶点的数量。 每个测试案例的第二行包含n个整数a_1, a_2, …, a_n(1≤a_i≤10^6)——每个顶点的高度。 保证所有测试案例的n之和不超过2×10^5。 **输出格式:** 对于每个测试案例,输出图中可能的最大边数。
多雷米的新城市正在建设中!该城市可以被视为一个具有n个顶点的简单无向图。第i个顶点的高度为a_i。现在多雷米正在决定哪些顶点对应该用边连接。
由于经济原因,图中不应有自环或多重边。
出于安全原因,不应存在三个互不相同的顶点u、v和w,使得a_u ≤ a_v ≤ a_w,并且边(u,v)和(v,w)都存在。
在这些约束条件下,多雷米想知道图中可能的最大边数。你能帮她吗?
注意,构建的图可以是非连通的。
**输入输出数据格式:**
**输入格式:**
输入由多个测试案例组成。第一行包含一个整数t(1≤t≤10^4)——测试案例的数量。接下来是每个测试案例的描述。
每个测试案例的第一行包含一个整数n(2≤n≤2×10^5)——顶点的数量。
每个测试案例的第二行包含n个整数a_1, a_2, …, a_n(1≤a_i≤10^6)——每个顶点的高度。
保证所有测试案例的n之和不超过2×10^5。
**输出格式:**
对于每个测试案例,输出图中可能的最大边数。**题目大意:** 多雷米的新城市正在建设中!该城市可以被视为一个具有n个顶点的简单无向图。第i个顶点的高度为a_i。现在多雷米正在决定哪些顶点对应该用边连接。 由于经济原因,图中不应有自环或多重边。 出于安全原因,不应存在三个互不相同的顶点u、v和w,使得a_u ≤ a_v ≤ a_w,并且边(u,v)和(v,w)都存在。 在这些约束条件下,多雷米想知道图中可能的最大边数。你能帮她吗? 注意,构建的图可以是非连通的。 **输入输出数据格式:** **输入格式:** 输入由多个测试案例组成。第一行包含一个整数t(1≤t≤10^4)——测试案例的数量。接下来是每个测试案例的描述。 每个测试案例的第一行包含一个整数n(2≤n≤2×10^5)——顶点的数量。 每个测试案例的第二行包含n个整数a_1, a_2, …, a_n(1≤a_i≤10^6)——每个顶点的高度。 保证所有测试案例的n之和不超过2×10^5。 **输出格式:** 对于每个测试案例,输出图中可能的最大边数。