309957: CF1764H. Doremy's Paint 2
Memory Limit:256 MB
Time Limit:4 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Doremy's Paint 2
题意翻译
给定一个长度为 $n$ 的序列 $a_{1\cdots n}$,初始有 $a_i=i$。 现在有 $m$ 个操作,第 $i$ 个操作有参数 $l_i,r_i(l_i\le r_i)$,执行该操作会把 $a_{l_i+1\cdots r_i}$ 赋值为 $a_l$。 给定 $k$,对于所有 $x=1\sim m$,求如果依次执行第 $x$ 个到第 $x+k-1$ 个操作那么序列中有多少种不同的元素。这里将第 $i+m$ 个操作视为第 $i$ 个操作。题目描述
Doremy has $ n $ buckets of paint which is represented by an array $ a $ of length $ n $ . Bucket $ i $ contains paint with color $ a_i $ . Initially, $ a_i=i $ . Doremy has $ m $ segments $ [l_i,r_i] $ ( $ 1 \le l_i \le r_i \le n $ ). Each segment describes an operation. Operation $ i $ is performed as follows: - For each $ j $ such that $ l_i < j \leq r_i $ , set $ a_j := a_{l_i} $ . Doremy also selects an integer $ k $ . She wants to know for each integer $ x $ from $ 0 $ to $ m-1 $ , the number of distinct colors in the array after performing operations $ x \bmod m +1, (x+1) \bmod m + 1, \ldots, (x+k-1) \bmod m +1 $ . Can you help her calculate these values? Note that for each $ x $ individually we start from the initial array and perform only the given $ k $ operations in the given order.输入输出格式
输入格式
The first line of input contains three integers $ n $ , $ m $ , and $ k $ ( $ 1\le n,m\le 2\cdot 10^5 $ , $ 1 \le k \le m $ ) — the length of the array $ a $ , the total number of operations, and the integer that Doremy selects. The $ i $ -th line of the following $ m $ lines contains two integers $ l_i $ , $ r_i $ ( $ 1\le l_i\le r_i\le n $ ) — the bounds of the $ i $ -th segment.
输出格式
Output $ m $ integers. The $ (x+1) $ -th integer should be the number of distinct colors in the array if we start from the initial array and perform operations $ x \bmod m +1, (x+1) \bmod m + 1, \ldots, (x+k-1) \bmod m +1 $ .
输入输出样例
输入样例 #1
7 5 5
3 5
2 3
4 6
5 7
1 2输出样例 #1
3 3 3 3 2输入样例 #2
10 9 4
1 1
2 3
3 4
7 9
6 8
5 7
2 4
9 10
1 3输出样例 #2
6 6 7 6 5 5 7 7 7说明
In the first test case, the picture below shows the resulting array for the values of $ x=0,1,2 $ respectively. 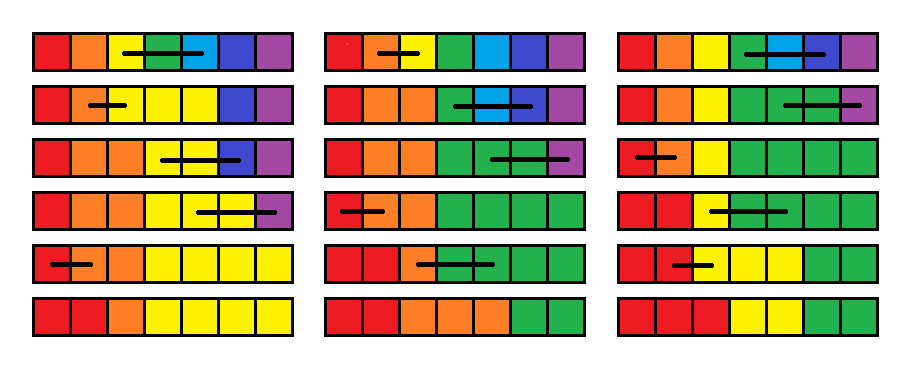Input
题意翻译
给定一个长度为 $n$ 的序列 $a_{1\cdots n}$,初始有 $a_i=i$。 现在有 $m$ 个操作,第 $i$ 个操作有参数 $l_i,r_i(l_i\le r_i)$,执行该操作会把 $a_{l_i+1\cdots r_i}$ 赋值为 $a_l$。 给定 $k$,对于所有 $x=1\sim m$,求如果依次执行第 $x$ 个到第 $x+k-1$ 个操作那么序列中有多少种不同的元素。这里将第 $i+m$ 个操作视为第 $i$ 个操作。Output
**题目大意:**
多瑞米有一个长度为 $ n $ 的颜料桶序列 $ a $,第 $ i $ 个桶初始装有颜色 $ i $ 的颜料。现在有 $ m $ 个操作,每个操作由一对参数 $ l_i, r_i $ 定义($ l_i \le r_i $),执行该操作会将 $ a_{l_i+1} \cdots a_{r_i} $ 的值赋为 $ a_{l_i} $。给定整数 $ k $,需要计算对于每个 $ x = 0 \sim m-1 $,从初始序列开始,依次执行操作 $ x \bmod m + 1, (x+1) \bmod m + 1, \ldots, (x+k-1) \bmod m + 1 $ 后,序列中有多少种不同的颜色。
**输入格式:**
第一行包含三个整数 $ n $, $ m $, 和 $ k $($ 1 \le n, m \le 2 \times 10^5 $,$ 1 \le k \le m $)——序列 $ a $ 的长度、操作的总数和多瑞米选择的整数。
接下来的 $ m $ 行,每行包含两个整数 $ l_i $, $ r_i $($ 1 \le l_i \le r_i \le n $)——第 $ i $ 个操作的界限。
**输出格式:**
输出 $ m $ 个整数。第 $ (x+1) $ 个整数应该是从初始序列开始,执行操作 $ x \bmod m + 1, (x+1) \bmod m + 1, \ldots, (x+k-1) \bmod m + 1 $ 后,序列中不同颜色的数量。**题目大意:** 多瑞米有一个长度为 $ n $ 的颜料桶序列 $ a $,第 $ i $ 个桶初始装有颜色 $ i $ 的颜料。现在有 $ m $ 个操作,每个操作由一对参数 $ l_i, r_i $ 定义($ l_i \le r_i $),执行该操作会将 $ a_{l_i+1} \cdots a_{r_i} $ 的值赋为 $ a_{l_i} $。给定整数 $ k $,需要计算对于每个 $ x = 0 \sim m-1 $,从初始序列开始,依次执行操作 $ x \bmod m + 1, (x+1) \bmod m + 1, \ldots, (x+k-1) \bmod m + 1 $ 后,序列中有多少种不同的颜色。 **输入格式:** 第一行包含三个整数 $ n $, $ m $, 和 $ k $($ 1 \le n, m \le 2 \times 10^5 $,$ 1 \le k \le m $)——序列 $ a $ 的长度、操作的总数和多瑞米选择的整数。 接下来的 $ m $ 行,每行包含两个整数 $ l_i $, $ r_i $($ 1 \le l_i \le r_i \le n $)——第 $ i $ 个操作的界限。 **输出格式:** 输出 $ m $ 个整数。第 $ (x+1) $ 个整数应该是从初始序列开始,执行操作 $ x \bmod m + 1, (x+1) \bmod m + 1, \ldots, (x+k-1) \bmod m + 1 $ 后,序列中不同颜色的数量。
多瑞米有一个长度为 $ n $ 的颜料桶序列 $ a $,第 $ i $ 个桶初始装有颜色 $ i $ 的颜料。现在有 $ m $ 个操作,每个操作由一对参数 $ l_i, r_i $ 定义($ l_i \le r_i $),执行该操作会将 $ a_{l_i+1} \cdots a_{r_i} $ 的值赋为 $ a_{l_i} $。给定整数 $ k $,需要计算对于每个 $ x = 0 \sim m-1 $,从初始序列开始,依次执行操作 $ x \bmod m + 1, (x+1) \bmod m + 1, \ldots, (x+k-1) \bmod m + 1 $ 后,序列中有多少种不同的颜色。
**输入格式:**
第一行包含三个整数 $ n $, $ m $, 和 $ k $($ 1 \le n, m \le 2 \times 10^5 $,$ 1 \le k \le m $)——序列 $ a $ 的长度、操作的总数和多瑞米选择的整数。
接下来的 $ m $ 行,每行包含两个整数 $ l_i $, $ r_i $($ 1 \le l_i \le r_i \le n $)——第 $ i $ 个操作的界限。
**输出格式:**
输出 $ m $ 个整数。第 $ (x+1) $ 个整数应该是从初始序列开始,执行操作 $ x \bmod m + 1, (x+1) \bmod m + 1, \ldots, (x+k-1) \bmod m + 1 $ 后,序列中不同颜色的数量。**题目大意:** 多瑞米有一个长度为 $ n $ 的颜料桶序列 $ a $,第 $ i $ 个桶初始装有颜色 $ i $ 的颜料。现在有 $ m $ 个操作,每个操作由一对参数 $ l_i, r_i $ 定义($ l_i \le r_i $),执行该操作会将 $ a_{l_i+1} \cdots a_{r_i} $ 的值赋为 $ a_{l_i} $。给定整数 $ k $,需要计算对于每个 $ x = 0 \sim m-1 $,从初始序列开始,依次执行操作 $ x \bmod m + 1, (x+1) \bmod m + 1, \ldots, (x+k-1) \bmod m + 1 $ 后,序列中有多少种不同的颜色。 **输入格式:** 第一行包含三个整数 $ n $, $ m $, 和 $ k $($ 1 \le n, m \le 2 \times 10^5 $,$ 1 \le k \le m $)——序列 $ a $ 的长度、操作的总数和多瑞米选择的整数。 接下来的 $ m $ 行,每行包含两个整数 $ l_i $, $ r_i $($ 1 \le l_i \le r_i \le n $)——第 $ i $ 个操作的界限。 **输出格式:** 输出 $ m $ 个整数。第 $ (x+1) $ 个整数应该是从初始序列开始,执行操作 $ x \bmod m + 1, (x+1) \bmod m + 1, \ldots, (x+k-1) \bmod m + 1 $ 后,序列中不同颜色的数量。