Koxia and Tree

题意翻译

有一棵 $n$ 个结点的无根树，边从 $1$ 到 $n-1$ 标号，第 $i$ 条边连接结点 $u_i$ 和 $v_i$。 有 $k$ 个结点带有标记，分别是 $a_1,a_2,\cdots,a_k$（$\forall i\not= j,a_i\not = a_j$）。接下来，进行如下操作： 1. 给每条边随机定向。 2. **按照编号顺序**，对于每一条边 $u\to v$，如果结点 $u$ 有标记而 $v$ 没有，那么就把 $u$ 的标记转移到 $v$ 上。 3. 随机选取两个不同的标记点，计算它们的距离。 你需要给出第三步中距离的期望值。对 998244353 取模。

题目描述

Imi has an undirected tree with $ n $ vertices where edges are numbered from $ 1 $ to $ n-1 $ . The $ i $ -th edge connects vertices $ u_i $ and $ v_i $ . There are also $ k $ butterflies on the tree. Initially, the $ i $ -th butterfly is on vertex $ a_i $ . All values of $ a $ are pairwise distinct. Koxia plays a game as follows: - For $ i = 1, 2, \dots, n - 1 $ , Koxia set the direction of the $ i $ -th edge as $ u_i \rightarrow v_i $ or $ v_i \rightarrow u_i $ with equal probability. - For $ i = 1, 2, \dots, n - 1 $ , if a butterfly is on the initial vertex of $ i $ -th edge and there is no butterfly on the terminal vertex, then this butterfly flies to the terminal vertex. Note that operations are sequentially in order of $ 1, 2, \dots, n - 1 $ instead of simultaneously. - Koxia chooses two butterflies from the $ k $ butterflies with equal probability from all possible $ \frac{k(k-1)}{2} $ ways to select two butterflies, then she takes the distance $ ^\dagger $ between the two chosen vertices as her score. Now, Koxia wants you to find the expected value of her score, modulo $ 998\,244\,353^\ddagger $ . $ ^\dagger $ The distance between two vertices on a tree is the number of edges on the (unique) simple path between them. $ ^\ddagger $ Formally, let $ M = 998\,244\,353 $ . It can be shown that the answer can be expressed as an irreducible fraction $ \frac{p}{q} $ , where $ p $ and $ q $ are integers and $ q \not \equiv 0 \pmod{M} $ . Output the integer equal to $ p \cdot q^{-1} \bmod M $ . In other words, output such an integer $ x $ that $ 0 \le x < M $ and $ x \cdot q \equiv p \pmod{M} $ .

输入输出格式

输入格式

The first line contains two integers $ n $ , $ k $ ( $ 2 \leq k \leq n \leq 3 \cdot {10}^5 $ ) — the size of the tree and the number of butterflies. The second line contains $ k $ integers $ a_1, a_2, \dots, a_k $ ( $ 1 \leq a_i \leq n $ ) — the initial position of butterflies. It's guaranteed that all positions are distinct. The $ i $ -th line in following $ n − 1 $ lines contains two integers $ u_i $ , $ v_i $ ( $ 1 \leq u_i, v_i \leq n $ , $ u_i \neq v_i $ ) — the vertices the $ i $ -th edge connects. It is guaranteed that the given edges form a tree.

输出格式

Output a single integer — the expected value of Koxia's score, modulo $ 998\,244\,353 $ .

输入输出样例

输入样例 #1

3 2
1 3
1 2
2 3

输出样例 #1

748683266

输入样例 #2

5 3
3 4 5
1 2
1 3
2 4
2 5

输出样例 #2

831870296

说明

In the first test case, the tree is shown below. Vertices containing butterflies are noted as bold. 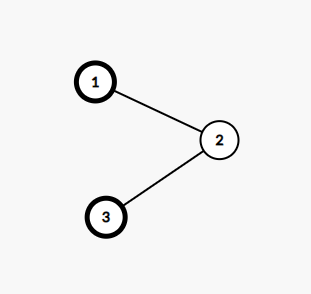There are only $ 2 $ butterflies so the choice of butterflies is fixed. Let's consider the following $ 4 $ cases: - Edges are $ 1 \rightarrow 2 $ and $ 2 \rightarrow 3 $ : butterfly on vertex $ 1 $ moves to vertex $ 2 $ , but butterfly on vertex $ 3 $ doesn't move. The distance between vertices $ 2 $ and $ 3 $ is $ 1 $ . - Edges are $ 1 \rightarrow 2 $ and $ 3 \rightarrow 2 $ : butterfly on vertex $ 1 $ moves to vertex $ 2 $ , but butterfly on vertex $ 3 $ can't move to vertex $ 2 $ because it's occupied. The distance between vertices $ 2 $ and $ 3 $ is $ 1 $ . - Edges are $ 2 \rightarrow 1 $ and $ 2 \rightarrow 3 $ : butterflies on both vertex $ 1 $ and vertex $ 3 $ don't move. The distance between vertices $ 1 $ and $ 3 $ is $ 2 $ . - Edges are $ 2 \rightarrow 1 $ and $ 3 \rightarrow 2 $ : butterfly on vertex $ 1 $ doesn't move, but butterfly on vertex $ 3 $ move to vertex $ 2 $ . The distance between vertices $ 1 $ and $ 2 $ is $ 1 $ . Therefore, the expected value of Koxia's score is $ \frac {1+1+2+1} {4} = \frac {5} {4} $ , which is $ 748\,683\,266 $ after modulo $ 998\,244\,353 $ . In the second test case, the tree is shown below. Vertices containing butterflies are noted as bold. The expected value of Koxia's score is $ \frac {11} {6} $ , which is $ 831\,870\,296 $ after modulo $ 998\,244\,353 $ . 

**题目大意：**
有一棵有 $ n $ 个节点的无根树，边从 $ 1 $ 到 $ n-1 $ 编号，第 $ i $ 条边连接节点 $ u_i $ 和 $ v_i $。有 $ k $ 个节点带有标记，分别是 $ a_1, a_2, \cdots, a_k $（对于所有 $ i \not= j $，有 $ a_i \not= a_j $）。接下来，进行如下操作：

1. 随机给每条边定向。
2. **按照编号顺序**，对于每一条边 $ u \to v $，如果节点 $ u $ 有标记而 $ v $ 没有，那么就把 $ u $ 的标记转移到 $ v $ 上。
3. 随机选取两个不同的标记点，计算它们的距离。

需要计算第三步中距离的期望值。结果对 $ 998244353 $ 取模。

**输入输出数据格式：**

**输入格式：**
- 第一行包含两个整数 $ n $, $ k $（$ 2 \leq k \leq n \leq 3 \cdot 10^5 $）——树的大小和蝴蝶的数量。
- 第二行包含 $ k $ 个整数 $ a_1, a_2, \dots, a_k $（$ 1 \leq a_i \leq n $）——蝴蝶的初始位置。保证所有位置都不同。
- 接下来的 $ n-1 $ 行中，每行包含两个整数 $ u_i $, $ v_i $（$ 1 \leq u_i, v_i \leq n $，$ u_i \neq v_i $）——第 $ i $ 条边连接的节点。保证给定的边构成一棵树。

**输出格式：**
- 输出一个整数——Koxia得分的期望值，对 $ 998244353 $ 取模。

**输入输出样例：**

**输入样例 #1**
```
3 2
1 3
1 2
2 3
```
**输出样例 #1**
```
748683266
```

**输入样例 #2**
```
5 3
3 4 5
1 2
1 3
2 4
2 5
```
**输出样例 #2**
```
831870296
```

**说明：**
在第一个测试案例中，树如下所示。带有蝴蝶的节点用粗体标记。由于只有 $ 2 $ 只蝴蝶，所以选择蝴蝶的方式是固定的。考虑以下 $ 4 $ 种情况：

- 边是 $ 1 \rightarrow 2 $ 和 $ 2 \rightarrow 3 $：节点 $ 1 $ 上的蝴蝶移动到节点 $ 2 $，但节点 $ 3 $ 上的蝴蝶不动。节点 $ 2 $ 和 $ 3 $ 之间的距离是 $ 1 $。
- 边是 $ 1 \rightarrow 2 $ 和 $ 3 \rightarrow 2 $：节点 $ 1 $ 上的蝴蝶移动到节点 $ 2 $，但节点 $ 3 $ 上的蝴蝶不能移动到节点 $ 2 $ 因为它被占领了。节点 $ 2 $ 和 $ 3 $ 之间的距离是 $ 1 $。
- 边是 $ 2 \rightarrow 1 $ 和 $ 2 \rightarrow 3 $：节点 $ 1 $ 和节点 $ 3 $ 上的蝴蝶都不动。节点 $ 1 $ 和 $ 3 $ 之间的距离是 $ 2 $。
- 边是 $ 2 \rightarrow 1 $ 和 $ 3 \rightarrow 2 $：节点 $ 1 $ 上的蝴蝶不动，但节点 $ 3 $ 上的蝴蝶移动到节点 $ 2 $。节点 $ 1 $ 和 $ 2 $ 之间的距离是 $ 1 $。

因此，Koxia得分的期望值是 $ \frac {1+1+2+1} {4} = \frac {5} {4} $，模 $ 998244353 $ 后是 $ 748683266 $。

在第二个测试案例中，树如下所示。带有蝴蝶的节点用粗体标记。Koxia得分的期望值是 $ \frac {11} {6} $，模 $ 998244353 $ 后是 $ 831870296 $。**题目大意：** 有一棵有 $ n $ 个节点的无根树，边从 $ 1 $ 到 $ n-1 $ 编号，第 $ i $ 条边连接节点 $ u_i $ 和 $ v_i $。有 $ k $ 个节点带有标记，分别是 $ a_1, a_2, \cdots, a_k $（对于所有 $ i \not= j $，有 $ a_i \not= a_j $）。接下来，进行如下操作： 1. 随机给每条边定向。 2. **按照编号顺序**，对于每一条边 $ u \to v $，如果节点 $ u $ 有标记而 $ v $ 没有，那么就把 $ u $ 的标记转移到 $ v $ 上。 3. 随机选取两个不同的标记点，计算它们的距离。 需要计算第三步中距离的期望值。结果对 $ 998244353 $ 取模。 **输入输出数据格式：** **输入格式：** - 第一行包含两个整数 $ n $, $ k $（$ 2 \leq k \leq n \leq 3 \cdot 10^5 $）——树的大小和蝴蝶的数量。 - 第二行包含 $ k $ 个整数 $ a_1, a_2, \dots, a_k $（$ 1 \leq a_i \leq n $）——蝴蝶的初始位置。保证所有位置都不同。 - 接下来的 $ n-1 $ 行中，每行包含两个整数 $ u_i $, $ v_i $（$ 1 \leq u_i, v_i \leq n $，$ u_i \neq v_i $）——第 $ i $ 条边连接的节点。保证给定的边构成一棵树。 **输出格式：** - 输出一个整数——Koxia得分的期望值，对 $ 998244353 $ 取模。 **输入输出样例：** **输入样例 #1** ``` 3 2 1 3 1 2 2 3 ``` **输出样例 #1** ``` 748683266 ``` **输入样例 #2** ``` 5 3 3 4 5 1 2 1 3 2 4 2 5 ``` **输出样例 #2** ``` 831870296 ``` **说明：** 在第一个测试案例中，树如下所示。带有蝴蝶的节点用粗体标记。由于只有 $ 2 $ 只蝴蝶，所以选择蝴蝶的方式是固定的。考虑以下 $ 4 $ 种情况： - 边是 $ 1 \rightarrow 2 $ 和 $ 2 \rightarrow 3 $：节点 $ 1 $ 上的蝴蝶移动到节点 $ 2 $，但节点 $ 3 $ 上的蝴蝶不动。节点 $ 2 $ 和 $ 3 $ 之间的距离是 $ 1 $。 - 边是 $ 1 \rightarrow 2 $ 和 $ 3 \rightarrow 2 $：节点 $ 1 $ 上的蝴蝶移动到节点 $ 2 $，但节点 $ 3 $ 上的蝴蝶不能移动到节点 $ 2 $ 因为它被占领了。节点 $ 2 $ 和 $ 3 $ 之间的距离是 $ 1 $。 - 边是 $ 2 \rightarrow 1 $ 和 $ 2 \rightarrow 3 $：节点 $ 1 $ 和节点 $ 3 $ 上的蝴蝶都不动。节点 $ 1 $ 和 $ 3 $ 之间的距离是 $ 2 $。 - 边是 $ 2 \rightarrow 1 $ 和 $ 3 \rightarrow 2 $：节点 $ 1 $ 上的蝴蝶不动，但节点 $ 3 $ 上的蝴蝶移动到节点 $ 2 $。节点 $ 1 $ 和 $ 2 $ 之间的距离是 $ 1 $。 因此，Koxia得分的期望值是 $ \frac {1+1+2+1} {4} = \frac {5} {4} $，模 $ 998244353 $ 后是 $ 748683266 $。 在第二个测试案例中，树如下所示。带有蝴蝶的节点用粗体标记。Koxia得分的期望值是 $ \frac {11} {6} $，模 $ 998244353 $ 后是 $ 831870296 $。