Hossam and (sub-)palindromic tree

题意翻译

给定一棵 $n$ 个结点的树，每个结点上有一个字符。求树上所有点对之间路径组成的字符串的最长回文**子序列**的长度。

题目描述

Hossam has an unweighted tree $ G $ with letters in vertices. Hossam defines $ s(v, \, u) $ as a string that is obtained by writing down all the letters on the unique simple path from the vertex $ v $ to the vertex $ u $ in the tree $ G $ . A string $ a $ is a subsequence of a string $ s $ if $ a $ can be obtained from $ s $ by deletion of several (possibly, zero) letters. For example, "dores", "cf", and "for" are subsequences of "codeforces", while "decor" and "fork" are not. A palindrome is a string that reads the same from left to right and from right to left. For example, "abacaba" is a palindrome, but "abac" is not. Hossam defines a sub-palindrome of a string $ s $ as a subsequence of $ s $ , that is a palindrome. For example, "k", "abba" and "abhba" are sub-palindromes of the string "abhbka", but "abka" and "cat" are not. Hossam defines a maximal sub-palindrome of a string $ s $ as a sub-palindrome of $ s $ , which has the maximal length among all sub-palindromes of $ s $ . For example, "abhbka" has only one maximal sub-palindrome — "abhba". But it may also be that the string has several maximum sub-palindromes: the string "abcd" has $ 4 $ maximum sub-palindromes. Help Hossam find the length of the longest maximal sub-palindrome among all $ s(v, \, u) $ in the tree $ G $ . Note that the sub-palindrome is a subsequence, not a substring.

输入输出格式

输入格式

The first line contains one integer $ t $ ( $ 1 \le t \le 200 $ ) — the number of test cases. The first line of each test case has one integer number $ n $ ( $ 1 \le n \le 2 \cdot 10^3 $ ) — the number of vertices in the graph. The second line contains a string $ s $ of length $ n $ , the $ i $ -th symbol of which denotes the letter on the vertex $ i $ . It is guaranteed that all characters in this string are lowercase English letters. The next $ n - 1 $ lines describe the edges of the tree. Each edge is given by two integers $ v $ and $ u $ ( $ 1 \le v, \, u \le n $ , $ v \neq u $ ). These two numbers mean that there is an edge $ (v, \, u) $ in the tree. It is guaranteed that the given edges form a tree. It is guaranteed that sum of all $ n $ doesn't exceed $ 2 \cdot 10^3 $ .

输出格式

For each test case output one integer — the length of the longest maximal sub-palindrome among all $ s(v, \, u) $ .

输入输出样例

输入样例 #1

2
5
abaca
1 2
1 3
3 4
4 5
9
caabadedb
1 2
2 3
2 4
1 5
5 6
5 7
5 8
8 9

输出样例 #1

3
5

说明

In the first example the maximal subpalindromes are "aaa" with letters in vertices $ 1, \, 3, \, 5 $ , or "aca" with letters in vertices $ 1, \, 4, \, 5 $ . 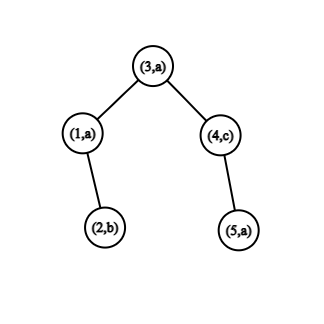 The tree from the first example.In the second example there is only one maximal palindrome "bacab" with letters in vertices $ 4, \, 2, \, 1, \, 5, \, 9 $ . 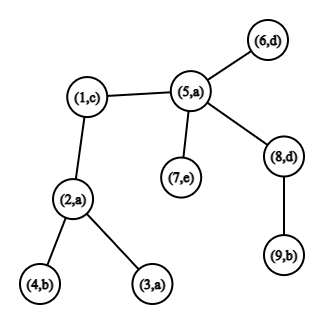 The tree from the second example.

**题意翻译**
给定一棵有 $ n $ 个结点的树，每个结点上有一个字符。求树上所有点对之间路径组成的字符串的最长回文**子序列**的长度。

**题目描述**
Hossam有一棵无权树 $ G $ ，其顶点上写有字母。

Hossam定义 $ s(v, \, u) $ 为在树 $ G $ 中从顶点 $ v $ 到顶点 $ u $ 的唯一简单路径上写下的所有字母组成的字符串。

字符串 $ a $ 是字符串 $ s $ 的子序列，如果 $ a $ 可以通过删除 $ s $ 中的几个（可能为零）字母获得。例如，"dores"、"cf" 和 "for" 都是 "codeforces" 的子序列，而 "decor" 和 "fork" 不是。

回文是指从左到右和从右到左读都相同的字符串。例如，"abacaba" 是回文，但 "abac" 不是。

Hossam定义字符串 $ s $ 的子回文为 $ s $ 的一个回文子序列。例如，"k"、"abba" 和 "abhba" 都是字符串 "abhbka" 的子回文，但 "abka" 和 "cat" 不是。

Hossam定义字符串 $ s $ 的最大子回文为 $ s $ 的具有所有子回文中最长长度的子回文。例如，"abhbka" 只有一个最大子回文——"abhba"。但也可能字符串有多个最大子回文：字符串 "abcd" 有 4 个最大子回文。

帮助Hossam找到树上所有 $ s(v, \, u) $ 中最长的最大子回文的长度。

注意子回文是一个子序列，而不是子串。

**输入输出格式**
**输入格式**
第一行包含一个整数 $ t $ ( $ 1 \le t \le 200 $ ) —— 测试用例的数量。

每个测试用例的第一行有一个整数 $ n $ ( $ 1 \le n \le 2 \cdot 10^3 $ ) —— 图中的顶点数。

第二行包含一个长度为 $ n $ 的字符串 $ s $ ，其中第 $ i $ 个符号表示顶点 $ i $ 上的字母。保证这个字符串中的所有字符都是小写英文字母。

接下来的 $ n - 1 $ 行描述树的边。每条边由两个整数 $ v $ 和 $ u $ ( $ 1 \le v, \, u \le n $ , $ v \neq u $ ) 给出。这两个数字表示在树中有一条边 $ (v, \, u) $ 。保证给定的边构成一棵树。

保证所有 $ n $ 的和不超过 $ 2 \cdot 10^3 $ 。

**输出格式**
对于每个测试用例输出一个整数——所有 $ s(v, \, u) $ 中最长的最大子回文的长度。

**输入输出样例**
**输入样例 #1**
```
2
5
abaca
1 2
1 3
3 4
4 5
9
caabadedb
1 2
2 3
2 4
1 5
5 6
5 7
5 8
8 9
```
**输出样例 #1**
```
3
5
```**题意翻译** 给定一棵有 $ n $ 个结点的树，每个结点上有一个字符。求树上所有点对之间路径组成的字符串的最长回文**子序列**的长度。 **题目描述** Hossam有一棵无权树 $ G $ ，其顶点上写有字母。 Hossam定义 $ s(v, \, u) $ 为在树 $ G $ 中从顶点 $ v $ 到顶点 $ u $ 的唯一简单路径上写下的所有字母组成的字符串。 字符串 $ a $ 是字符串 $ s $ 的子序列，如果 $ a $ 可以通过删除 $ s $ 中的几个（可能为零）字母获得。例如，"dores"、"cf" 和 "for" 都是 "codeforces" 的子序列，而 "decor" 和 "fork" 不是。 回文是指从左到右和从右到左读都相同的字符串。例如，"abacaba" 是回文，但 "abac" 不是。 Hossam定义字符串 $ s $ 的子回文为 $ s $ 的一个回文子序列。例如，"k"、"abba" 和 "abhba" 都是字符串 "abhbka" 的子回文，但 "abka" 和 "cat" 不是。 Hossam定义字符串 $ s $ 的最大子回文为 $ s $ 的具有所有子回文中最长长度的子回文。例如，"abhbka" 只有一个最大子回文——"abhba"。但也可能字符串有多个最大子回文：字符串 "abcd" 有 4 个最大子回文。 帮助Hossam找到树上所有 $ s(v, \, u) $ 中最长的最大子回文的长度。 注意子回文是一个子序列，而不是子串。 **输入输出格式** **输入格式** 第一行包含一个整数 $ t $ ( $ 1 \le t \le 200 $ ) —— 测试用例的数量。 每个测试用例的第一行有一个整数 $ n $ ( $ 1 \le n \le 2 \cdot 10^3 $ ) —— 图中的顶点数。 第二行包含一个长度为 $ n $ 的字符串 $ s $ ，其中第 $ i $ 个符号表示顶点 $ i $ 上的字母。保证这个字符串中的所有字符都是小写英文字母。 接下来的 $ n - 1 $ 行描述树的边。每条边由两个整数 $ v $ 和 $ u $ ( $ 1 \le v, \, u \le n $ , $ v \neq u $ ) 给出。这两个数字表示在树中有一条边 $ (v, \, u) $ 。保证给定的边构成一棵树。 保证所有 $ n $ 的和不超过 $ 2 \cdot 10^3 $ 。 **输出格式** 对于每个测试用例输出一个整数——所有 $ s(v, \, u) $ 中最长的最大子回文的长度。 **输入输出样例** **输入样例 #1** ``` 2 5 abaca 1 2 1 3 3 4 4 5 9 caabadedb 1 2 2 3 2 4 1 5 5 6 5 7 5 8 8 9 ``` **输出样例 #1** ``` 3 5 ```