310052: CF1776F. Train Splitting
Memory Limit:256 MB
Time Limit:2 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Train Splitting
题意翻译
有一个 $n$ 点 $m$ 边简单无向连通图,请用若干(至少为 $2$)种颜色对每条边染色,使得: - 对于每种颜色,仅由该颜色的边组成的生成子图不连通。 - 对于每两种颜色,仅由该颜色的边组成的生成子图连通。题目描述
There are $ n $ big cities in Italy, and there are $ m $ train routes between pairs of cities. Each route connects two different cities bidirectionally. Moreover, using the trains one can reach every city starting from any other city. Right now, all the routes are operated by the government-owned Italian Carriage Passenger Company, but the government wants to privatize the routes. The government does not want to give too much power to a single company, but it also does not want to make people buy a lot of different subscriptions. Also, it would like to give a fair chance to all companies. In order to formalize all these wishes, the following model was proposed. There will be $ k \ge 2 $ private companies indexed by $ 1, \, 2, \, \dots, \, k $ . Each train route will be operated by exactly one of the $ k $ companies. Then: - For any company, there should exist two cities such that it is impossible to reach one from the other using only routes operated by that company. - On the other hand, for any two companies, it should be possible to reach every city from any other city using only routes operated by these two companies. Find a plan satisfying all these criteria. It can be shown that a viable plan always exists. Please note that you can choose the number $ k $ and you do not have to minimize or maximize it.输入输出格式
输入格式
Each test contains multiple test cases. The first line contains an integer $ t $ ( $ 1 \le t \le 1000 $ ) — the number of test cases. The descriptions of the $ t $ test cases follow. The first line of each test case contains two integers $ n $ and $ m $ ( $ 3 \le n \le 50 $ , $ n-1 \le m \le n(n-1)/2 $ ) — the number of cities and the number of train routes. The next $ m $ lines contain two integers $ u_i $ and $ v_i $ each ( $ 1 \le u_i, v_i \le n $ , $ u_i \ne v_i $ ) — the $ i $ -th train route connects cities $ u_i $ and $ v_i $ . It is guaranteed that the routes connect $ m $ distinct pairs of cities. It is guaranteed that using the trains one can reach every city starting from any other city. The sum of the values of $ n $ over all test cases does not exceed $ 5000 $ .
输出格式
For each test case, on the first line print an integer $ k $ ( $ 2 \le k \le m $ ) — the number of companies in your plan; on the second line print $ m $ integers $ c_1, \, c_2, \, \dots, \, c_m $ ( $ 1 \le c_i \le k $ ) — in your plan company $ c_i $ operates the $ i $ -th route. If there are multiple valid plans, you may print any of them.
输入输出样例
输入样例 #1
2
5 9
1 2
1 3
1 4
1 5
2 3
2 4
2 5
3 4
3 5
3 3
1 2
3 1
2 3输出样例 #1
4
1 2 3 1 4 2 2 4 3
3
2 3 1说明
In the first test case, the output is illustrated in the following picture, where different colors correspond to different companies (blue for $ 1 $ , red for $ 2 $ , green for $ 3 $ , and yellow for $ 4 $ ): 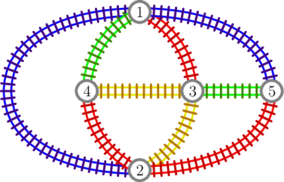If we consider, for example, only companies $ 2 $ and $ 3 $ , we can see that from any city it is possible to reach every other city (picture on the left below). However, if we restrict to company $ 2 $ alone, it becomes impossible to reach city $ 5 $ from city $ 1 $ (picture on the right). 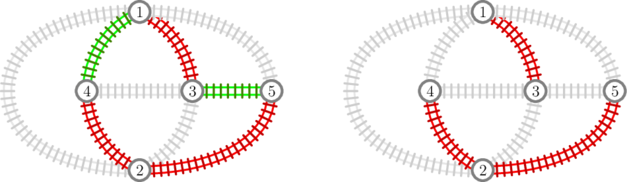In the second test case, the output is illustrated in the following picture: 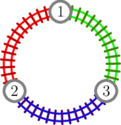Input
题意翻译
有一个 $n$ 点 $m$ 边简单无向连通图,请用若干(至少为 $2$)种颜色对每条边染色,使得: - 对于每种颜色,仅由该颜色的边组成的生成子图不连通。 - 对于每两种颜色,仅由该颜色的边组成的生成子图连通。Output
题目大意:
有一个包含n个点、m条边的简单无向连通图,要用至少2种颜色对每条边进行染色,满足以下条件:
- 对于任意一种颜色,仅由该颜色的边组成的生成子图不连通。
- 对于任意两种颜色,仅由这两种颜色的边组成的生成子图是连通的。
输入输出数据格式:
输入:
- 第一行包含一个整数t(1≤t≤1000),表示测试用例的数量。
- 每个测试用例的第一行包含两个整数n和m(3≤n≤50,n-1≤m≤n(n-1)/2),分别表示城市的数量和火车路线的数量。
- 接下来的m行,每行包含两个整数u_i和v_i(1≤u_i,v_i≤n,u_i≠v_i),表示第i条火车路线连接的城市。
输出:
- 对于每个测试用例,第一行输出一个整数k(2≤k≤m),表示计划中的公司数量。
- 第二行输出m个整数c_1,c_2,…,c_m(1≤c_i≤k),表示在你的计划中,第i条路线由公司c_i运营。
输入输出样例:
输入样例 #1:
```
2
5 9
1 2
1 3
1 4
1 5
2 3
2 4
2 5
3 4
3 5
3 3
1 2
3 1
2 3
```
输出样例 #1:
```
4
1 2 3 1 4 2 2 4 3
3
2 3 1
```
说明:
- 在第一个测试用例中,输出用不同颜色表示不同公司(蓝色为1,红色为2,绿色为3,黄色为4)。
- 如果考虑公司2和3,从任何城市都可以到达其他每个城市。但如果只考虑公司2,则无法从城市1到达城市5。
- 第二个测试用例的输出用图表展示。题目大意: 有一个包含n个点、m条边的简单无向连通图,要用至少2种颜色对每条边进行染色,满足以下条件: - 对于任意一种颜色,仅由该颜色的边组成的生成子图不连通。 - 对于任意两种颜色,仅由这两种颜色的边组成的生成子图是连通的。 输入输出数据格式: 输入: - 第一行包含一个整数t(1≤t≤1000),表示测试用例的数量。 - 每个测试用例的第一行包含两个整数n和m(3≤n≤50,n-1≤m≤n(n-1)/2),分别表示城市的数量和火车路线的数量。 - 接下来的m行,每行包含两个整数u_i和v_i(1≤u_i,v_i≤n,u_i≠v_i),表示第i条火车路线连接的城市。 输出: - 对于每个测试用例,第一行输出一个整数k(2≤k≤m),表示计划中的公司数量。 - 第二行输出m个整数c_1,c_2,…,c_m(1≤c_i≤k),表示在你的计划中,第i条路线由公司c_i运营。 输入输出样例: 输入样例 #1: ``` 2 5 9 1 2 1 3 1 4 1 5 2 3 2 4 2 5 3 4 3 5 3 3 1 2 3 1 2 3 ``` 输出样例 #1: ``` 4 1 2 3 1 4 2 2 4 3 3 2 3 1 ``` 说明: - 在第一个测试用例中,输出用不同颜色表示不同公司(蓝色为1,红色为2,绿色为3,黄色为4)。 - 如果考虑公司2和3,从任何城市都可以到达其他每个城市。但如果只考虑公司2,则无法从城市1到达城市5。 - 第二个测试用例的输出用图表展示。
有一个包含n个点、m条边的简单无向连通图,要用至少2种颜色对每条边进行染色,满足以下条件:
- 对于任意一种颜色,仅由该颜色的边组成的生成子图不连通。
- 对于任意两种颜色,仅由这两种颜色的边组成的生成子图是连通的。
输入输出数据格式:
输入:
- 第一行包含一个整数t(1≤t≤1000),表示测试用例的数量。
- 每个测试用例的第一行包含两个整数n和m(3≤n≤50,n-1≤m≤n(n-1)/2),分别表示城市的数量和火车路线的数量。
- 接下来的m行,每行包含两个整数u_i和v_i(1≤u_i,v_i≤n,u_i≠v_i),表示第i条火车路线连接的城市。
输出:
- 对于每个测试用例,第一行输出一个整数k(2≤k≤m),表示计划中的公司数量。
- 第二行输出m个整数c_1,c_2,…,c_m(1≤c_i≤k),表示在你的计划中,第i条路线由公司c_i运营。
输入输出样例:
输入样例 #1:
```
2
5 9
1 2
1 3
1 4
1 5
2 3
2 4
2 5
3 4
3 5
3 3
1 2
3 1
2 3
```
输出样例 #1:
```
4
1 2 3 1 4 2 2 4 3
3
2 3 1
```
说明:
- 在第一个测试用例中,输出用不同颜色表示不同公司(蓝色为1,红色为2,绿色为3,黄色为4)。
- 如果考虑公司2和3,从任何城市都可以到达其他每个城市。但如果只考虑公司2,则无法从城市1到达城市5。
- 第二个测试用例的输出用图表展示。题目大意: 有一个包含n个点、m条边的简单无向连通图,要用至少2种颜色对每条边进行染色,满足以下条件: - 对于任意一种颜色,仅由该颜色的边组成的生成子图不连通。 - 对于任意两种颜色,仅由这两种颜色的边组成的生成子图是连通的。 输入输出数据格式: 输入: - 第一行包含一个整数t(1≤t≤1000),表示测试用例的数量。 - 每个测试用例的第一行包含两个整数n和m(3≤n≤50,n-1≤m≤n(n-1)/2),分别表示城市的数量和火车路线的数量。 - 接下来的m行,每行包含两个整数u_i和v_i(1≤u_i,v_i≤n,u_i≠v_i),表示第i条火车路线连接的城市。 输出: - 对于每个测试用例,第一行输出一个整数k(2≤k≤m),表示计划中的公司数量。 - 第二行输出m个整数c_1,c_2,…,c_m(1≤c_i≤k),表示在你的计划中,第i条路线由公司c_i运营。 输入输出样例: 输入样例 #1: ``` 2 5 9 1 2 1 3 1 4 1 5 2 3 2 4 2 5 3 4 3 5 3 3 1 2 3 1 2 3 ``` 输出样例 #1: ``` 4 1 2 3 1 4 2 2 4 3 3 2 3 1 ``` 说明: - 在第一个测试用例中,输出用不同颜色表示不同公司(蓝色为1,红色为2,绿色为3,黄色为4)。 - 如果考虑公司2和3,从任何城市都可以到达其他每个城市。但如果只考虑公司2,则无法从城市1到达城市5。 - 第二个测试用例的输出用图表展示。