310087: CF1781A. Parallel Projection
Memory Limit:512 MB
Time Limit:1 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Parallel Projection
题意翻译
- **本题一个测试点内有多组测试数据**。 - 在一个三维坐标系中有一个左下角坐标为 $(0,0,0)$,右上角坐标为 $(w,d,h)$ 的每条边都平行于坐标轴的长方体。 - 求从点 $(a,b,0)$ 到点 $(f,g,h)$ 满足以下条件的路线长度最小值: - 行走的每一段路都平行于坐标轴; - 路线应完全在长方体表面,不能离开长方体或进入长方体内部。 - $w,d,h\leq1000$,$0<a,f<w$,$0<b,g<d$。题目描述
Vika's house has a room in a shape of a rectangular parallelepiped (also known as a rectangular cuboid). Its floor is a rectangle of size $ w \times d $ , and the ceiling is right above at the constant height of $ h $ . Let's introduce a coordinate system on the floor so that its corners are at points $ (0, 0) $ , $ (w, 0) $ , $ (w, d) $ , and $ (0, d) $ . A laptop is standing on the floor at point $ (a, b) $ . A projector is hanging on the ceiling right above point $ (f, g) $ . Vika wants to connect the laptop and the projector with a cable in such a way that the cable always goes along the walls, ceiling, or floor (i. e. does not go inside the cuboid). Additionally, the cable should always run parallel to one of the cuboid's edges (i. e. it can not go diagonally). What is the minimum length of a cable that can connect the laptop to the projector? 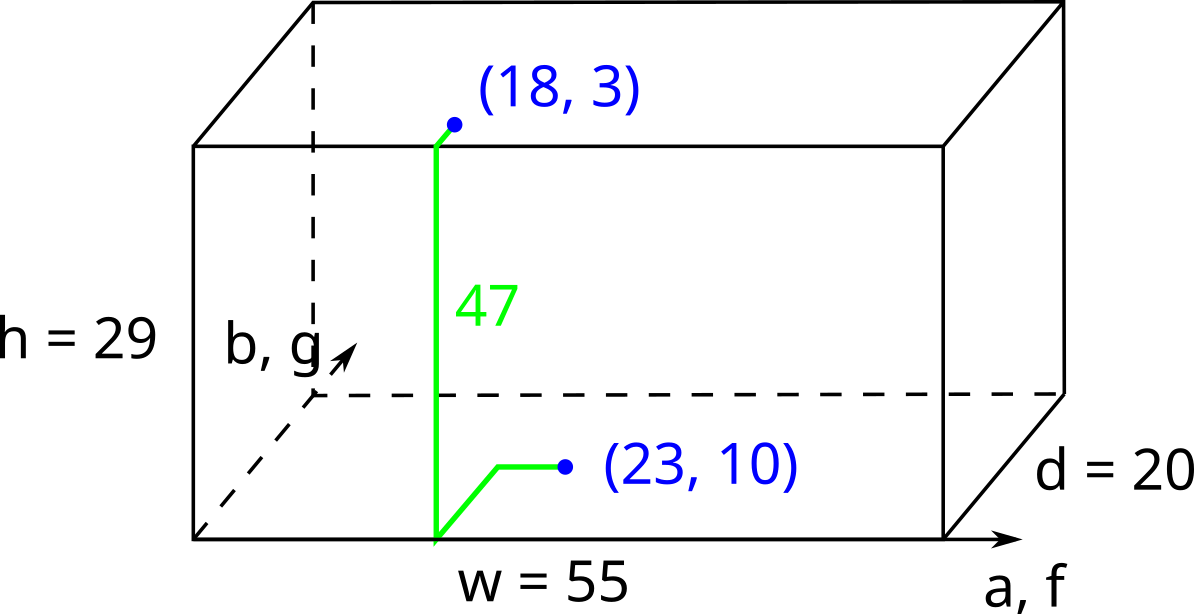 Illustration for the first test case. One of the optimal ways to put the cable is shown in green.输入输出格式
输入格式
Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10^4 $ ). The description of the test cases follows. The first line of each test case contains three integers $ w $ , $ d $ , and $ h $ ( $ 2 \le w, d, h \le 1000 $ ) — the size of the room. The second line contains four integers $ a $ , $ b $ , $ f $ , $ g $ ( $ 0 < a, f < w $ ; $ 0 < b, g < d $ ): the laptop is located on the floor at point $ (a, b) $ , while the projector is hanging on the ceiling right above point $ (f, g) $ .
输出格式
For each test case, print a single integer — the minimum length of the cable connecting the laptop and the projector that runs only along the walls, floor, and ceiling parallel to cuboid's edges.
输入输出样例
输入样例 #1
5
55 20 29
23 10 18 3
20 10 5
1 5 2 5
15 15 4
7 13 10 10
2 1000 2
1 1 1 999
10 4 10
7 1 2 1输出样例 #1
47
8
14
1002
17说明
The picture in the statement illustrates the first test case.Input
题意翻译
- **本题一个测试点内有多组测试数据**。 - 在一个三维坐标系中有一个左下角坐标为 $(0,0,0)$,右上角坐标为 $(w,d,h)$ 的每条边都平行于坐标轴的长方体。 - 求从点 $(a,b,0)$ 到点 $(f,g,h)$ 满足以下条件的路线长度最小值: - 行走的每一段路都平行于坐标轴; - 路线应完全在长方体表面,不能离开长方体或进入长方体内部。 - $w,d,h\leq1000$,$0<a,f<w$,$0<b,g<d$。Output
**平行投影**
**题意翻译**
- **本题一个测试点内有多组测试数据**。
- 在一个三维坐标系中有一个左下角坐标为 $(0,0,0)$,右上角坐标为 $(w,d,h)$ 的每条边都平行于坐标轴的长方体。
- 求从点 $(a,b,0)$ 到点 $(f,g,h)$ 满足以下条件的路线长度最小值:
- 行走的每一段路都平行于坐标轴;
- 路线应完全在长方体表面,不能离开长方体或进入长方体内部。
- $w,d,h\leq1000$,$0
**题目描述**
Vika's house has a room in the shape of a rectangular parallelepiped (also known as a rectangular cuboid). Its floor is a rectangle of size $ w \times d $, and the ceiling is right above at the constant height of $ h $. Let's introduce a coordinate system on the floor so that its corners are at points $ (0, 0) $, $ (w, 0) $, $ (w, d) $, and $ (0, d) $.
A laptop is standing on the floor at point $ (a, b) $. A projector is hanging on the ceiling right above point $ (f, g) $. Vika wants to connect the laptop and the projector with a cable in such a way that the cable always goes along the walls, ceiling, or floor (i.e., does not go inside the cuboid). Additionally, the cable should always run parallel to one of the cuboid's edges (i.e., it can not go diagonally).
What is the minimum length of a cable that can connect the laptop to the projector?
Illustration for the first test case. One of the optimal ways to put the cable is shown in green.
**输入输出格式**
**输入格式**
每个测试包含多个测试案例。第一行包含测试案例的数量 $ t $ ($ 1 \le t \le 10^4 $)。测试案例的描述如下。
每个测试案例的第一行包含三个整数 $ w $, $ d $, 和 $ h $ ($ 2 \le w, d, h \le 1000 $) — 房间的尺寸。
第二行包含四个整数 $ a $, $ b $, $ f $, $ g $ ($ 0 < a, f < w $; $ 0 < b, g < d $): 笔记本电脑位于地面的点 $ (a, b) $,而投影仪悬挂在天花板上方的点 $ (f, g) $。
**输出格式**
对于每个测试案例,打印一个整数 — 连接笔记本电脑和投影仪的最短电缆长度,电缆只能沿着长方体的墙壁、地板和天花板平行于长方体的边缘。
**输入输出样例**
**输入样例 #1**
```
5
55 20 29
23 10 18 3
20 10 5
1 5 2 5
15 15 4
7 13 10 10
2 1000 2
1 1 1 999
10 4 10
7 1 2 1
```
**输出样例 #1**
```
47
8
14
1002
17
```
**说明**
题目描述中的图片展示了第一个测试案例。**平行投影** **题意翻译** - **本题一个测试点内有多组测试数据**。 - 在一个三维坐标系中有一个左下角坐标为 $(0,0,0)$,右上角坐标为 $(w,d,h)$ 的每条边都平行于坐标轴的长方体。 - 求从点 $(a,b,0)$ 到点 $(f,g,h)$ 满足以下条件的路线长度最小值: - 行走的每一段路都平行于坐标轴; - 路线应完全在长方体表面,不能离开长方体或进入长方体内部。 - $w,d,h\leq1000$,$0
**题意翻译**
- **本题一个测试点内有多组测试数据**。
- 在一个三维坐标系中有一个左下角坐标为 $(0,0,0)$,右上角坐标为 $(w,d,h)$ 的每条边都平行于坐标轴的长方体。
- 求从点 $(a,b,0)$ 到点 $(f,g,h)$ 满足以下条件的路线长度最小值:
- 行走的每一段路都平行于坐标轴;
- 路线应完全在长方体表面,不能离开长方体或进入长方体内部。
- $w,d,h\leq1000$,$0
**题目描述**
Vika's house has a room in the shape of a rectangular parallelepiped (also known as a rectangular cuboid). Its floor is a rectangle of size $ w \times d $, and the ceiling is right above at the constant height of $ h $. Let's introduce a coordinate system on the floor so that its corners are at points $ (0, 0) $, $ (w, 0) $, $ (w, d) $, and $ (0, d) $.
A laptop is standing on the floor at point $ (a, b) $. A projector is hanging on the ceiling right above point $ (f, g) $. Vika wants to connect the laptop and the projector with a cable in such a way that the cable always goes along the walls, ceiling, or floor (i.e., does not go inside the cuboid). Additionally, the cable should always run parallel to one of the cuboid's edges (i.e., it can not go diagonally).
What is the minimum length of a cable that can connect the laptop to the projector?
Illustration for the first test case. One of the optimal ways to put the cable is shown in green.
**输入输出格式**
**输入格式**
每个测试包含多个测试案例。第一行包含测试案例的数量 $ t $ ($ 1 \le t \le 10^4 $)。测试案例的描述如下。
每个测试案例的第一行包含三个整数 $ w $, $ d $, 和 $ h $ ($ 2 \le w, d, h \le 1000 $) — 房间的尺寸。
第二行包含四个整数 $ a $, $ b $, $ f $, $ g $ ($ 0 < a, f < w $; $ 0 < b, g < d $): 笔记本电脑位于地面的点 $ (a, b) $,而投影仪悬挂在天花板上方的点 $ (f, g) $。
**输出格式**
对于每个测试案例,打印一个整数 — 连接笔记本电脑和投影仪的最短电缆长度,电缆只能沿着长方体的墙壁、地板和天花板平行于长方体的边缘。
**输入输出样例**
**输入样例 #1**
```
5
55 20 29
23 10 18 3
20 10 5
1 5 2 5
15 15 4
7 13 10 10
2 1000 2
1 1 1 999
10 4 10
7 1 2 1
```
**输出样例 #1**
```
47
8
14
1002
17
```
**说明**
题目描述中的图片展示了第一个测试案例。**平行投影** **题意翻译** - **本题一个测试点内有多组测试数据**。 - 在一个三维坐标系中有一个左下角坐标为 $(0,0,0)$,右上角坐标为 $(w,d,h)$ 的每条边都平行于坐标轴的长方体。 - 求从点 $(a,b,0)$ 到点 $(f,g,h)$ 满足以下条件的路线长度最小值: - 行走的每一段路都平行于坐标轴; - 路线应完全在长方体表面,不能离开长方体或进入长方体内部。 - $w,d,h\leq1000$,$0