310184: CF1794E. Labeling the Tree with Distances
Memory Limit:256 MB
Time Limit:4 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Labeling the Tree with Distances
题目描述
You are given an unweighted tree of $ n $ vertices numbered from $ 1 $ to $ n $ and a list of $ n-1 $ integers $ a_1, a_2, \ldots, a_{n-1} $ . A tree is a connected undirected graph without cycles. You will use each element of the list to label one vertex. No vertex should be labeled twice. You can label the only remaining unlabeled vertex with any integer. A vertex $ x $ is called good if it is possible to do this labeling so that for each vertex $ i $ , its label is the distance between $ x $ and $ i $ . The distance between two vertices $ s $ and $ t $ on a tree is the minimum number of edges on a path that starts at vertex $ s $ and ends at vertex $ t $ . Find all good vertices.输入输出格式
输入格式
The first line contains one integer $ n $ ( $ 2\le n\le 2\cdot 10^5 $ ) — the number of vertices in the tree. The second line contains $ n - 1 $ integers $ a_1,a_2,\ldots,a_{n-1} $ ( $ 0\le a_i < n $ ) — the given list. Then, $ n−1 $ lines follow. Each of them contains two integers $ u $ and $ v $ ( $ 1\le u,v\le n $ ) denoting an edge between vertices $ u $ and $ v $ . It is guaranteed that the edges form a tree.
输出格式
In the first line print the number of good vertices. In the second line, print the indices of all good vertices in ascending order.
输入输出样例
输入样例 #1
6
2 1 0 1 2
1 2
2 3
2 4
4 5
4 6输出样例 #1
2
2 4输入样例 #2
5
1 2 1 2
1 2
3 2
3 4
5 4输出样例 #2
1
3输入样例 #3
3
2 2
1 2
2 3输出样例 #3
0说明
This is the tree for the first example: 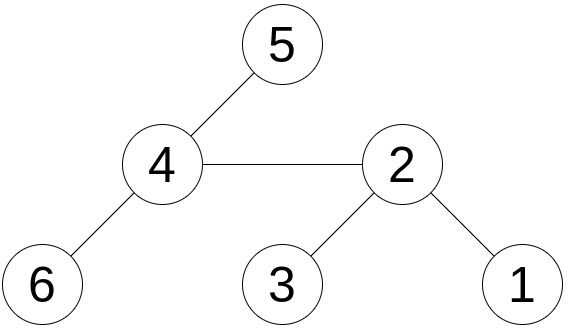And these are two possible labelings with the elements on the list so that $ 2 $ is a good vertex (left) and $ 4 $ is a good vertex (right). 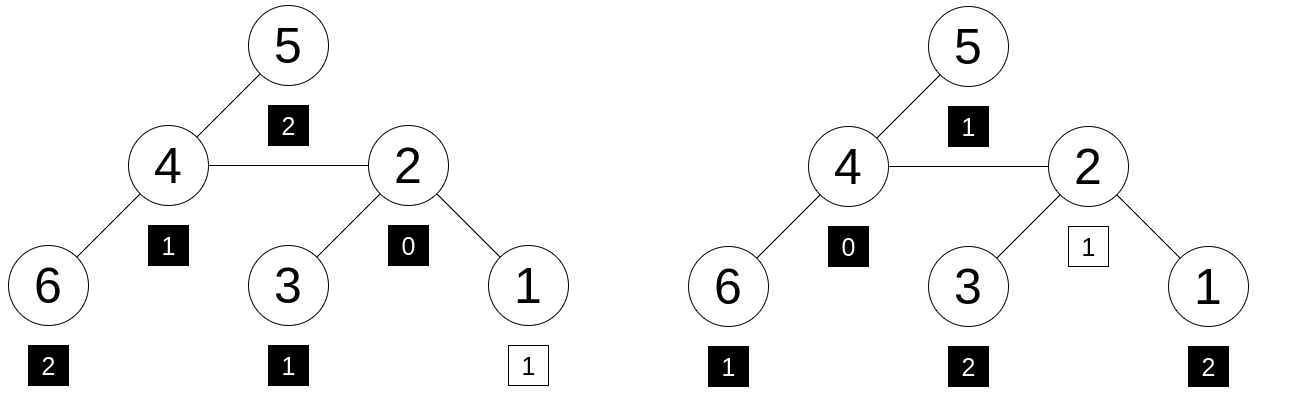The square below each vertex represents its label. The black squares contain the numbers which were on the given list and the only white square contains the only number which was not on the given list. In the second example, the only good vertex is vertex $ 3 $ . In the third example, there are no good vertices.Input
题意翻译
给你一个树,边权为 $1$。给定 $n-1$ 个数,你需要将这些数分配到 $n-1$ 个节点上。 一个点 $x$ 是好的,当且仅当存在一种分配方案,所有被分配数的点到 $x$ 的最短路径长度等于其被分配的数。 求所有好点。Output
**题目描述**
给定一个无权树,包含 $ n $ 个顶点,顶点编号从 $ 1 $ 到 $ n $,以及一个包含 $ n-1 $ 个整数的列表 $ a_1, a_2, \ldots, a_{n-1} $。树是一个没有环的连通无向图。您将使用列表中的每个元素来标记一个顶点。没有顶点应该被标记两次。您可以用任何整数标记剩下的唯一未标记顶点。
如果一个顶点 $ x $ 能够通过这种方式标记,使得对于每个顶点 $ i $,其标签是 $ x $ 和 $ i $ 之间的距离,则称该顶点 $ x $ 为“好的”。树上两个顶点 $ s $ 和 $ t $ 之间的距离是始于顶点 $ s $ 结束于顶点 $ t $ 的路径上的边的最小数目。
找出所有好的顶点。
**输入输出格式**
**输入格式**
第一行包含一个整数 $ n $($ 2 \le n \le 2 \times 10^5 $)——树中的顶点数。
第二行包含 $ n - 1 $ 个整数 $ a_1, a_2, \ldots, a_{n-1} $($ 0 \le a_i < n $)——给定的列表。
接下来 $ n-1 $ 行,每行包含两个整数 $ u $ 和 $ v $($ 1 \le u, v \le n $),表示顶点 $ u $ 和 $ v $ 之间的边。保证这些边构成一棵树。
**输出格式**
第一行输出好的顶点的数量。
第二行,按升序输出所有好的顶点的索引。
**输入输出样例**
**输入样例 #1**
```
6
2 1 0 1 2
1 2
2 3
2 4
4 5
4 6
```
**输出样例 #1**
```
2
2 4
```
**输入样例 #2**
```
5
1 2 1 2
1 2
3 2
3 4
5 4
```
**输出样例 #2**
```
1
3
```
**输入样例 #3**
```
3
2 2
1 2
2 3
```
**输出样例 #3**
```
0
```
**说明**
这是第一个示例的树:

这是两种可能的标记方式,使得 $ 2 $(左图)和 $ 4 $(右图)成为好的顶点。

每个顶点下方的正方形代表其标签。黑色正方形包含给定列表上的数字,唯一的白色正方形包含不在给定列表上的数字。
在第二个示例中,唯一好的顶点是顶点 $ 3 $。
在第三个示例中,没有好的顶点。**题目描述** 给定一个无权树,包含 $ n $ 个顶点,顶点编号从 $ 1 $ 到 $ n $,以及一个包含 $ n-1 $ 个整数的列表 $ a_1, a_2, \ldots, a_{n-1} $。树是一个没有环的连通无向图。您将使用列表中的每个元素来标记一个顶点。没有顶点应该被标记两次。您可以用任何整数标记剩下的唯一未标记顶点。 如果一个顶点 $ x $ 能够通过这种方式标记,使得对于每个顶点 $ i $,其标签是 $ x $ 和 $ i $ 之间的距离,则称该顶点 $ x $ 为“好的”。树上两个顶点 $ s $ 和 $ t $ 之间的距离是始于顶点 $ s $ 结束于顶点 $ t $ 的路径上的边的最小数目。 找出所有好的顶点。 **输入输出格式** **输入格式** 第一行包含一个整数 $ n $($ 2 \le n \le 2 \times 10^5 $)——树中的顶点数。 第二行包含 $ n - 1 $ 个整数 $ a_1, a_2, \ldots, a_{n-1} $($ 0 \le a_i < n $)——给定的列表。 接下来 $ n-1 $ 行,每行包含两个整数 $ u $ 和 $ v $($ 1 \le u, v \le n $),表示顶点 $ u $ 和 $ v $ 之间的边。保证这些边构成一棵树。 **输出格式** 第一行输出好的顶点的数量。 第二行,按升序输出所有好的顶点的索引。 **输入输出样例** **输入样例 #1** ``` 6 2 1 0 1 2 1 2 2 3 2 4 4 5 4 6 ``` **输出样例 #1** ``` 2 2 4 ``` **输入样例 #2** ``` 5 1 2 1 2 1 2 3 2 3 4 5 4 ``` **输出样例 #2** ``` 1 3 ``` **输入样例 #3** ``` 3 2 2 1 2 2 3 ``` **输出样例 #3** ``` 0 ``` **说明** 这是第一个示例的树:  这是两种可能的标记方式,使得 $ 2 $(左图)和 $ 4 $(右图)成为好的顶点。  每个顶点下方的正方形代表其标签。黑色正方形包含给定列表上的数字,唯一的白色正方形包含不在给定列表上的数字。 在第二个示例中,唯一好的顶点是顶点 $ 3 $。 在第三个示例中,没有好的顶点。
给定一个无权树,包含 $ n $ 个顶点,顶点编号从 $ 1 $ 到 $ n $,以及一个包含 $ n-1 $ 个整数的列表 $ a_1, a_2, \ldots, a_{n-1} $。树是一个没有环的连通无向图。您将使用列表中的每个元素来标记一个顶点。没有顶点应该被标记两次。您可以用任何整数标记剩下的唯一未标记顶点。
如果一个顶点 $ x $ 能够通过这种方式标记,使得对于每个顶点 $ i $,其标签是 $ x $ 和 $ i $ 之间的距离,则称该顶点 $ x $ 为“好的”。树上两个顶点 $ s $ 和 $ t $ 之间的距离是始于顶点 $ s $ 结束于顶点 $ t $ 的路径上的边的最小数目。
找出所有好的顶点。
**输入输出格式**
**输入格式**
第一行包含一个整数 $ n $($ 2 \le n \le 2 \times 10^5 $)——树中的顶点数。
第二行包含 $ n - 1 $ 个整数 $ a_1, a_2, \ldots, a_{n-1} $($ 0 \le a_i < n $)——给定的列表。
接下来 $ n-1 $ 行,每行包含两个整数 $ u $ 和 $ v $($ 1 \le u, v \le n $),表示顶点 $ u $ 和 $ v $ 之间的边。保证这些边构成一棵树。
**输出格式**
第一行输出好的顶点的数量。
第二行,按升序输出所有好的顶点的索引。
**输入输出样例**
**输入样例 #1**
```
6
2 1 0 1 2
1 2
2 3
2 4
4 5
4 6
```
**输出样例 #1**
```
2
2 4
```
**输入样例 #2**
```
5
1 2 1 2
1 2
3 2
3 4
5 4
```
**输出样例 #2**
```
1
3
```
**输入样例 #3**
```
3
2 2
1 2
2 3
```
**输出样例 #3**
```
0
```
**说明**
这是第一个示例的树:

这是两种可能的标记方式,使得 $ 2 $(左图)和 $ 4 $(右图)成为好的顶点。

每个顶点下方的正方形代表其标签。黑色正方形包含给定列表上的数字,唯一的白色正方形包含不在给定列表上的数字。
在第二个示例中,唯一好的顶点是顶点 $ 3 $。
在第三个示例中,没有好的顶点。**题目描述** 给定一个无权树,包含 $ n $ 个顶点,顶点编号从 $ 1 $ 到 $ n $,以及一个包含 $ n-1 $ 个整数的列表 $ a_1, a_2, \ldots, a_{n-1} $。树是一个没有环的连通无向图。您将使用列表中的每个元素来标记一个顶点。没有顶点应该被标记两次。您可以用任何整数标记剩下的唯一未标记顶点。 如果一个顶点 $ x $ 能够通过这种方式标记,使得对于每个顶点 $ i $,其标签是 $ x $ 和 $ i $ 之间的距离,则称该顶点 $ x $ 为“好的”。树上两个顶点 $ s $ 和 $ t $ 之间的距离是始于顶点 $ s $ 结束于顶点 $ t $ 的路径上的边的最小数目。 找出所有好的顶点。 **输入输出格式** **输入格式** 第一行包含一个整数 $ n $($ 2 \le n \le 2 \times 10^5 $)——树中的顶点数。 第二行包含 $ n - 1 $ 个整数 $ a_1, a_2, \ldots, a_{n-1} $($ 0 \le a_i < n $)——给定的列表。 接下来 $ n-1 $ 行,每行包含两个整数 $ u $ 和 $ v $($ 1 \le u, v \le n $),表示顶点 $ u $ 和 $ v $ 之间的边。保证这些边构成一棵树。 **输出格式** 第一行输出好的顶点的数量。 第二行,按升序输出所有好的顶点的索引。 **输入输出样例** **输入样例 #1** ``` 6 2 1 0 1 2 1 2 2 3 2 4 4 5 4 6 ``` **输出样例 #1** ``` 2 2 4 ``` **输入样例 #2** ``` 5 1 2 1 2 1 2 3 2 3 4 5 4 ``` **输出样例 #2** ``` 1 3 ``` **输入样例 #3** ``` 3 2 2 1 2 2 3 ``` **输出样例 #3** ``` 0 ``` **说明** 这是第一个示例的树:  这是两种可能的标记方式,使得 $ 2 $(左图)和 $ 4 $(右图)成为好的顶点。  每个顶点下方的正方形代表其标签。黑色正方形包含给定列表上的数字,唯一的白色正方形包含不在给定列表上的数字。 在第二个示例中,唯一好的顶点是顶点 $ 3 $。 在第三个示例中,没有好的顶点。