Candy Store

题意翻译

有 $n$ 种糖，第 $i$ 种糖有 $a_i$ 块，每块 $b_i$ 元。对每种糖，你要选择一个 $d_i | a_i$，然后每 $d_i$ 块糖装进一个袋子。 现在把糖摆上货架，第 $i$ 类糖的价签上的价格 $c_i$ 是一袋子 $i$ 类糖的价值，即 $c_i = d_i \times b_i$。 对于货架上一个区间 $[l, r]$，如果他们的价签相同，即 $c_l = c_{l + 1} = \dots = c_r$，则他们可以共用一个价签。 请问最少需要多少价签？ 多组数据，保证 $n$ 之和不超过 $2 \times 10^5$，$1 \leq a_i \leq 10^9$，$1 \leq b_i \leq 10^4$。 provider：一扶苏一

题目描述

The store sells $ n $ types of candies with numbers from $ 1 $ to $ n $ . One candy of type $ i $ costs $ b_i $ coins. In total, there are $ a_i $ candies of type $ i $ in the store. You need to pack all available candies in packs, each pack should contain only one type of candies. Formally, for each type of candy $ i $ you need to choose the integer $ d_i $ , denoting the number of type $ i $ candies in one pack, so that $ a_i $ is divided without remainder by $ d_i $ . Then the cost of one pack of candies of type $ i $ will be equal to $ b_i \cdot d_i $ . Let's denote this cost by $ c_i $ , that is, $ c_i = b_i \cdot d_i $ . After packaging, packs will be placed on the shelf. Consider the cost of the packs placed on the shelf, in order $ c_1, c_2, \ldots, c_n $ . Price tags will be used to describe costs of the packs. One price tag can describe the cost of all packs from $ l $ to $ r $ inclusive if $ c_l = c_{l+1} = \ldots = c_r $ . Each of the packs from $ 1 $ to $ n $ must be described by at least one price tag. For example, if $ c_1, \ldots, c_n = [4, 4, 2, 4, 4] $ , to describe all the packs, a $ 3 $ price tags will be enough, the first price tag describes the packs $ 1, 2 $ , the second: $ 3 $ , the third: $ 4, 5 $ . You are given the integers $ a_1, b_1, a_2, b_2, \ldots, a_n, b_n $ . Your task is to choose integers $ d_i $ so that $ a_i $ is divisible by $ d_i $ for all $ i $ , and the required number of price tags to describe the values of $ c_1, c_2, \ldots, c_n $ is the minimum possible. For a better understanding of the statement, look at the illustration of the first test case of the first test: 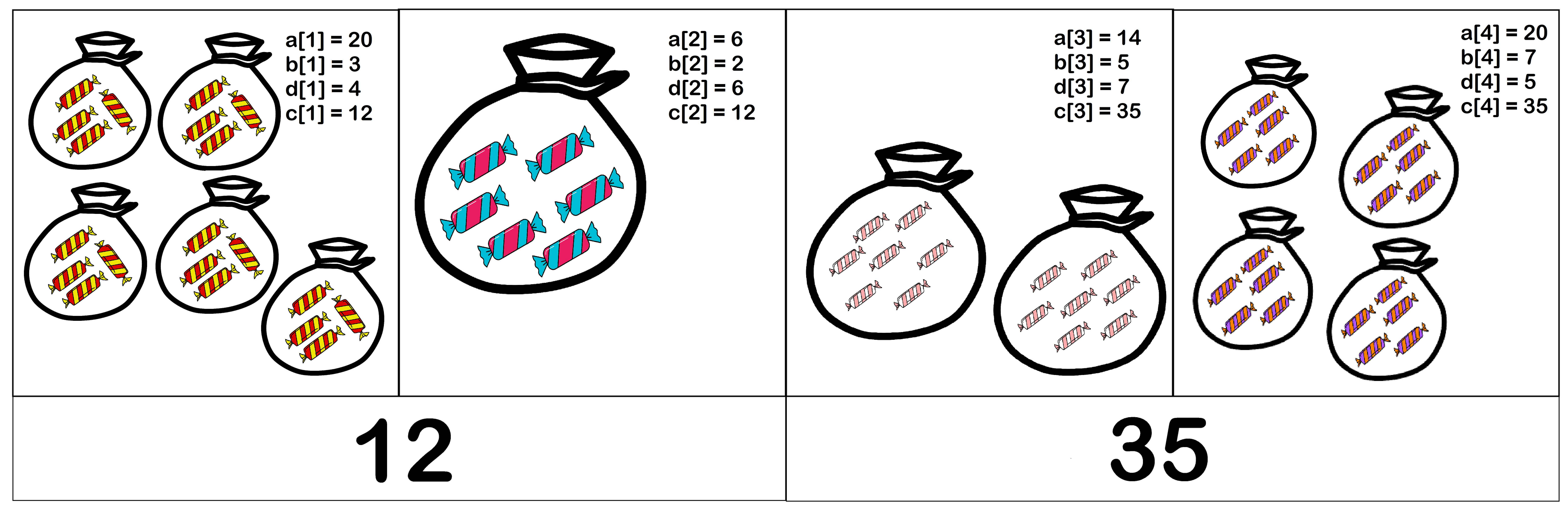Let's repeat the meaning of the notation used in the problem: $ a_i $ — the number of candies of type $ i $ available in the store. $ b_i $ — the cost of one candy of type $ i $ . $ d_i $ — the number of candies of type $ i $ in one pack. $ c_i $ — the cost of one pack of candies of type $ i $ is expressed by the formula $ c_i = b_i \cdot d_i $ .

输入输出格式

输入格式

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 100\,000 $ ). Description of the test cases follows. The first line of each test case contains a single integer $ n $ ( $ 2 \le n \le 200\,000 $ ) — the number of types of candies. Each of the next $ n $ lines of each test case contains two integers $ a_i $ and $ b_i $ ( $ 1 \le a_i \le 10^9 $ , $ 1 \le b_i \le 10\,000 $ ) — the number of candies and the cost of one candy of type $ i $ , respectively. It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 200\,000 $ .

输出格式

For each test case, output the minimum number of price tags required to describe the costs of all packs of candies in the store.

输入输出样例

输入样例 #1

5
4
20 3
6 2
14 5
20 7
3
444 5
2002 10
2020 2
5
7 7
6 5
15 2
10 3
7 7
5
10 1
11 5
5 1
2 2
8 2
6
7 12
12 3
5 3
9 12
9 3
1000000000 10000

输出样例 #1

2
1
3
2
5

说明

In the first test case, you can choose $ d_1 = 4 $ , $ d_2 = 6 $ , $ d_3 = 7 $ , $ d_4 = 5 $ . Then the cost of packs will be equal to $ [12, 12, 35, 35] $ . $ 2 $ price tags are enough to describe them, the first price tag for $ c_1, c_2 $ and the second price tag for $ c_3, c_4 $ . It can be shown that with any correct choice of $ d_i $ , at least $ 2 $ of the price tag will be needed to describe all the packs. Also note that this example is illustrated by a picture in the statement. In the second test case, with $ d_1 = 4 $ , $ d_2 = 2 $ , $ d_3 = 10 $ , the costs of all packs will be equal to $ 20 $ . Thus, $ 1 $ price tag is enough to describe all the packs. Note that $ a_i $ is divisible by $ d_i $ for all $ i $ , which is necessary condition. In the third test case, it is not difficult to understand that one price tag can be used to describe $ 2 $ nd, $ 3 $ rd and $ 4 $ th packs. And additionally a price tag for pack $ 1 $ and pack $ 5 $ . Total: $ 3 $ price tags.

题目大意：
糖果店里有n种糖果，第i种糖果有a_i块，每块b_i元。对于每种糖果，需要选择一个d_i，使得a_i能被d_i整除，然后将每d_i块糖装进一个袋子。每种糖果的价签c_i是一袋子的价值，即c_i = d_i * b_i。如果货架上一段区间[l, r]的价签相同，即c_l = c_{l+1} = ... = c_r，那么它们可以共用一个价签。问最少需要多少价签？

输入输出数据格式：
输入：
- 第一行包含一个整数t(1≤t≤100,000)，表示测试用例的数量。
- 每个测试用例的第一行包含一个整数n(2≤n≤200,000)，表示糖果的种类数。
- 接下来的n行，每行包含两个整数a_i和b_i(1≤a_i≤10^9,1≤b_i≤10,000)，分别表示第i种糖果的数量和单价。

输出：
- 对于每个测试用例，输出一个整数，表示描述所有糖果包装的最少价签数量。

示例输入输出：
输入：
```
5
4
20 3
6 2
14 5
20 7
3
444 5
2002 10
2020 2
5
7 7
6 5
15 2
10 3
7 7
5
10 1
11 5
5 1
2 2
8 2
6
7 12
12 3
5 3
9 12
9 3
1000000000 10000
```
输出：
```
2
1
3
2
5
```题目大意： 糖果店里有n种糖果，第i种糖果有a_i块，每块b_i元。对于每种糖果，需要选择一个d_i，使得a_i能被d_i整除，然后将每d_i块糖装进一个袋子。每种糖果的价签c_i是一袋子的价值，即c_i = d_i * b_i。如果货架上一段区间[l, r]的价签相同，即c_l = c_{l+1} = ... = c_r，那么它们可以共用一个价签。问最少需要多少价签？ 输入输出数据格式： 输入： - 第一行包含一个整数t(1≤t≤100,000)，表示测试用例的数量。 - 每个测试用例的第一行包含一个整数n(2≤n≤200,000)，表示糖果的种类数。 - 接下来的n行，每行包含两个整数a_i和b_i(1≤a_i≤10^9,1≤b_i≤10,000)，分别表示第i种糖果的数量和单价。 输出： - 对于每个测试用例，输出一个整数，表示描述所有糖果包装的最少价签数量。 示例输入输出： 输入： ``` 5 4 20 3 6 2 14 5 20 7 3 444 5 2002 10 2020 2 5 7 7 6 5 15 2 10 3 7 7 5 10 1 11 5 5 1 2 2 8 2 6 7 12 12 3 5 3 9 12 9 3 1000000000 10000 ``` 输出： ``` 2 1 3 2 5 ```