310254: CF1805E. There Should Be a Lot of Maximums

E. There Should Be a Lot of Maximumstime limit per test1 secondmemory limit per test256 megabytesinputstandard inputoutputstandard output

You are given a tree (a connected graph without cycles). Each vertex of the tree contains an integer. Let's define the $\mathrm{MAD}$ (maximum double) parameter of the tree as the maximum integer that occurs in the vertices of the tree at least $2$ times. If no number occurs in the tree more than once, then we assume $\mathrm{MAD}=0$.

Note that if you remove an edge from the tree, it splits into two trees. Let's compute the $\mathrm{MAD}$ parameters of the two trees and take the maximum of the two values. Let the result be the value of the deleted edge.

For each edge, find its value. Note that we don't actually delete any edges from the tree, the values are to be found independently.

Input

The first line contains one integer $n$ ($2 \le n \le 10^5$) — the number of vertices in the tree.

Each of the next $n - 1$ lines contains two integers $u$ and $v$ ($1 \le u, v \le n$) — the ends of an edge of the tree. It's guaranteed that the given edges form a valid tree.

The last line contains $n$ integers $a_1, a_2, \ldots, a_n$ ($1 \le a_i \le 10^9$) — the numbers in the vertices.

Output

For each edge in the input order, print one number — the maximum of the $\mathrm{MAD}$ parameters of the two trees obtained after removing the given edge from the initial tree.

ExamplesInput

5
1 2
2 3
2 4
1 5
2 1 3 2 1

Output

0
2
1
2

Input

6
1 2
1 3
1 4
4 5
4 6
1 2 3 1 4 5

Output

1
1
0
1
1

Note

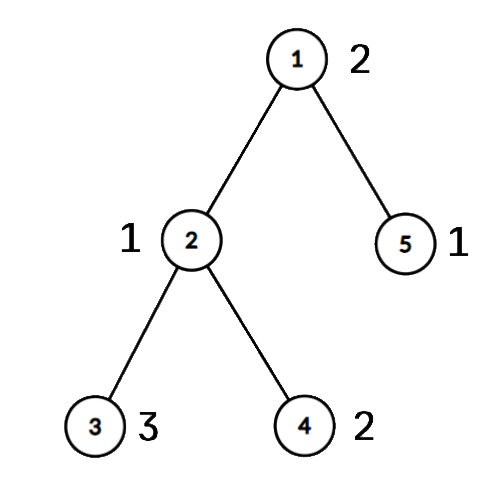
In the first example, after removing edge $(1, 2)$ no number repeats $2$ times in any of the resulting subtrees, so the answer is $\max(0, 0)=0$.

After removing edge $(2, 3)$, in the bigger subtree, $1$ is repeated twice, and $2$ is repeated twice, so the $\mathrm{MAD}$ of this tree is $2$.

After removing edge $(2, 4)$, in the bigger subtree, only the number $1$ is repeated, and in the second subtree, only one number appears, so the answer is $1$.

In the second example, if edge $1 \leftrightarrow 4$ is not removed, then one of the subtrees will have two $1$, so the answer — $1$. And if edge $1 \leftrightarrow 4$ is deleted, both subtrees have no repeating values, so the answer is $0$.

题目大意：
给定一棵树（无环的连通图），每个顶点含有一个整数。定义树的一个参数\(\text{MAD}\)（最大双倍）为在树的顶点中出现至少两次的最大整数。如果树中没有数字出现超过一次，则认为\(\text{MAD}=0\)。

当从树中移除一条边时，树会分成两棵树。计算这两棵树的\(\text{MAD}\)参数，并取两个值中的最大者作为删除边的“值”。

对于每条边，找出其“值”。注意，实际上并没有从树中删除任何边，这些值是独立计算的。

输入输出数据格式：
输入：
- 第一行包含一个整数\(n\) (\(2 \le n \le 10^5\)) —— 树的顶点数。
- 接下来的\(n - 1\)行，每行包含两个整数\(u\)和\(v\) (\(1 \le u, v \le n\)) —— 树的一条边的两个端点。保证给定的边形成一棵有效的树。
- 最后一行包含\(n\)个整数\(a_1, a_2, \ldots, a_n\) (\(1 \le a_i \le 10^9\)) —— 顶点中的数字。

输出：
- 对于输入顺序中的每条边，输出一个数字 —— 在从初始树中删除给定边后得到的两棵树的\(\text{MAD}\)参数的最大值。题目大意： 给定一棵树（无环的连通图），每个顶点含有一个整数。定义树的一个参数\(\text{MAD}\)（最大双倍）为在树的顶点中出现至少两次的最大整数。如果树中没有数字出现超过一次，则认为\(\text{MAD}=0\)。 当从树中移除一条边时，树会分成两棵树。计算这两棵树的\(\text{MAD}\)参数，并取两个值中的最大者作为删除边的“值”。 对于每条边，找出其“值”。注意，实际上并没有从树中删除任何边，这些值是独立计算的。 输入输出数据格式： 输入： - 第一行包含一个整数\(n\) (\(2 \le n \le 10^5\)) —— 树的顶点数。 - 接下来的\(n - 1\)行，每行包含两个整数\(u\)和\(v\) (\(1 \le u, v \le n\)) —— 树的一条边的两个端点。保证给定的边形成一棵有效的树。 - 最后一行包含\(n\)个整数\(a_1, a_2, \ldots, a_n\) (\(1 \le a_i \le 10^9\)) —— 顶点中的数字。 输出： - 对于输入顺序中的每条边，输出一个数字 —— 在从初始树中删除给定边后得到的两棵树的\(\text{MAD}\)参数的最大值。