310340: CF1820D. The Butcher

D. The Butchertime limit per test2 secondsmemory limit per test256 megabytesinputstandard inputoutputstandard output

Anton plays his favorite game "Defense of The Ancients 2" for his favorite hero — The Butcher. Now he wants to make his own dinner. To do this he will take a rectangle of height $h$ and width $w$, then make a vertical or horizontal cut so that both resulting parts have integer sides. After that, he will put one of the parts in the box and cut the other again, and so on.

More formally, a rectangle of size $h \times w$ can be cut into two parts of sizes $x \times w$ and $(h - x) \times w$, where $x$ is an integer from $1$ to $(h - 1)$, or into two parts of sizes $h \times y$ and $h \times (w - y)$, where $y$ is an integer from $1$ to $(w - 1)$.

He will repeat this operation $n - 1$ times, and then put the remaining rectangle into the box too. Thus, the box will contain $n$ rectangles, of which $n - 1$ rectangles were put in the box as a result of the cuts, and the $n$-th rectangle is the one that the Butcher has left after all $n - 1$ cuts.

Unfortunately, Butcher forgot the numbers $h$ and $w$, but he still has $n$ rectangles mixed in random order. Note that Butcher didn't rotate the rectangles, but only shuffled them. Now he wants to know all possible pairs $(h, w)$ from which this set of rectangles can be obtained. And you have to help him do it!

It is guaranteed that there exists at least one pair $(h, w)$ from which this set of rectangles can be obtained.

Input

Each test consists of multiple test cases. The first line contains a single integer $t$ ($1 \le t \le 10^4$) — the number of test cases. The description of test cases follows.

The first line of each test case contains a single integer $n$ ($1 \le n \le 2 \cdot 10^5$) — the number of rectangles obtained.

The $i$-th of the next $n$ lines contains two integers $a_i$ and $b_i$ ($1 \le a_i, b_i \le 10^6$) — the height and width of the $i$-th rectangle.

It is guaranteed that the sum of $n$ over all test cases does not exceed $2 \cdot 10^5$.

Output

For each test case, on the first line output a single integer $m$ — the number of pairs $(h, w)$ denoting the sizes of rectangles from which the given rectangles can be obtained. Two rectangles are considered different if they have different heights or widths.

On each of the following $m$ lines print output integers $h_i$ and $w_i$ — the height and width of the rectangle from which the given rectangles can be obtained. You can output the rectangles in any order.

ExampleInput

4
3
1 2
3 5
1 3
3
1 1
1 1
1 1
1
10 10
4
3 2
5 5
2 2
8 7

Output

1
4 5
2
1 3
3 1
1
10 10
1
13 7

Note

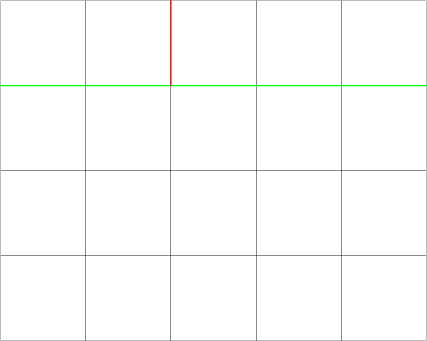
In the first test case, Butcher could only have a rectangle of size $4 \times 5$. Then the cuts could look like this (first the green cut was made, then the red one):

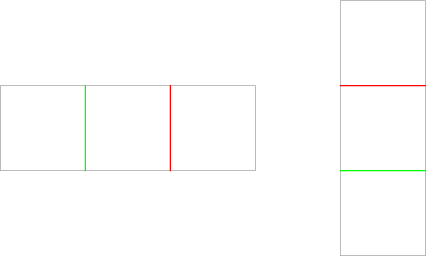
In the second test case, Butcher could have either a rectangle of $1 \times 3$ or $3 \times 1$. The cuts would have looked like this (first the green cut was made, then the red cut):

In the third test case, Butcher did not make any cuts, so the rectangle is $10 \times 10$.

题目大意：
一个游戏玩家在玩他的游戏时，想要制作自己的晚餐。他会取一个高为 $ h $，宽为 $ w $ 的矩形，然后进行一次垂直或水平切割，使得两个结果部分都有整数的边长。之后，他会将其中一部分放入盒子中，然后继续切割另一部分，如此重复。具体来说，一个大小为 $ h \times w $ 的矩形可以被切割成两个大小分别为 $ x \times w $ 和 $ (h - x) \times w $ 的部分，其中 $ x $ 是从 1 到 $ h - 1 $ 的整数，或者可以被切割成两个大小分别为 $ h \times y $ 和 $ h \times (w - y) $ 的部分，其中 $ y $ 是从 1 到 $ w - 1 $ 的整数。他会重复这个操作 $ n - 1 $ 次，然后将剩余的矩形也放入盒子中。这样，盒子里将包含 $ n $ 个矩形，其中 $ n - 1 $ 个矩形是通过切割放入盒子的，第 $ n $ 个矩形是经过所有 $ n - 1 $ 次切割后剩下的矩形。

输入输出数据格式：
输入：
- 第一行包含一个整数 $ t $（$ 1 \le t \le 10^4 $），表示测试用例的数量。
- 每个测试用例的第一行包含一个整数 $ n $（$ 1 \le n \le 2 \cdot 10^5 $），表示获得的矩形的数量。
- 接下来的 $ n $ 行，每行包含两个整数 $ a_i $ 和 $ b_i $（$ 1 \le a_i, b_i \le 10^6 $），表示第 $ i $ 个矩形的高度和宽度。

输出：
- 对于每个测试用例，第一行输出一个整数 $ m $，表示可以从中获得给定矩形的矩形大小 $ (h, w) $ 的对数。
- 接下来的 $ m $ 行，每行输出两个整数 $ h_i $ 和 $ w_i $，表示可以获得给定矩形的矩形的高度和宽度。可以按任意顺序输出矩形。

请注意，题目保证至少存在一个 $ (h, w) $ 的对，可以从该对中获得给定的矩形集。题目大意： 一个游戏玩家在玩他的游戏时，想要制作自己的晚餐。他会取一个高为 $ h $，宽为 $ w $ 的矩形，然后进行一次垂直或水平切割，使得两个结果部分都有整数的边长。之后，他会将其中一部分放入盒子中，然后继续切割另一部分，如此重复。具体来说，一个大小为 $ h \times w $ 的矩形可以被切割成两个大小分别为 $ x \times w $ 和 $ (h - x) \times w $ 的部分，其中 $ x $ 是从 1 到 $ h - 1 $ 的整数，或者可以被切割成两个大小分别为 $ h \times y $ 和 $ h \times (w - y) $ 的部分，其中 $ y $ 是从 1 到 $ w - 1 $ 的整数。他会重复这个操作 $ n - 1 $ 次，然后将剩余的矩形也放入盒子中。这样，盒子里将包含 $ n $ 个矩形，其中 $ n - 1 $ 个矩形是通过切割放入盒子的，第 $ n $ 个矩形是经过所有 $ n - 1 $ 次切割后剩下的矩形。 输入输出数据格式： 输入： - 第一行包含一个整数 $ t $（$ 1 \le t \le 10^4 $），表示测试用例的数量。 - 每个测试用例的第一行包含一个整数 $ n $（$ 1 \le n \le 2 \cdot 10^5 $），表示获得的矩形的数量。 - 接下来的 $ n $ 行，每行包含两个整数 $ a_i $ 和 $ b_i $（$ 1 \le a_i, b_i \le 10^6 $），表示第 $ i $ 个矩形的高度和宽度。 输出： - 对于每个测试用例，第一行输出一个整数 $ m $，表示可以从中获得给定矩形的矩形大小 $ (h, w) $ 的对数。 - 接下来的 $ m $ 行，每行输出两个整数 $ h_i $ 和 $ w_i $，表示可以获得给定矩形的矩形的高度和宽度。可以按任意顺序输出矩形。 请注意，题目保证至少存在一个 $ (h, w) $ 的对，可以从该对中获得给定的矩形集。