310374: CF1823F. Random Walk

F. Random Walktime limit per test2 secondsmemory limit per test256 megabytesinputstandard inputoutputstandard output

You are given a tree consisting of $n$ vertices and $n - 1$ edges, and each vertex $v$ has a counter $c(v)$ assigned to it.

Initially, there is a chip placed at vertex $s$ and all counters, except $c(s)$, are set to $0$; $c(s)$ is set to $1$.

Your goal is to place the chip at vertex $t$. You can achieve it by a series of moves. Suppose right now the chip is placed at the vertex $v$. In one move, you do the following:

1. choose one of neighbors $to$ of vertex $v$ uniformly at random ($to$ is neighbor of $v$ if and only if there is an edge $\{v, to\}$ in the tree);
2. move the chip to vertex $to$ and increase $c(to)$ by $1$;

You'll repeat the move above until you reach the vertex $t$.

For each vertex $v$ calculate the expected value of $c(v)$ modulo $998\,244\,353$.

Input

The first line contains three integers $n$, $s$ and $t$ ($2 \le n \le 2 \cdot 10^5$; $1 \le s, t \le n$; $s \neq t$) — number of vertices in the tree and the starting and finishing vertices.

Next $n - 1$ lines contain edges of the tree: one edge per line. The $i$-th line contains two integers $u_i$ and $v_i$ ($1 \le u_i, v_i \le n$; $u_i \neq v_i$), denoting the edge between the nodes $u_i$ and $v_i$.

It's guaranteed that the given edges form a tree.

Output

Print $n$ numbers: expected values of $c(v)$ modulo $998\,244\,353$ for each $v$ from $1$ to $n$.

Formally, let $M = 998\,244\,353$. It can be shown that the answer can be expressed as an irreducible fraction $\frac{p}{q}$, where $p$ and $q$ are integers and $q \not \equiv 0 \pmod{M}$. Output the integer equal to $p \cdot q^{-1} \bmod M$. In other words, output such an integer $x$ that $0 \le x < M$ and $x \cdot q \equiv p \pmod{M}$.

ExamplesInput

3 1 3
1 2
2 3

Output

2 2 1 

Input

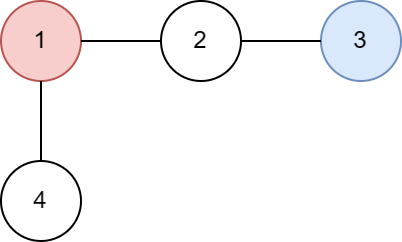
4 1 3
1 2
2 3
1 4

Output

4 2 1 2 

Input

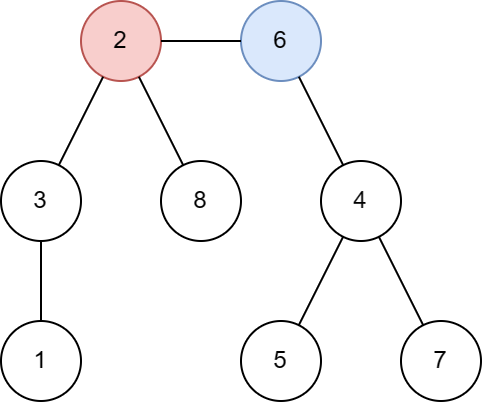
8 2 6
6 4
6 2
5 4
3 1
2 3
7 4
8 2

Output

1 3 2 0 0 1 0 1 

Note

The tree from the first example is shown below:

Let's calculate expected value $E[c(1)]$:

• $P(c(1) = 0) = 0$, since $c(1)$ is set to $1$ from the start.
• $P(c(1) = 1) = \frac{1}{2}$, since there is the only one series of moves that leads $c(1) = 1$. It's $1 \rightarrow 2 \rightarrow 3$ with probability $1 \cdot \frac{1}{2}$.
• $P(c(1) = 2) = \frac{1}{4}$: the only path is $1 \rightarrow_{1} 2 \rightarrow_{0.5} 1 \rightarrow_{1} 2 \rightarrow_{0.5} 3$.
• $P(c(1) = 3) = \frac{1}{8}$: the only path is $1 \rightarrow_{1} 2 \rightarrow_{0.5} 1 \rightarrow_{1} 2 \rightarrow_{0.5} 1 \rightarrow_{1} 2 \rightarrow_{0.5} 3$.
• $P(c(1) = i) = \frac{1}{2^i}$ in general case.

As a result, $E[c(1)] = \sum\limits_{i=1}^{\infty}{i \frac{1}{2^i}} = 2$. Image of tree in second test Image of tree in third test

题目大意：
给定一个包含n个顶点和n-1条边的树，每个顶点v都有一个计数器c(v)与之关联。初始时，一个筹码放在顶点s上，除了c(s)之外的所有计数器都设置为0；c(s)设置为1。目标是使筹码到达顶点t。可以通过一系列移动来实现。假设现在筹码放在顶点v上。在一次移动中，执行以下操作：

1. 随机均匀地选择顶点v的一个邻居to（to是v的邻居，当且仅当树中存在边{v, to}）；
2. 将筹码移动到顶点to并增加c(to)的值1；

重复上述移动，直到达到顶点t。

对于每个顶点v，计算c(v)的期望值模998,244,353。

输入输出数据格式：
输入：
第一行包含三个整数n、s和t（2≤n≤2×10^5；1≤s,t≤n；s≠t）——树中顶点的数量和起始及结束顶点。
接下来n-1行包含树的边：每行一个边。第i行包含两个整数u_i和v_i（1≤u_i,v_i≤n；u_i≠v_i），表示节点u_i和v_i之间的边。
保证给定的边构成一棵树。

输出：
打印n个数字：每个顶点v的c(v)的期望值模998,244,353，对于v从1到n。
形式上，设M=998,244,353。可以看出答案可以表示为不可约分数p/q，其中p和q是整数，且q≢0(mod M)。输出整数等于p⋅q^(-1)mod M。换句话说，输出一个整数x，使得0≤x