310385: CF1825D2. LuoTianyi and the Floating Islands (Hard Version)

D2. LuoTianyi and the Floating Islands (Hard Version)time limit per test2 secondsmemory limit per test256 megabytesinputstandard inputoutputstandard output

This is the hard version of the problem. The only difference is that in this version $k\le n$. You can make hacks only if both versions of the problem are solved.

Chtholly and the floating islands.

LuoTianyi now lives in a world with $n$ floating islands. The floating islands are connected by $n-1$ undirected air routes, and any two of them can reach each other by passing the routes. That means, the $n$ floating islands form a tree.

One day, LuoTianyi wants to meet her friends: Chtholly, Nephren, William, .... Totally, she wants to meet $k$ people. She doesn't know the exact positions of them, but she knows that they are in pairwise distinct islands. She define an island is good if and only if the sum of the distances$^{\dagger}$ from it to the islands with $k$ people is the minimal among all the $n$ islands.

Now, LuoTianyi wants to know that, if the $k$ people are randomly set in $k$ distinct of the $n$ islands, then what is the expect number of the good islands? You just need to tell her the expect number modulo $10^9+7$.

$^{\dagger}$The distance between two islands is the minimum number of air routes you need to take to get from one island to the other.

Input

The first line contains two integers $n$ and $k$ ($1\le k \le n \le 2\cdot 10^5$) — the number of the islands and people respectively.

Next $n−1$ lines describe the air routes. The $i$-th of them contains two integers $u_i$ and $v_i$ ($1 \le u_i,v_i \le n, u_i \neq v_i$) — the islands connected by the $i$-th air route.

Output

Print a single integer — the expect number of the good islands modulo $10^9 + 7$.

Formally, let $M = 10^9 + 7$. It can be shown that the answer can be expressed as an irreducible fraction $\frac{p}{q}$, where $p$ and $q$ are integers and $q \not \equiv 0$ ($\operatorname{mod} M$). Output the integer equal to $p \cdot q^{-1}$ $\operatorname{mod} M$. In other words, output such an integer $x$ that $0 \le x < M$ and $x \cdot q \equiv p$ ($\operatorname{mod} M$).

ExamplesInput

4 2
1 2
2 3
3 4

Output

666666674

Input

5 5
1 2
2 3
3 4
3 5

Output

1

Note

In the first example the air routes form the following tree:

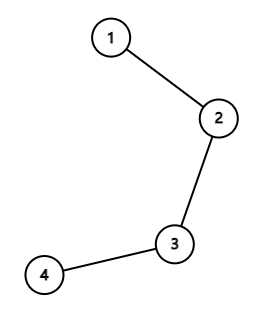
If the people are in the islands $1$ and $2$, then islands $1$ and $2$ will be good.

The sum of the distances from island $1$ or $2$ to all the people is $1+0=1$, which is the minimal. While the sum of the distances from island $3$ to all the people is $2+1=3$, which is greater than $1$.

Like this, when the people are in island $1$ and $3$, then islands $1,2$ and $3$ will be good.

When the people are in islands $1$ and $4$, then islands $1,2,3$ and $4$ will be good.

When the people are in islands $2$ and $3$, then islands $2$ and $3$ will be good.

When the people are in islands $2$ and $4$, then islands $2,3$ and $4$ will be good.

When the people are in islands $3$ and $4$, then islands $3$ and $4$ will be good.

So the expect of the number of the good islands is $\frac{16}{6}$, which equals to $666666674$ modulo $10^9+7$.

In the second example the air routes form the following tree:

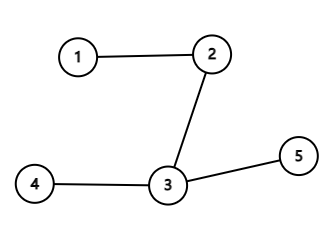
We can see that there is one person in each island, and only the island $3$ is good. So the expect number is $1$.

题目大意：

这是一个难题的困难版本。唯一的不同是，在这个版本中，k≤n。只有当问题的两个版本都被解决时，你才能进行hack操作。

洛天依现在生活在一个有n个漂浮岛屿的世界里。漂浮岛屿通过n-1条无向航线相连，任何两个岛屿都可以通过航线相互到达。这意味着，n个漂浮岛屿形成了一棵树。

有一天，洛天依想见她的朋友们：克托莉，涅墨西斯，威廉，……总共，她想见k个人。她不知道他们的确切位置，但她知道他们分别在不同的岛屿上。她定义一个岛屿是“好的”，当且仅当它到这k个岛屿的距离之和在所有n个岛屿中是最小的。

现在，洛天依想知道，如果k个人随机地被安排在n个岛屿中的k个不同的岛屿上，那么“好的岛屿”的期望数量是多少？你只需要告诉她这个期望数模10^9+7的结果。

输入输出数据格式：

输入：

第一行包含两个整数n和k（1≤k≤n≤2×10^5）——岛屿的数量和人数。

接下来n-1行描述航线。第i行包含两个整数u_i和v_i（1≤u_i,v_i≤n，u_i≠v_i）——第i条航线连接的岛屿。

输出：

打印一个整数——好的岛屿的期望数量模10^9+7。

形式上，设M=10^9+7。可以证明答案可以表示为一个不可约分数p/q，其中p和q是整数，且q≢0（mod M）。输出等于p⋅q^(-1)（mod M）的整数。换句话说，输出一个满足0≤x