310446: CF1834F. Typewriter
Description
Recently, Polycarp was given an unusual typewriter as a gift! Unfortunately, the typewriter was defective and had a rather strange design.
The typewriter consists of $n$ cells numbered from left to right from $1$ to $n$, and a carriage that moves over them. The typewriter cells contain $n$ distinct integers from $1$ to $n$, and each cell $i$ initially contains the integer $p_i$. Before all actions, the carriage is at cell number $1$ and there is nothing in its buffer storage. The cell on which the carriage is located is called the current cell.
The carriage can perform five types of operations:
- Take the integer from the current cell, if it is not empty, and put it in the carriage buffer, if it is empty (this buffer can contain no more than one integer).
- Put the integer from the carriage buffer, if it is not empty, into the current cell, if it is empty.
- Swap the number in the carriage buffer with the number in the current cell, if both the buffer and the cell contain integers.
- Move the carriage from the current cell $i$ to cell $i + 1$ (if $i < n$), while the integer in the buffer is preserved.
- Reset the carriage, i.e. move it to cell number $1$, while the integer in the buffer is preserved.
Polycarp was very interested in this typewriter, so he asks you to help him understand it and will ask you $q$ queries of three types:
- Perform a cyclic shift of the sequence $p$ to the left by $k_j$.
- Perform a cyclic shift of the sequence $p$ to the right by $k_j$.
- Reverse the sequence $p$.
Before and after each query, Polycarp wants to know what minimum number of carriage resets is needed for the current sequence in order to distribute the numbers to their cells (so that the number $i$ ends up in cell number $i$).
Note that Polycarp only wants to know the minimum number of carriage resets required to arrange the numbers in their places, but he does not actually distribute them.
Help Polycarp find the answers to his queries!
InputThe first line contains a single integer $n$ ($1 \le n \le 4 \cdot 10^5$) — the number of cells.
The second line contains $n$ distinct integers $p_1, p_2, \ldots, p_n$ ($1 \le p_i \le n$) — the initial arrangement of integers in the cells.
The third line contains a single integer $q$ ($0 \le q \le 4 \cdot 10^5$) — the number of queries.
Each of the next $q$ lines describes a query from Polycarp:
The $j$-th line, at first, contains the integer $t_j$ ($1 \le t_j \le 3$) — the type of query.
If the query is of type $t_j = 1$ or $t_j = 2$, then the integer $k_j$ ($1 \le k_j \le n$) — the length of the shift — follows in the same line.
OutputOutput $q + 1$ numbers — the minimum number of carriage resets required before and after each of Polycarp's queries.
ExamplesInput3 2 3 1 0Output
1Input
3 1 2 3 2 2 1 3Output
0 2 1Input
5 3 1 2 5 4 5 1 3 3 2 3 1 4 3Output
3 2 1 2 1 2Note
In the first example, the answer is $1$. You can understand how the carriage works using this example.

In the second example, the sequences for which the answer needs to be calculated look like this:
- Before all queries: $1\ 2\ 3$ — the answer is $0$.
- After shifting to the right by $1$: $3\ 1\ 2$ — the answer is $2$.
- After reversing the sequence: $2\ 1\ 3$ — the answer is $1$.
In the third example, the sequences before and after each query look like this:
- $3\ 1\ 2\ 5\ 4$ — the answer is $3$.
- $5\ 4\ 3\ 1\ 2$ — the answer is $2$.
- $2\ 1\ 3\ 4\ 5$ — the answer is $1$.
- $3\ 4\ 5\ 2\ 1$ — the answer is $2$.
- $1\ 3\ 4\ 5\ 2$ — the answer is $1$.
- $2\ 5\ 4\ 3\ 1$ — the answer is $2$.
Input
题意翻译
# 打字机 ## 题目描述 最近,Polycarp收到了一台特殊的打字机作为礼物!不幸的是,这台打字机有一个相当奇怪的设计。 这台打字机由 $n$ 个单元组成,从左到右编号为 $1$ 到 $n$ ,还有一个移动的小车。打字机的每个单元包含 $n$ 个不同的整数,从 $1$ 到 $n$ ,每个单元 $i$ 最初包含整数 $p_i$ 。在所有操作之前,小车位于第一个单元上,它的缓冲区没有任何内容。当前小车所在的单元称为当前单元。 小车可以执行以下五种操作: - 如果当前单元不为空,就将其中的整数放入小车的缓冲区(缓冲区最多只能容纳一个整数)。 - 如果小车的缓冲区不为空,就将其中的整数放入当前单元(如果当前单元为空)。 - 如果小车的缓冲区和当前单元都含有整数,就交换缓冲区中的整数和当前单元中的整数。 - 将小车从当前单元 $i$ 移动到下一个单元 $i+1$ (如果 $i<n$ ),缓冲区中的整数保持不变。 - 将小车重置,即将其移动到第一个单元,缓冲区中的整数保持不变。 Polycarp对这个打字机非常感兴趣,所以他请你帮助他理解它,并回答他 $q$ 个问题: 1. 执行一个循环左移 $k_j$ 的操作。 2. 执行一个循环右移 $k_j$ 的操作。 3. 反转序列。 在每个查询之前和之后,Polycarp想要知道为了将数字分配到它们的单元(使数字 $i$ 最终位于第 $i$ 个单元),需要多少次小车重置的最小次数。 注意,Polycarp只想知道需要多少次小车重置来整理数字的位置,但实际上并不进行分配。 帮助Polycarp找到每个查询的答案! ## 输入格式 第一行包含一个整数 $n$ ( $1 \le n \le 4 \cdot 10^5$ )——单元的数量。 第二行包含 $n$ 个不同的整数 $p_1, p_2, \ldots, p_n$ ( $1 \le p_i \le n$ )——单元中整数的初始排列。 第三行包含一个整数 $q$ ( $0 \le q \le 4 \cdot 10^5$ )——Polycarp提出的查询数量。 接下来的 $q$ 行描述了Polycarp的查询: 第 $j$ 行首先包含整数 $t_j$ ( $1 \le t_j \le 3$ )——查询的类型。 如果查询的类型是 $t_j = 1$ 或 $t_j = 2$ ,则在同一行中还会跟着整数 $k_j$ ( $1 \le k_j \le n$ )——移动的长度。 ## 输出格式 输出 $q+1$ 个整数——在每个Polycarp的查询之前和之后,需要进行小车重置的最小次数。 ## 样例 #1 ### 样例输入 #1 ``` 3 2 3 1 0 ``` ### 样例输出 #1 ``` 1 ``` ## 样例 #2 ### 样例输入 #2 ``` 3 1 2 3 2 2 1 3 ``` ### 样例输出 #2 ``` 0 2 1 ``` ## 样例 #3 ### 样例输入 #3 ``` 5 3 1 2 5 4 5 1 3 3 2 3 1 4 3 ``` ### 样例输出 #3 ``` 3 2 1 2 1 2 ``` ## 提示 在第一个示例中,答案为 $1$ 。你可以通过这个示例了解小车的工作方式。 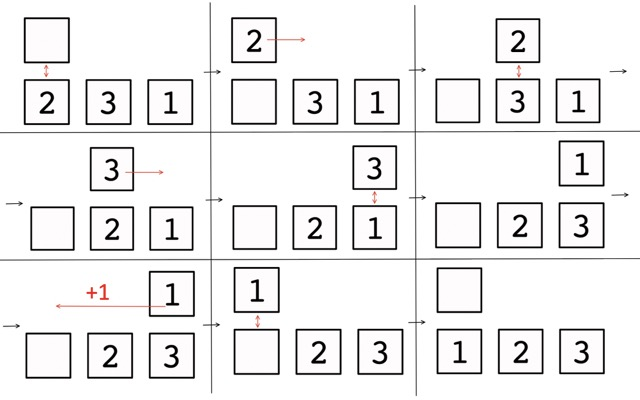在第二个示例中,需要计算答案的序列如下: 1. 所有查询之前:$1\ 2\ 3$ —— 答案为 $0$ 。 2. 右移 $1$ 位之后:$3\ 1\ 2$ —— 答案为 $2$ 。 3. 反转序列之后:$2\ 1\ 3$ —— 答案为 $1$ 。 在第三个示例中,每个查询之前和之后的序列如下: 1. $3\ 1\ 2\ 5\ 4$ —— 答案为 $3$ 。 2. $5\ 4\ 3\ 1\ 2$ —— 答案为 $2$ 。 3. $2\ 1\ 3\ 4\ 5$ —— 答案为 $1$ 。 4. $3\ 4\ 5\ 2\ 1$ —— 答案为 $2$ 。 5. $1\ 3\ 4\ 5\ 2$ —— 答案为 $1$ 。 6. $2\ 5\ 4\ 3\ 1$ —— 答案为 $2$ 。Output
Polycarp收到了一台有缺陷的打字机作为礼物,这台打字机有n个从1到n编号的单元格,每个单元格初始包含一个不同的整数p_i。打字机可以执行五种操作:从当前单元格取整数放入缓冲区、从缓冲区取整数放入当前单元格、交换缓冲区和当前单元格的整数、向右移动一个单元格、重置到第一个单元格。Polycarp会询问q个问题,包括对序列p进行左移、右移或反转。每次询问前后,需要计算将整数分配到其单元格所需的最小重置次数。
输入数据格式:
第一行:一个整数n (1 ≤ n ≤ 4 × 10^5),表示单元格数量。
第二行:n个不同的整数p_1, p_2, ..., p_n (1 ≤ p_i ≤ n),表示初始序列。
第三行:一个整数q (0 ≤ q ≤ 4 × 10^5),表示询问数量。
接下来q行:每行描述一个询问,首先是一个整数t_j (1 ≤ t_j ≤ 3),表示询问类型,如果t_j为1或2,则接下来是一个整数k_j (1 ≤ k_j ≤ n),表示移动的长度。
输出数据格式:
输出q+1个整数,分别表示每次询问前后所需的最小重置次数。题目大意: Polycarp收到了一台有缺陷的打字机作为礼物,这台打字机有n个从1到n编号的单元格,每个单元格初始包含一个不同的整数p_i。打字机可以执行五种操作:从当前单元格取整数放入缓冲区、从缓冲区取整数放入当前单元格、交换缓冲区和当前单元格的整数、向右移动一个单元格、重置到第一个单元格。Polycarp会询问q个问题,包括对序列p进行左移、右移或反转。每次询问前后,需要计算将整数分配到其单元格所需的最小重置次数。 输入数据格式: 第一行:一个整数n (1 ≤ n ≤ 4 × 10^5),表示单元格数量。 第二行:n个不同的整数p_1, p_2, ..., p_n (1 ≤ p_i ≤ n),表示初始序列。 第三行:一个整数q (0 ≤ q ≤ 4 × 10^5),表示询问数量。 接下来q行:每行描述一个询问,首先是一个整数t_j (1 ≤ t_j ≤ 3),表示询问类型,如果t_j为1或2,则接下来是一个整数k_j (1 ≤ k_j ≤ n),表示移动的长度。 输出数据格式: 输出q+1个整数,分别表示每次询问前后所需的最小重置次数。