310468: CF1838D. Bracket Walk

D. Bracket Walktime limit per test3 secondsmemory limit per test256 megabytesinputstandard inputoutputstandard output

There is a string $s$ of length $n$ consisting of the characters '(' and ')'. You are walking on this string. You start by standing on top of the first character of $s$, and you want to make a sequence of moves such that you end on the $n$-th character. In one step, you can move one space to the left (if you are not standing on the first character), or one space to the right (if you are not standing on the last character). You may not stay in the same place, however you may visit any character, including the first and last character, any number of times.

At each point in time, you write down the character you are currently standing on. We say the string is walkable if there exists some sequence of moves that take you from the first character to the last character, such that the string you write down is a regular bracket sequence.

A regular bracket sequence is a bracket sequence that can be transformed into a correct arithmetic expression by inserting characters '1' and '+' between the original characters of the sequence. For example, bracket sequences "()()", "(())" are regular (the resulting expressions are: "(1)+(1)", "((1+1)+1)"), and ")(" and "(" are not.

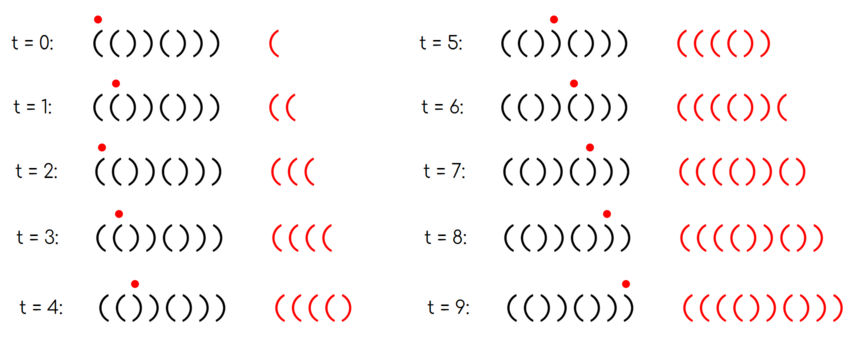One possible valid walk on $s=\mathtt{(())()))}$. The red dot indicates your current position, and the red string indicates the string you have written down. Note that the red string is a regular bracket sequence at the end of the process.

You are given $q$ queries. Each query flips the value of a character from '(' to ')' or vice versa. After each query, determine whether the string is walkable.

Queries are cumulative, so the effects of each query carry on to future queries.

Input

The first line of the input contains two integers $n$ and $q$ ($1 \le n, q \le 2\cdot 10^5$) — the size of the string and the number of queries, respectively.

The second line of the input contains a string $s$ of size $n$, consisting of the characters '(' and ')' — the initial bracket string.

Each of the next $q$ lines contains a single integer $i$ ($1\le i \le n$) — the index of the character to flip for that query.

Output

For each query, print "YES" if the string is walkable after that query, and "NO" otherwise.

You can output the answer in any case (upper or lower). For example, the strings "yEs", "yes", "Yes", and "YES" will be recognized as positive responses.

ExamplesInput

10 9
(())()()))
9
7
2
6
3
6
7
4
8

Output

YES
YES
NO
NO
YES
NO
YES
NO
NO

Input

3 2
(()
2
3

Output

NO
NO

Note

In the first example:

• After the first query, the string is (())()()(). This string is a regular bracket sequence, so it is walkable by simply moving to the right.
• After the second query, the string is (())()))(). If you move right once, then left once, then walk right until you hit the end of the string, you produce the string (((())()))(), which is a regular bracket sequence.
• After the third query, the string is ()))()))(). We can show that this string is not walkable.

In the second example, the strings after the queries are ()) and ()(, neither of which are walkable.

题目大意：
给定一个由字符 '(' 和 ')' 组成的字符串 s，长度为 n。你从字符串的第一个字符开始，通过一系列移动，目的是到达第 n 个字符。每次移动可以向左或向右移动一个位置，但不能停留在原地。在移动过程中，记录下每次移动后所在位置的字符。如果存在某种移动序列，使得记录下的字符串是一个合法的括号序列，则称该字符串是“可走的”。

一个合法的括号序列是指可以通过在原序列的字符之间插入 '1' 和 '+' 来形成一个正确的算术表达式。例如，"()()" 和 "(())" 是合法的，而 ")((" 和 "(" 不是。

题目包含 q 个查询，每个查询会翻转字符串中的一个字符（'(' 变 ')' 或 ')' 变 '('）。在每次查询后，需要判断字符串是否是“可走的”。

输入输出数据格式：
输入：
- 第一行包含两个整数 n 和 q，分别表示字符串的长度和查询的数量。
- 第二行包含一个长度为 n 的字符串 s，由 '(' 和 ')' 组成。
- 接下来的 q 行，每行包含一个整数 i，表示要翻转的字符的位置。

输出：
- 对于每个查询，如果字符串是“可走的”，输出 "YES"，否则输出 "NO"。

示例：
输入：
```
10 9
(())()()))
9
7
2
6
3
6
7
4
8
```
输出：
```
YES
YES
NO
NO
YES
NO
YES
NO
NO
```

注意：
- 在第一个示例中，第一次查询后字符串变为 "(())()()()"，是一个合法的括号序列，因此是可走的。第二次查询后字符串变为 "(())()))()"，可以通过特定的移动形成合法的括号序列。第三次查询后字符串变为 "))()))()"，无法通过任何移动形成合法的括号序列。
- 在第二个示例中，查询后的字符串 "())" 和 "()( " 都不是合法的括号序列。题目大意： 给定一个由字符 '(' 和 ')' 组成的字符串 s，长度为 n。你从字符串的第一个字符开始，通过一系列移动，目的是到达第 n 个字符。每次移动可以向左或向右移动一个位置，但不能停留在原地。在移动过程中，记录下每次移动后所在位置的字符。如果存在某种移动序列，使得记录下的字符串是一个合法的括号序列，则称该字符串是“可走的”。 一个合法的括号序列是指可以通过在原序列的字符之间插入 '1' 和 '+' 来形成一个正确的算术表达式。例如，"()()" 和 "(())" 是合法的，而 ")((" 和 "(" 不是。 题目包含 q 个查询，每个查询会翻转字符串中的一个字符（'(' 变 ')' 或 ')' 变 '('）。在每次查询后，需要判断字符串是否是“可走的”。 输入输出数据格式： 输入： - 第一行包含两个整数 n 和 q，分别表示字符串的长度和查询的数量。 - 第二行包含一个长度为 n 的字符串 s，由 '(' 和 ')' 组成。 - 接下来的 q 行，每行包含一个整数 i，表示要翻转的字符的位置。 输出： - 对于每个查询，如果字符串是“可走的”，输出 "YES"，否则输出 "NO"。 示例： 输入： ``` 10 9 (())()())) 9 7 2 6 3 6 7 4 8 ``` 输出： ``` YES YES NO NO YES NO YES NO NO ``` 注意： - 在第一个示例中，第一次查询后字符串变为 "(())()()()"，是一个合法的括号序列，因此是可走的。第二次查询后字符串变为 "(())()))()"，可以通过特定的移动形成合法的括号序列。第三次查询后字符串变为 "))()))()"，无法通过任何移动形成合法的括号序列。 - 在第二个示例中，查询后的字符串 "())" 和 "()( " 都不是合法的括号序列。